2021-2022学年人教版数学八年级下册第17章勾股定理复习课件 (共19张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册第17章勾股定理复习课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 12:57:44 | ||
图片预览



文档简介
(共19张PPT)
勾股定理复习巩固
学习目标
1. 熟练掌握勾股定理及其逆定理的应用.
2.理解并掌握勾股定理与其他知识的综合应用.
题型一.折叠图形中勾股定理的运用
例1. 如图,小强用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为10cm,长AC为8cm ,当小红折叠时,顶点D落在边AB上的点F处(折痕为CE).算一算,此时BE有多长?
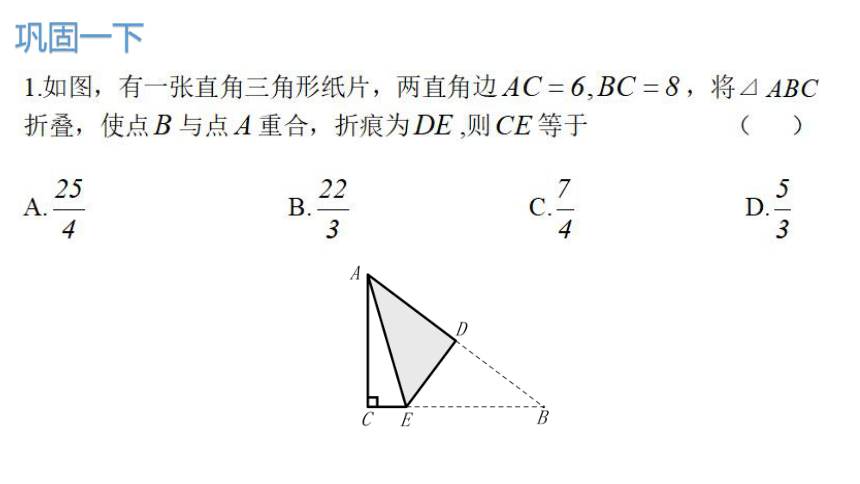
巩固一下
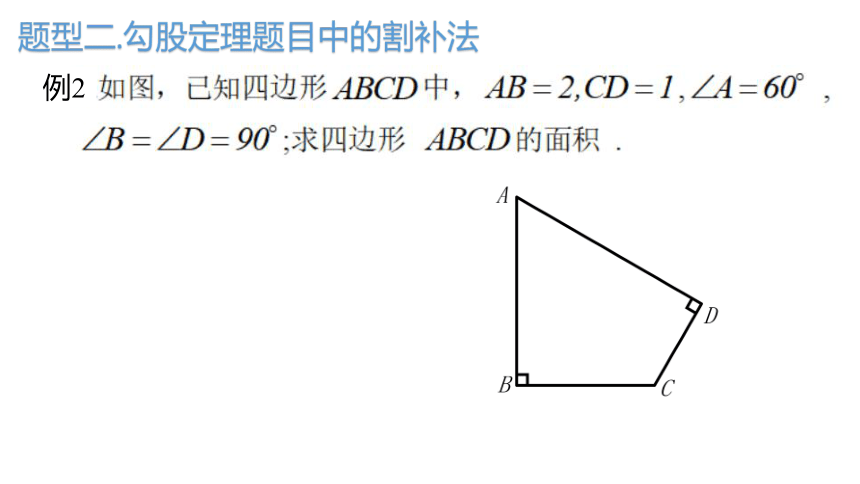
题型二.勾股定理题目中的割补法
例2
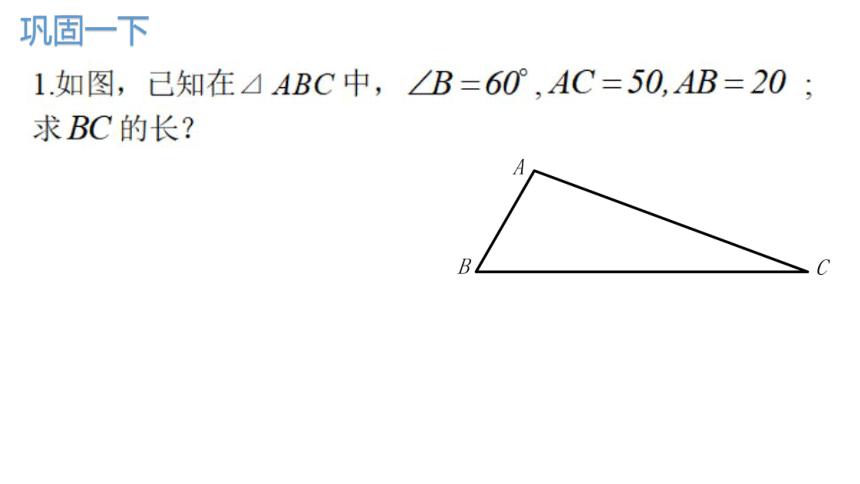
巩固一下
题型三. 网格图形中的勾股定理
解:
巩固一下
题型四.求最短路径中的勾股定理
巩固一下
题型五 利用勾股定理解决几何表面的最短路径问题
例5 如图,有一个圆柱,它的高为12cm,底面半径为3cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面B点处的食物,则需要爬行的最短路程是多少cm?(π的值取3)
C
化曲为直
解:由题可知,BC的长是圆柱底面周长的一半,AC是圆柱的高
∴BC= ×2πr = ×2×3×3=9, AC=12
∵ Rt△ABC中,BC=9,AC=12
∴
C
化曲为直
变式应用:
如图所示,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处,问怎样走路线最短?最短路线长为多少?
【分析】蚂蚁由A点沿长方体的表面爬行到C1点,有三种方式:
①沿ABB1A1和A1 B1C1D1面;②沿ABB1A1和BCC1B1面;③沿AA1D1D和A1B1C1D1面,把三种方式分别展成平面图形如下:
巩固一下
勾股定理复习巩固
学习目标
1. 熟练掌握勾股定理及其逆定理的应用.
2.理解并掌握勾股定理与其他知识的综合应用.
题型一.折叠图形中勾股定理的运用
例1. 如图,小强用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为10cm,长AC为8cm ,当小红折叠时,顶点D落在边AB上的点F处(折痕为CE).算一算,此时BE有多长?
巩固一下
题型二.勾股定理题目中的割补法
例2
巩固一下
题型三. 网格图形中的勾股定理
解:
巩固一下
题型四.求最短路径中的勾股定理
巩固一下
题型五 利用勾股定理解决几何表面的最短路径问题
例5 如图,有一个圆柱,它的高为12cm,底面半径为3cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面B点处的食物,则需要爬行的最短路程是多少cm?(π的值取3)
C
化曲为直
解:由题可知,BC的长是圆柱底面周长的一半,AC是圆柱的高
∴BC= ×2πr = ×2×3×3=9, AC=12
∵ Rt△ABC中,BC=9,AC=12
∴
C
化曲为直
变式应用:
如图所示,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处,问怎样走路线最短?最短路线长为多少?
【分析】蚂蚁由A点沿长方体的表面爬行到C1点,有三种方式:
①沿ABB1A1和A1 B1C1D1面;②沿ABB1A1和BCC1B1面;③沿AA1D1D和A1B1C1D1面,把三种方式分别展成平面图形如下:
巩固一下
