华东师大版七年级下册数学 8.3 一元一次不等式组课件 (共21张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 8.3 一元一次不等式组课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
8.3 一元一次不等式组
1.了解一元一次不等式组及其解集的概念;
2.会解一元一次不等式组,能用数轴表示不等式组的解集,初步领会数形结合的思想.
学习目标
用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水不少于1200吨且不多于1500吨,那么需要多少分钟能将污水抽完?
把两个一元一次不等式合起来,就组成一个一元一次不等式组.
分析:设需要x分钟能将污水抽完. 30x≥1200 并且 30x≤1500
问题
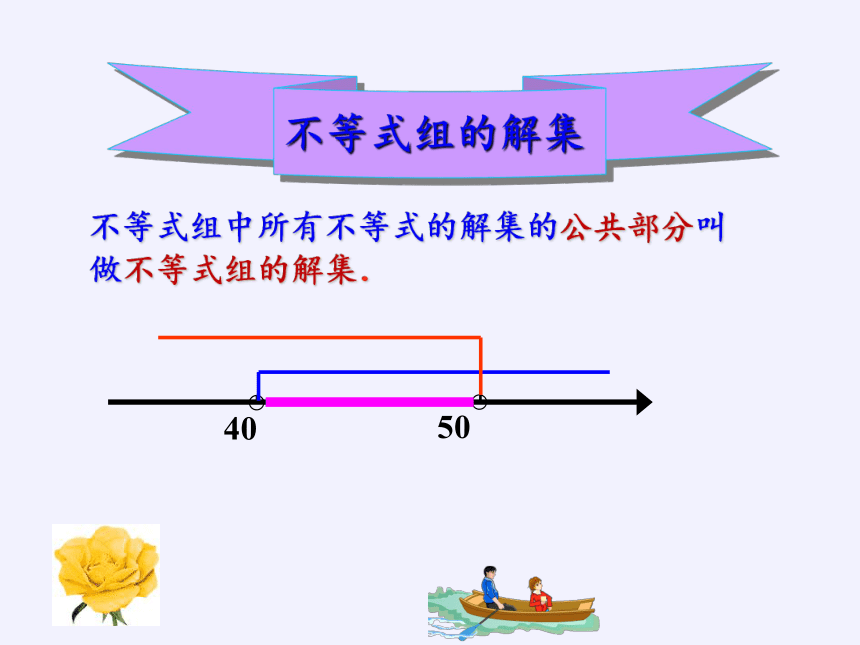
不等式组的解集
分别求这两个不等式的解集,得
同时满足不等式①、②的未知数x应是这两个不等式解集的公共部分,如图
40
50
不等式组中所有不等式的解集的公共部分叫做不等式组的解集.
不等式组的解集
40
50
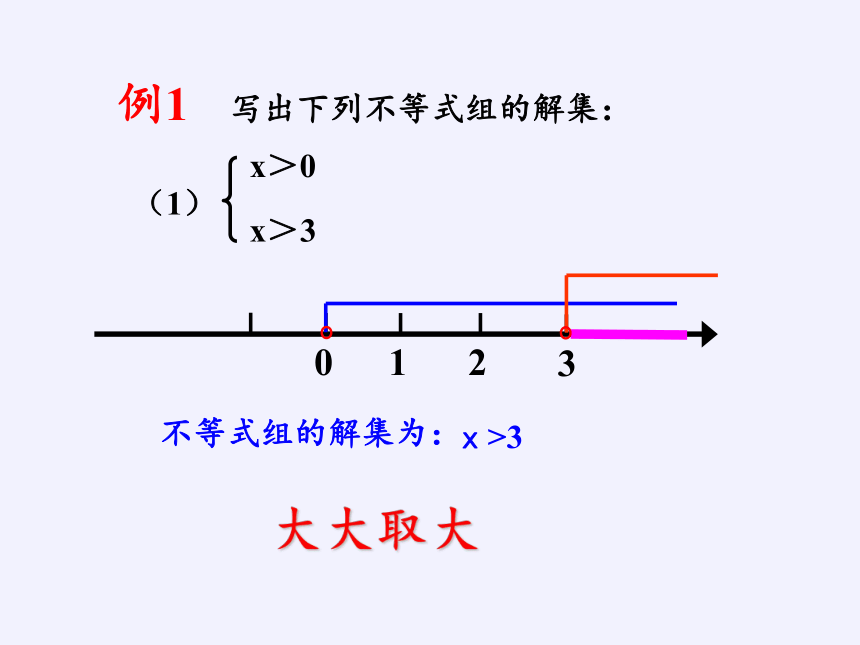
不等式组的解集为:
x>3
大大取大
x>3
x>0
(1)
2
1
3
0
例1 写出下列不等式组的解集:
2
1
3
0
不等式组的解集为:
x<0
x<3
x<0
(2)
小小取小
2
1
3
0
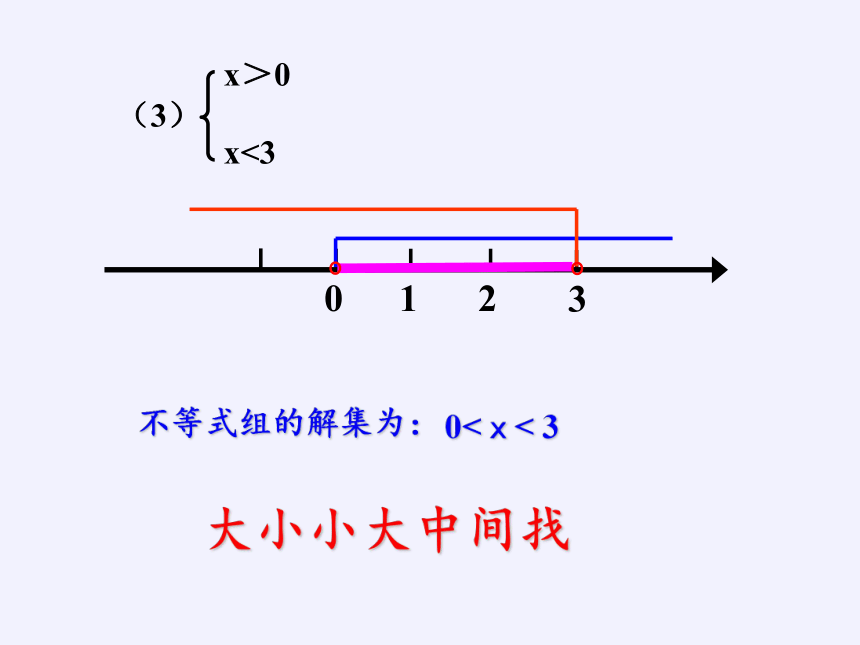
不等式组的解集为:
0<x< 3
x<3
x>0
(3)
大小小大中间找
2
1
3
0
不等式组无解
大大小小解不了
练习 利用数轴,确定下列各不等式组的解集:
解:
-3
-2
-1
0
1
2
.
·
·
不等式组的解集是 -1≤x<2.
解:
-3
-2
-1
0
1
2
.
.
不等式组的解集是 x>1.
解:
-3
-2
-1
0
1
2
.
·
不等式组的解集是 x≤-2.
解:
- 3
-2
-1
0
1
2
.
.
不等式组无解.
40
50
在同一数轴上表示不等式①和②的解集.
例2 解不等式组:
解:解不等式①,得 x≥40
解不等式②,得 x≤50
这个不等式的解集为 40≤x≤50
解一元一次不等式组的一般步骤
(1)求出每个不等式的解集;
(2)把不等式的解集在同一个数轴上表示出来;
(3)找出各个不等式的解集的公共部分;
(4)不等式组的解集就是这个公共部分.
6
5
解:解不等式①,得x>6
解不等式②,得x>5
不等式组的解集是:x>6.
把不等式①和②的解在数轴上表示出来.
练习 解不等式组:
5x-3>3(x+3)
3 x-4 >2x+1
①
②
-5
-7
解:解不等式① ,得
解不等式② ,得
x <-7
x >-5
所以,原不等式组无解.
练习 解不等式组
3 (x+1) <2x-4
2(x-2)<3x+1
①
②
把不等式①和②的解在数轴上表示出来.
例3 求不等式组的整数解
2x-5≤5(x+2) ①
3x+2≤x-7 ②
所以,不等式的整数解为-5,-4,-3.
-5
解:解不等式① ,得x≥-5
解不等式② ,得 x≤
所以,不等式的解集为
(1)求出每个不等式的解集
(2)把不等式的解集在同一个数轴上表示出来;
(3)找出各个不等式的解集的公共部分;
(大大取大,小小取小,大小小大中间找,大大小小找不了.)
(4)不等式组的解集就是这个公共部分.
温馨提示:没有公共部分称为不等式组无解.
解一元一次不等式组的步骤:
课堂小结
1.使不等式x+6≥0与2x-4<0都成立的x的取值范
围是__________.
2.不等式-1≤2x-1≤5的解集是_________.
-6≤x<2
0≤x≤3
1、2、3
反馈检测
x+2>0
2x-3<5
3.不等式组 的正整数解是_________.
解:解不等式①,得,
x>2
解不等式②,得,
x>2
⑴
②
①
⑵
②
①
所以不等式组的解集:x>2.
解: 解不等式①,得,
x≥8
解不等式②,得,
x<0
所以不等式组无解.
4.解下列不等式组
5.若不等式组 无解,则m的取值范
围是________.
x<m+2
x>2m-1
m≥3
谢 谢
8.3 一元一次不等式组
1.了解一元一次不等式组及其解集的概念;
2.会解一元一次不等式组,能用数轴表示不等式组的解集,初步领会数形结合的思想.
学习目标
用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水不少于1200吨且不多于1500吨,那么需要多少分钟能将污水抽完?
把两个一元一次不等式合起来,就组成一个一元一次不等式组.
分析:设需要x分钟能将污水抽完. 30x≥1200 并且 30x≤1500
问题
不等式组的解集
分别求这两个不等式的解集,得
同时满足不等式①、②的未知数x应是这两个不等式解集的公共部分,如图
40
50
不等式组中所有不等式的解集的公共部分叫做不等式组的解集.
不等式组的解集
40
50
不等式组的解集为:
x>3
大大取大
x>3
x>0
(1)
2
1
3
0
例1 写出下列不等式组的解集:
2
1
3
0
不等式组的解集为:
x<0
x<3
x<0
(2)
小小取小
2
1
3
0
不等式组的解集为:
0<x< 3
x<3
x>0
(3)
大小小大中间找
2
1
3
0
不等式组无解
大大小小解不了
练习 利用数轴,确定下列各不等式组的解集:
解:
-3
-2
-1
0
1
2
.
·
·
不等式组的解集是 -1≤x<2.
解:
-3
-2
-1
0
1
2
.
.
不等式组的解集是 x>1.
解:
-3
-2
-1
0
1
2
.
·
不等式组的解集是 x≤-2.
解:
- 3
-2
-1
0
1
2
.
.
不等式组无解.
40
50
在同一数轴上表示不等式①和②的解集.
例2 解不等式组:
解:解不等式①,得 x≥40
解不等式②,得 x≤50
这个不等式的解集为 40≤x≤50
解一元一次不等式组的一般步骤
(1)求出每个不等式的解集;
(2)把不等式的解集在同一个数轴上表示出来;
(3)找出各个不等式的解集的公共部分;
(4)不等式组的解集就是这个公共部分.
6
5
解:解不等式①,得x>6
解不等式②,得x>5
不等式组的解集是:x>6.
把不等式①和②的解在数轴上表示出来.
练习 解不等式组:
5x-3>3(x+3)
3 x-4 >2x+1
①
②
-5
-7
解:解不等式① ,得
解不等式② ,得
x <-7
x >-5
所以,原不等式组无解.
练习 解不等式组
3 (x+1) <2x-4
2(x-2)<3x+1
①
②
把不等式①和②的解在数轴上表示出来.
例3 求不等式组的整数解
2x-5≤5(x+2) ①
3x+2≤x-7 ②
所以,不等式的整数解为-5,-4,-3.
-5
解:解不等式① ,得x≥-5
解不等式② ,得 x≤
所以,不等式的解集为
(1)求出每个不等式的解集
(2)把不等式的解集在同一个数轴上表示出来;
(3)找出各个不等式的解集的公共部分;
(大大取大,小小取小,大小小大中间找,大大小小找不了.)
(4)不等式组的解集就是这个公共部分.
温馨提示:没有公共部分称为不等式组无解.
解一元一次不等式组的步骤:
课堂小结
1.使不等式x+6≥0与2x-4<0都成立的x的取值范
围是__________.
2.不等式-1≤2x-1≤5的解集是_________.
-6≤x<2
0≤x≤3
1、2、3
反馈检测
x+2>0
2x-3<5
3.不等式组 的正整数解是_________.
解:解不等式①,得,
x>2
解不等式②,得,
x>2
⑴
②
①
⑵
②
①
所以不等式组的解集:x>2.
解: 解不等式①,得,
x≥8
解不等式②,得,
x<0
所以不等式组无解.
4.解下列不等式组
5.若不等式组 无解,则m的取值范
围是________.
x<m+2
x>2m-1
m≥3
谢 谢
