华东师大版七年级下册数学 8.2 一元一次不等式的解法 课件(共13张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 8.2 一元一次不等式的解法 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 14:06:59 | ||
图片预览





文档简介
(共13张PPT)
§13.3.3
解一元一次不等式(3)
一. 知识回顾
1.不等式:
注意:此时不等号方向改变!
2.不等式的性质:
3.一元一次不等式:
4.一元一次不等式的一般形式:
表示不等关系的式子叫不等式。
①若a < b,则 a + c < b + c, a-c < b - c;
②若a < b, c > 0,则 a c < b c ;
③若a < b, c < 0,则 a c > b c .
如果不等式中只含有一个未知数,且含未知数的式子是整式,未知数的次数是1,这样的不等式叫做一元一次不等式.
二.复习练习
解不等式:
(1) +1>x; (2)3(1-x)-2(x+8)<2;
(3) - >-2.
解不等式:
(1) +1>x; (2)3(1-x)-2(x+8)<2;
(-2) ×(- )< -1×(-2)
解: 3 – 3x – 2x – 16 <2
注意:此时不等号方向改变!
注意:此时不等号方向改变!
解: - x > -1
- > -1
x < 2 .
x > –3 .
– 5x ÷ ( – 5)> 15 ÷ ( – 5)
– 5x < 15
– 3x – 2x < 2 – 3 + 16
解不等式:
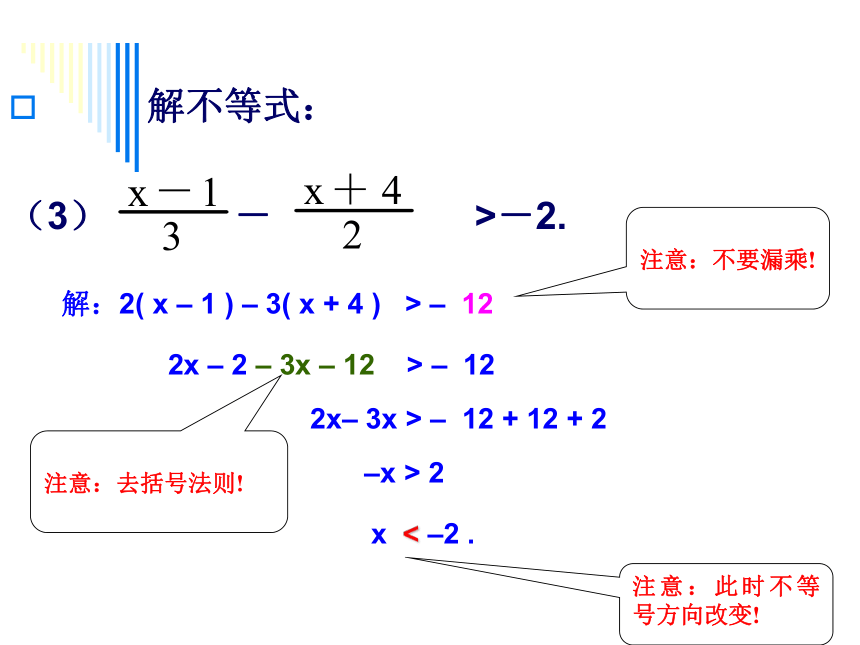
(3) - >-2.
解:2( x – 1 ) – 3( x + 4 ) > – 12
注意:此时不等号方向改变!
注意:不要漏乘!
注意:去括号法则!
2x – 2 – 3x – 12 > – 12
2x– 3x > – 12 + 12 + 2
–x > 2
x < –2 .
三. 新课
问题1.求不等式 >-3
的自然数解.
解:解原不等式得 2(x - 3) -(6x - 1) > -18
2x - 6 - 6x + 1 > -18
2x - 6x > -18 + 6 - 1
- 4x > - 13
x < .
∴原不等式的自然数解是0,1,2,3。
问题2.当x取何值时,代数式 的值比
的值大1?
解 根据题意,得
-
>1
2(x+4)-3(3x-1)>6
2x+8-9x+3>6
-7x+11>6
-7x>-5
x<
∴当 时,代数式 的值比 的值大1。
x<
问题3.在“科学与艺术”知识竞赛的预选赛中共
有20道题,对于每一道题,答对得10分,答错或不答扣5分,总得分不少于80分者通过预选赛.育才中学25名学生通过了预选赛,他们分别可能答对了多少道题
试解决这个问题(不限定方法)
有没有其他方法?与你的同伴讨论和交流一下。
解:设答对了x道题,根据题意得
10x-5(20-x)≥ 80
解得 x ≥ 12.
∴ 他们分别可能答对了12,13,14,
15,16,17,18,19,20道题。
练习一:一个工程队原定在10天内至少要挖土600m3,在前两天一共完成了120 m3,由于整个工程调整工期,要求提前两天完成挖土任务。问以后几天内,平均每天至少要挖土多少m3?
练习二:王老师在一次数学竞赛中共出了25道题,
规定答对一题得4分,答错或不答—道题扣1分,在
这次竞赛中,小明被评为达标(60分或60分以上)。
小明可能答对几道题
练习三:某校准备组织学生去外地参加夏令营活动,车
站提出两种车票价格的优惠方案:第一种方案是教师按
原价付款,学生按原价的78%付款;第二种方案是师生
都按原价的80%付款.该校有5名教师参加这项活动,试
根据夏令营学生人数选择购票的最佳方案.
练习一:一个工程队原定在10天内至少要挖土600m3,在前两天一共完成了120 m3,由于整个工程调整工期,要求提前两天完成挖土任务。问以后几天内,平均每天至少要挖土多少m3?
解:设以后几天内平均每天挖土xm3,根据题意得
答:以后几天内,平均每天至少要挖土80m3 。
6x+120≥ 600
解得 x ≥80.
练习二:王老师在一次数学竞赛中共出了25道题,
规定答对一题得4分,答错或不答—道题扣
1分,在这次竞赛中,小明被评为达标(60
分或60分以上)。小明可能答对几道题
解:设小明答对了x道题,根据题意得
∴小明可能答对了17,18,19,
20,21,22,23,24,25道题。
4x-(25-x)≥ 60
解得 x ≥ 17.
解:设该校参加夏令营的学生有x人,车票原价a元,根据题意得
第一种优惠方案需付款 (5a+78%ax)元
第二种优惠方案需付款80%a(5+x)元
练习三:某校准备组织学生去外地参加夏令营活动,车
站提出两种车票价格的优惠方案:第一种方案是教师按
原价付款,学生按原价的78%付款;第二种方案是师生
都按原价的80%付款.该校有5名教师参加这项活动,试
根据夏令营学生人数选择购票的最佳方案.
①当5a+78%ax> 80%a(5+x)时,
②当5a+78%ax< 80%a(5+x)时,
③当5a+78%ax= 80%a(5+x)时,
解得 x < 50.
∴当学生人数少于50人时,选择第二种付款方案好。
解得 x > 50.
∴当学生人数大于50人时,选择第一种付款方案好。
解得 x = 50.
∴当学生人数为50人时,两种方案付款一样多。
§13.3.3
解一元一次不等式(3)
一. 知识回顾
1.不等式:
注意:此时不等号方向改变!
2.不等式的性质:
3.一元一次不等式:
4.一元一次不等式的一般形式:
表示不等关系的式子叫不等式。
①若a < b,则 a + c < b + c, a-c < b - c;
②若a < b, c > 0,则 a c < b c ;
③若a < b, c < 0,则 a c > b c .
如果不等式中只含有一个未知数,且含未知数的式子是整式,未知数的次数是1,这样的不等式叫做一元一次不等式.
二.复习练习
解不等式:
(1) +1>x; (2)3(1-x)-2(x+8)<2;
(3) - >-2.
解不等式:
(1) +1>x; (2)3(1-x)-2(x+8)<2;
(-2) ×(- )< -1×(-2)
解: 3 – 3x – 2x – 16 <2
注意:此时不等号方向改变!
注意:此时不等号方向改变!
解: - x > -1
- > -1
x < 2 .
x > –3 .
– 5x ÷ ( – 5)> 15 ÷ ( – 5)
– 5x < 15
– 3x – 2x < 2 – 3 + 16
解不等式:
(3) - >-2.
解:2( x – 1 ) – 3( x + 4 ) > – 12
注意:此时不等号方向改变!
注意:不要漏乘!
注意:去括号法则!
2x – 2 – 3x – 12 > – 12
2x– 3x > – 12 + 12 + 2
–x > 2
x < –2 .
三. 新课
问题1.求不等式 >-3
的自然数解.
解:解原不等式得 2(x - 3) -(6x - 1) > -18
2x - 6 - 6x + 1 > -18
2x - 6x > -18 + 6 - 1
- 4x > - 13
x < .
∴原不等式的自然数解是0,1,2,3。
问题2.当x取何值时,代数式 的值比
的值大1?
解 根据题意,得
-
>1
2(x+4)-3(3x-1)>6
2x+8-9x+3>6
-7x+11>6
-7x>-5
x<
∴当 时,代数式 的值比 的值大1。
x<
问题3.在“科学与艺术”知识竞赛的预选赛中共
有20道题,对于每一道题,答对得10分,答错或不答扣5分,总得分不少于80分者通过预选赛.育才中学25名学生通过了预选赛,他们分别可能答对了多少道题
试解决这个问题(不限定方法)
有没有其他方法?与你的同伴讨论和交流一下。
解:设答对了x道题,根据题意得
10x-5(20-x)≥ 80
解得 x ≥ 12.
∴ 他们分别可能答对了12,13,14,
15,16,17,18,19,20道题。
练习一:一个工程队原定在10天内至少要挖土600m3,在前两天一共完成了120 m3,由于整个工程调整工期,要求提前两天完成挖土任务。问以后几天内,平均每天至少要挖土多少m3?
练习二:王老师在一次数学竞赛中共出了25道题,
规定答对一题得4分,答错或不答—道题扣1分,在
这次竞赛中,小明被评为达标(60分或60分以上)。
小明可能答对几道题
练习三:某校准备组织学生去外地参加夏令营活动,车
站提出两种车票价格的优惠方案:第一种方案是教师按
原价付款,学生按原价的78%付款;第二种方案是师生
都按原价的80%付款.该校有5名教师参加这项活动,试
根据夏令营学生人数选择购票的最佳方案.
练习一:一个工程队原定在10天内至少要挖土600m3,在前两天一共完成了120 m3,由于整个工程调整工期,要求提前两天完成挖土任务。问以后几天内,平均每天至少要挖土多少m3?
解:设以后几天内平均每天挖土xm3,根据题意得
答:以后几天内,平均每天至少要挖土80m3 。
6x+120≥ 600
解得 x ≥80.
练习二:王老师在一次数学竞赛中共出了25道题,
规定答对一题得4分,答错或不答—道题扣
1分,在这次竞赛中,小明被评为达标(60
分或60分以上)。小明可能答对几道题
解:设小明答对了x道题,根据题意得
∴小明可能答对了17,18,19,
20,21,22,23,24,25道题。
4x-(25-x)≥ 60
解得 x ≥ 17.
解:设该校参加夏令营的学生有x人,车票原价a元,根据题意得
第一种优惠方案需付款 (5a+78%ax)元
第二种优惠方案需付款80%a(5+x)元
练习三:某校准备组织学生去外地参加夏令营活动,车
站提出两种车票价格的优惠方案:第一种方案是教师按
原价付款,学生按原价的78%付款;第二种方案是师生
都按原价的80%付款.该校有5名教师参加这项活动,试
根据夏令营学生人数选择购票的最佳方案.
①当5a+78%ax> 80%a(5+x)时,
②当5a+78%ax< 80%a(5+x)时,
③当5a+78%ax= 80%a(5+x)时,
解得 x < 50.
∴当学生人数少于50人时,选择第二种付款方案好。
解得 x > 50.
∴当学生人数大于50人时,选择第一种付款方案好。
解得 x = 50.
∴当学生人数为50人时,两种方案付款一样多。
