华东师大版七年级下册数学 8.3 一元一次不等式组 教案
文档属性
| 名称 | 华东师大版七年级下册数学 8.3 一元一次不等式组 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 96.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 00:00:00 | ||
图片预览

文档简介
§8.3 一元一次不等式组
教学目标
知识与技能:
1、了解一元一次不等式组及其解集的概念。
2、会利用数轴求不等式组的解集。
过程与方法:
1、培养学生分析实际问题,抽象出数学关系的能力。
2、培养学生初步数学建模的能力。
情感态度价值观:
加深学生对数形结合的作用的理解,让学生体会数学解题的直观性和简洁性的数学美。感受探索的乐趣和成功的体验,使学生养成独立思考的好习惯。
教学重难点
重点:不等式组的解法及其步骤。
难点:确定两个不等式解集的公共部分。
教法与学法分析
教法:启发式、讨论式和讲练结合的教学方法。
学法:实践、比较、探究的学习方式。
教学课型
新授课
教学用具
多媒体课件
教学过程
一、复习引入
一元一次不等式的解法我们已经全部讲完,现在复习一下前面的内容。
1、不等式的三个基本性质是什么?
2、一元一次不等式的解法是怎样的?
3、解一元一次不等式
(1) () (2) ()
二、讲授新知
教师讲解课本问题3
问题3:用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水不少于1200吨且不超过1500吨,那么大约多少时间能将污水抽完?
题中一共有两种数量关系,讲解时应注意引导学生自主探究发现。
解:设需要分钟才能将污水抽完,那么总的抽水量为吨,由题可知
题中的应同时满足两个不等式,从而引出一元一次不等式组的概念:把两个一元一次不等式合在一起,就得到一个一元一次不等式组。
解之,得
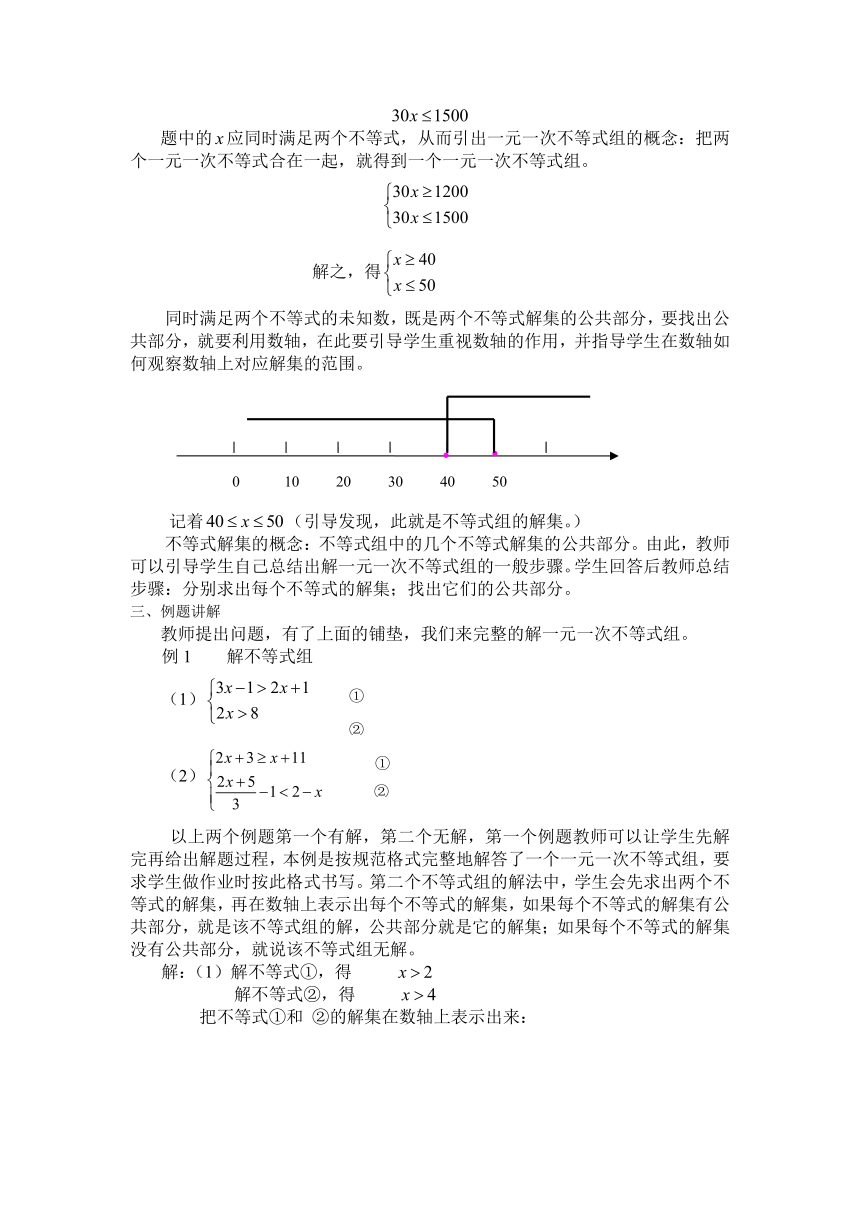
同时满足两个不等式的未知数,既是两个不等式解集的公共部分,要找出公共部分,就要利用数轴,在此要引导学生重视数轴的作用,并指导学生在数轴如何观察数轴上对应解集的范围。
(
0
10
20
30
40
50
)
记着(引导发现,此就是不等式组的解集。)
不等式解集的概念:不等式组中的几个不等式解集的公共部分。由此,教师可以引导学生自己总结出解一元一次不等式组的一般步骤。学生回答后教师总结步骤:分别求出每个不等式的解集;找出它们的公共部分。
三、例题讲解
教师提出问题,有了上面的铺垫,我们来完整的解一元一次不等式组。
例1 解不等式组
(
①
) (
②
)(1)
(
②
) (
①
)(2)
以上两个例题第一个有解,第二个无解,第一个例题教师可以让学生先解完再给出解题过程,本例是按规范格式完整地解答了一个一元一次不等式组,要求学生做作业时按此格式书写。第二个不等式组的解法中,学生会先求出两个不等式的解集,再在数轴上表示出每个不等式的解集,如果每个不等式的解集有公共部分,就是该不等式组的解,公共部分就是它的解集;如果每个不等式的解集没有公共部分,就说该不等式组无解。
解:(1)解不等式①,得
解不等式②,得
把不等式①和 ②的解集在数轴上表示出来:
(
0
1
2
3
4
5
)
则原不等式的解集为
(2)解不等式①,得
解不等式②,得
把不等式①和 ②的解集在数轴上表示出来:
(
0
2
4
6
8
10
)
在这里引导学生发现,没有公共部分,即无解。
四、课堂练习
解下列不等式组,并把他们在数轴上表示出来:、
1、 2、 3、 4、
五、总结升华
设a、b是已知实数且a>b,那么不等式组
表一:不等式组解集
不等式组 数轴表示 解集(即公共部分)
(
b
a
)
(
b
a
)
(
b
a
)
(
b
a
) 无 解
这个表格教师应尽量引导学生自主探究完成,教师最后做出总结:皆大取大,皆小取小,大小小大取中间,大大小小是无解。
六、强化训练
在这里的练习出现了字母,可能有的学生会觉得有字母比较抽象,教师应鼓励学生大胆尝试,同时引导学生利用数轴。
练习:
1、关于的不等式组有解,那么的取值范围是( )
A、 B、 C、 D、
2、如果不等式组的解集是,则 。
3、已知关于关于的不等式组无解,求的取值范围?
七、课时小结
学生学习了一节后有自己的收获,教师应让学生首先总结,教师再做补充。
(一)概念
1、由几个一元一次不等式所组成的不等式组叫做一元一次不等式组。
2、几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集。
3、求不等式组的解集的过程,叫做解不等式组。
(二)解简单一元一次不等式组的方法:
1、求不等式组中各个不等式的解集。
2、利用数轴找出两个不等式的公共部分,即求出了不等式的解集。
八、作业布置
必做:课本习题8.3第一题
选做:1 不等式组的解集是,求的取值范围?
2 当取何值时,方程组中的大于1,小于1?
3 是什么正整数时,方程的解是非负数?
4 关于的不等式组的整数解共有5个,求的取值范围?
板书设计
表二 板书设计表
§8.3 一元一次不等式组
问题3 分析引导 利用数轴 例题讲解 (1)、 (2)、 总结升华 表一 强化训练 练习1 练习2 练习3 作业布置
一元一次不等式组的解集:
(数轴法)同右取右,同左取左,
左右相交取中间、左右相背是无解;
(概念法)大大取较大,小小取较小,
小大,大小取中间,
大小,小大无处找。
教学目标
知识与技能:
1、了解一元一次不等式组及其解集的概念。
2、会利用数轴求不等式组的解集。
过程与方法:
1、培养学生分析实际问题,抽象出数学关系的能力。
2、培养学生初步数学建模的能力。
情感态度价值观:
加深学生对数形结合的作用的理解,让学生体会数学解题的直观性和简洁性的数学美。感受探索的乐趣和成功的体验,使学生养成独立思考的好习惯。
教学重难点
重点:不等式组的解法及其步骤。
难点:确定两个不等式解集的公共部分。
教法与学法分析
教法:启发式、讨论式和讲练结合的教学方法。
学法:实践、比较、探究的学习方式。
教学课型
新授课
教学用具
多媒体课件
教学过程
一、复习引入
一元一次不等式的解法我们已经全部讲完,现在复习一下前面的内容。
1、不等式的三个基本性质是什么?
2、一元一次不等式的解法是怎样的?
3、解一元一次不等式
(1) () (2) ()
二、讲授新知
教师讲解课本问题3
问题3:用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水不少于1200吨且不超过1500吨,那么大约多少时间能将污水抽完?
题中一共有两种数量关系,讲解时应注意引导学生自主探究发现。
解:设需要分钟才能将污水抽完,那么总的抽水量为吨,由题可知
题中的应同时满足两个不等式,从而引出一元一次不等式组的概念:把两个一元一次不等式合在一起,就得到一个一元一次不等式组。
解之,得
同时满足两个不等式的未知数,既是两个不等式解集的公共部分,要找出公共部分,就要利用数轴,在此要引导学生重视数轴的作用,并指导学生在数轴如何观察数轴上对应解集的范围。
(
0
10
20
30
40
50
)
记着(引导发现,此就是不等式组的解集。)
不等式解集的概念:不等式组中的几个不等式解集的公共部分。由此,教师可以引导学生自己总结出解一元一次不等式组的一般步骤。学生回答后教师总结步骤:分别求出每个不等式的解集;找出它们的公共部分。
三、例题讲解
教师提出问题,有了上面的铺垫,我们来完整的解一元一次不等式组。
例1 解不等式组
(
①
) (
②
)(1)
(
②
) (
①
)(2)
以上两个例题第一个有解,第二个无解,第一个例题教师可以让学生先解完再给出解题过程,本例是按规范格式完整地解答了一个一元一次不等式组,要求学生做作业时按此格式书写。第二个不等式组的解法中,学生会先求出两个不等式的解集,再在数轴上表示出每个不等式的解集,如果每个不等式的解集有公共部分,就是该不等式组的解,公共部分就是它的解集;如果每个不等式的解集没有公共部分,就说该不等式组无解。
解:(1)解不等式①,得
解不等式②,得
把不等式①和 ②的解集在数轴上表示出来:
(
0
1
2
3
4
5
)
则原不等式的解集为
(2)解不等式①,得
解不等式②,得
把不等式①和 ②的解集在数轴上表示出来:
(
0
2
4
6
8
10
)
在这里引导学生发现,没有公共部分,即无解。
四、课堂练习
解下列不等式组,并把他们在数轴上表示出来:、
1、 2、 3、 4、
五、总结升华
设a、b是已知实数且a>b,那么不等式组
表一:不等式组解集
不等式组 数轴表示 解集(即公共部分)
(
b
a
)
(
b
a
)
(
b
a
)
(
b
a
) 无 解
这个表格教师应尽量引导学生自主探究完成,教师最后做出总结:皆大取大,皆小取小,大小小大取中间,大大小小是无解。
六、强化训练
在这里的练习出现了字母,可能有的学生会觉得有字母比较抽象,教师应鼓励学生大胆尝试,同时引导学生利用数轴。
练习:
1、关于的不等式组有解,那么的取值范围是( )
A、 B、 C、 D、
2、如果不等式组的解集是,则 。
3、已知关于关于的不等式组无解,求的取值范围?
七、课时小结
学生学习了一节后有自己的收获,教师应让学生首先总结,教师再做补充。
(一)概念
1、由几个一元一次不等式所组成的不等式组叫做一元一次不等式组。
2、几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集。
3、求不等式组的解集的过程,叫做解不等式组。
(二)解简单一元一次不等式组的方法:
1、求不等式组中各个不等式的解集。
2、利用数轴找出两个不等式的公共部分,即求出了不等式的解集。
八、作业布置
必做:课本习题8.3第一题
选做:1 不等式组的解集是,求的取值范围?
2 当取何值时,方程组中的大于1,小于1?
3 是什么正整数时,方程的解是非负数?
4 关于的不等式组的整数解共有5个,求的取值范围?
板书设计
表二 板书设计表
§8.3 一元一次不等式组
问题3 分析引导 利用数轴 例题讲解 (1)、 (2)、 总结升华 表一 强化训练 练习1 练习2 练习3 作业布置
一元一次不等式组的解集:
(数轴法)同右取右,同左取左,
左右相交取中间、左右相背是无解;
(概念法)大大取较大,小小取较小,
小大,大小取中间,
大小,小大无处找。
