安徽省滁州市定远县育才学校2021-2022学年九年级下学期开学考数学试题(word版含答案)
文档属性
| 名称 | 安徽省滁州市定远县育才学校2021-2022学年九年级下学期开学考数学试题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 644.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 00:00:00 | ||
图片预览




文档简介
请务必在“答题卷”上答题,在“试题卷”上答题是无效的
2021-2022学年度第二学期开学考试
九年级数学试题
第I卷(选择题)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列各选项的图形中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
2.如图,已知,若,,,则的长为( )
A.1.5 B.2 C.2.5 D.3
3.将抛物线y=x2先向右平移2个单位长度,再向上平移4个单位长度,得到的新的抛物线的解析式为( )
A.y=(x+2)2+4 B.y=(x+2)2﹣4
C.y=(x﹣2)2+4 D.y=(x﹣2)2﹣4
4.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于点E,AE平分∠BAC,AO=CO,AD=DC=2,下面结论:①AC=2AB;②AB=;③S△ADC=2S△ABE;④BO⊥AE,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
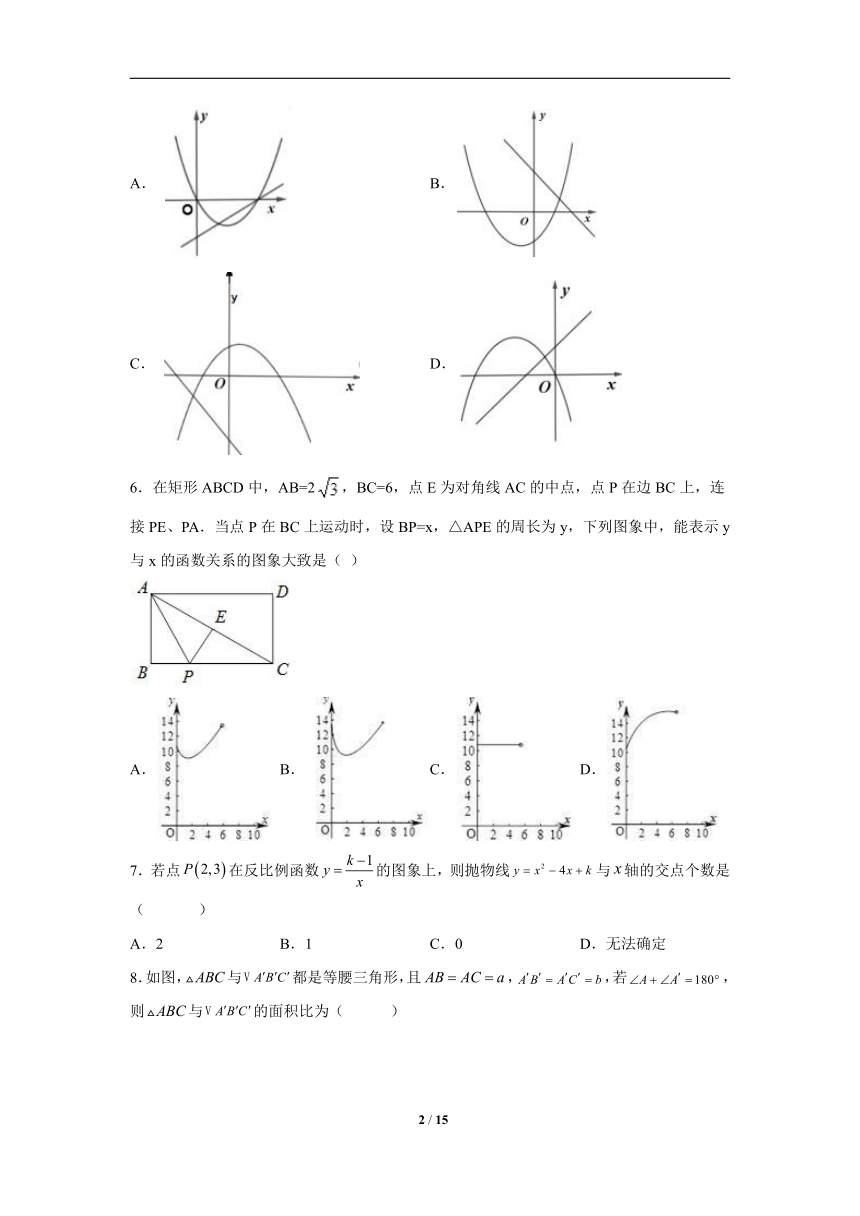
5.在同一平面直角坐标系中,函数与的图象可能是( )
A. B.
C. D.
6.在矩形ABCD中,AB=2,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
7.若点在反比例函数的图象上,则抛物线与轴的交点个数是( )
A.2 B.1 C.0 D.无法确定
8.如图,与都是等腰三角形,且,,若,则与的面积比为( )
A. B. C. D.
9.已知,将如图的三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB.则∠α的余弦值为( )
A. B. C. D.1
10.如图,二次函数的图象经过点,其对称轴为直线,有下列结论:①;②;③;④;⑤若,是抛物线上两点,且,则实数的取值范围是.其中正确结论是( )
A.①③④ B.②④⑤ C.①③⑤ D.①③④⑤
第II卷 非选择题
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知,则的值为_____.
12.如图,菱形的周长为24,对角线与交于点O,,则_________.
13.已知反比例函数(k为常数)在每一象限内,y随x的增大而增大,则k的取值范围是_____.
14.如图,四边形ABCD内接于⊙O,AD∥BC,BD平分∠ABC,∠A=126°,则∠BDC的度数为 _____.
三、(本大题共2小题,每小题6分,满分12分)
15.先化简,再求值:,其中.
16.如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,点A,B,C,D均在小正方形顶点上.
(1)在方格纸中画出面积为5的等腰直角△ABE,且点E在小正方形的顶点上;
(2)在方格纸中画出面积为3的等腰△CDF,其中CD为一腰,且点F在小正方形的顶点上;
(3)在(1)(2)条件下,连接EF,请直接写出线段EF长.
四、(本大题共2小题,每小题8分,满分16分)
17.已知y关于x的二次函数y=x -bx+b +b-5的图象与x轴有两个公共点.
(1)求b的取值范围;
(2)若b取满足条件的最大整数值,当m≤x≤时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
(3)若在自变量x的值满足b≤x≤b+3的情况下,对应函数y的最小值为,求此时二次函数的解析式.
18.如图,,与互余,,垂足为点,,请说明平分.
五、(本大题共2小题,每小题10分,满分20分)
19.如图1,在正方形ABCD中,点E在边BC上,点F在CD的延长线上,DF=BE.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,过点A作AH⊥EF垂足为H,交CD于点G,连接BH.
①求证:BEAB;
②图2中,若CE=4,DG=3,求BE的长.
20.如图,已知正比例函数和反比例函数的图像都经过点,且为双曲线上的一点,为坐标平面上一动点,垂直于轴,垂直于轴,垂足分别是、.
(1)写出正比例函数和反比例函数的关系式.
(2)当点在直线上运动时,直线上是否存在这样的点,使得与的面积相等?如果存在,请求出点的坐标;如果不存在,请说明理由.
七、(本大题共2小题,每小题12分,满分24分)
21.小亮推铅球时,铅球行进高度y(m)与水平距离x(m)之间的关系如图所示(二次函数图象的一部分).
(1)求y与x之间的函数关系式;
(2)求小亮推出铅球的水平距离.
22.如图,在△ABC中,∠ACB=90°,AC=BC,O点在△ABC内部,⊙O经过B、C两点且交AB于点D,连接CO并延长交线段AB于点G,以GD、GC为邻边作平行四边形GDEC.
(1)求证:直线DE是⊙O的切线;
(2)若DE=7,CE=5,求⊙O的半径.
八、(本大题共1小题,满分18分)
23.某数学兴趣小组在课外活动中,对多边形内两条互相垂直的线段做了如下探究:
(1)如图1,正方形中,,则 ;
(2)如图2,长方形中,,,则 ;
(3)如图3,长方形中,,,求的值,并说明理由.
(4)知识应用:如图4,中,,将沿翻着后得到,点在边上,点在边上,,求的值.
参考答案:
1.C2.D3.C4.D5.D6.A7.C8.C9.A10.C
11..
12.
13.
14.99°或99度
15. 解:
当时,原式=
16. 【详解】(1)如图所示:
根据勾股定理得:AB=AE=,BE=
∴,∴△ABE是等腰直角三角形,且面积=
(2)如图所示:
根据勾股定理得:DF =DC=, ∴△DCF是等腰三角形,且面积=
(3)根据勾股定理得:EF==.
17.(1);(2);(3)或
解:(1)由题意知,
即 ,
∴
解得: ;
(2)由题意,b=4,代入得:,
∴对称轴为直线.
又∵a=1>0,函数图象开口向上,
∴当时,y随x的增大而减小,
∴当x=时,,
当x=m时,y=,
解得:(不合题意,舍去);
∴.
(3) ,函数大致图象如图所示.
①当,即时,
函数y在顶点处取得最小值,有b-5=,
∴b=(不合题意,舍去)
②当,即时,
取值范围在对称轴左侧,y随x的增大而减小,
∴当x=b+3时,y最小值=,代入得
,
即,
解得:(不合题意,舍去),
∴此时二次函数的解析式为:
③当,即时,取值范围在对称轴右侧,y随x的增大而增大,
∴当x=b时,y最小值=,代入得
,
即,
解得:,
∴此时二次函数的解析式为:.
综上所述,符合题意的二次函数的解析式为:或
18. 解:∵∠1=∠E,∴AE∥BD,
∴∠B=∠2,
∵BD⊥AC,∴∠DFC=90°,
∴∠1+∠C=90°,
∵∠2+∠C=90°,∴∠1=∠2,
∴∠B=∠1.
在△DFC与△BFA中,
,
∴△DFC≌△BFA(AAS),
∴DF=BF,
∴AC平分DB.
19. 解:(1)由正方形ABCD,得 AB=AD,∠B=∠ADF=∠BAD=90°,
在△ABE和△ADF中,
∴∠BAE=∠FAD,AE=AF.
∴∠BAD=∠BAE+∠EAD=∠FAD+∠EAD=90°.
即得∠EAF=90°,
又∵AE=AF,
∴△AEF是等腰直角三角形;
(2)①连接AC,
在正方形ABCD中,∠CAB=45°,,AB=CD,
∵AE=AF,∠EAF=90°,且AH⊥EF
∴∠EAH=45°,,
∴,
∵∠BAH=∠BAE+∠EAH=∠BAE+45°,∠CAF=∠DAF+∠DAC=∠DAF+45°,
∴∠BAH=∠CAF,
∴△ACF∽△ABH,
∴,
∴,
∵CF=CD+DF=AB+BE,
∴BEAB;
②连接BG,设BE=x,则DF=x,
∵CE=4,DG=3,
∴CB=x+4,FG=x+3,CG=x+4-3=x+1,
∵△AEF是等腰直角三角形,AH⊥EF
∴AH垂直平分EF,
∴FG=EG=x+3,
在Rt△ECG中,EG2=CG2+EC2,
∴(x+3)2=(x+1)2+16,
∴x=2,
∴BE=2
20.(1)正比例函数的解析式为,反比例函数的解析式为;
(2)在直线上存在这样的点或,使得与面积相等.
【详解】(1)设反比例函数的解析式为,正比例函数的解析式为.
∵正比例函数和反比例函数的图像都经过点,∴,. ∴,.
∴正比例函数的解析式为,反比例函数的解析式为.
(2)当点在直线上运动时,假设在直线上存在这一的点,使得与面积相等,则.
∵,∴,解得.
当时,. 当时,.
故在直线上存在这样的点或,使得与面积相等.
21.(1);(2)小亮推出铅球的水平距离是10m.
解:(1)设y与x之间的函数关系式为:,
∵点在的图象上,
∴
解得,,
∴y与x之间的函数关系式是:;
(2)将代入,得,
解得,
由图可知,小亮推出的距离为正值,,不符合题意,舍去,
故小亮推出铅球的水平距离是10m,
答:小亮推出铅球的水平距离是10m.
22. (1)证明:连接OD,
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∴∠COD=2∠ABC=90°,
∵四边形GDEC是平行四边形,
∴DE∥CG,
∴∠ODE+∠COD=180°,
∴∠ODE=90°,即OD⊥DE,
∵OD是半径,
∴直线DE是⊙O的切线;
(2)解:设⊙O的半径为r,
∵四边形GDEC是平行四边形,
∴CG=DE=7,DG=CE=5,
∵∠GOD=90°,
∴OD2+OG2=DG2,即r2+(7﹣r)2=52,
解得:r1=3,r2=4,
当r=3时,OG=4>3,此时点G在⊙O外,不合题意,舍去,
∴r=4,即⊙O的半径4.
23.(1)1
(2)
(3),理由见解析
(4)的值为
【解析】
(1)如图1,∵四边形ABCD是正方形,
∴AD=DC,∠EAD=∠FDC=90°,
∵,
∴∠ADE+∠DFC=90°,∠DCF+∠DFC=90°,
∴∠ADE=∠DCF,
∴△ADE≌△DCF,
∴DE=CF,
∴1,
故答案为:1.
(2)如图2,∵四边形ABCD是矩形,
∴∠BAD=∠ADC=90°,
∵,
∴∠ADB+∠DEC=90°,∠DCE+∠DEC=90°,
∴∠ADB=∠DCE,
∴△ADB∽△DCE,
∴,
∵,
∴,
故答案为:.
(3)如图3,过点F作FH⊥BC,垂足为H,
∵四边形ABCD是矩形,
∴AD∥BC,∠DAE=90°,
∴FH⊥AD,
∴∠HFG+∠DFG=90°,
∵,
∴∠FDE+∠DFG=90°,
∴∠HFG =∠FDE,
∴△ADE∽△HFG,
∴,
∵四边形ABCD是矩形,
∴∠DAE=90°,∠ABG=90°,AB=CD,
∴FH⊥AD,
∴四边形ABHF是矩形,
∴AB=CD=FH,
∵,
∴=,
故答案为:.
(4)如图4,延长AB,过点C作,
过点D作,
由上可知,
,
,
由折叠知 ,
,
∵,,∠A=90°,
∴∠BCD=90°,
∴∠DCG+∠BCH=90°,∠HBC+∠BCH=90°,
∴∠HBC=∠GCD,
∴,
,
设
,
解得,
.
答案第1页,共2页
2 / 2
2021-2022学年度第二学期开学考试
九年级数学试题
第I卷(选择题)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列各选项的图形中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
2.如图,已知,若,,,则的长为( )
A.1.5 B.2 C.2.5 D.3
3.将抛物线y=x2先向右平移2个单位长度,再向上平移4个单位长度,得到的新的抛物线的解析式为( )
A.y=(x+2)2+4 B.y=(x+2)2﹣4
C.y=(x﹣2)2+4 D.y=(x﹣2)2﹣4
4.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于点E,AE平分∠BAC,AO=CO,AD=DC=2,下面结论:①AC=2AB;②AB=;③S△ADC=2S△ABE;④BO⊥AE,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.在同一平面直角坐标系中,函数与的图象可能是( )
A. B.
C. D.
6.在矩形ABCD中,AB=2,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
7.若点在反比例函数的图象上,则抛物线与轴的交点个数是( )
A.2 B.1 C.0 D.无法确定
8.如图,与都是等腰三角形,且,,若,则与的面积比为( )
A. B. C. D.
9.已知,将如图的三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB.则∠α的余弦值为( )
A. B. C. D.1
10.如图,二次函数的图象经过点,其对称轴为直线,有下列结论:①;②;③;④;⑤若,是抛物线上两点,且,则实数的取值范围是.其中正确结论是( )
A.①③④ B.②④⑤ C.①③⑤ D.①③④⑤
第II卷 非选择题
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知,则的值为_____.
12.如图,菱形的周长为24,对角线与交于点O,,则_________.
13.已知反比例函数(k为常数)在每一象限内,y随x的增大而增大,则k的取值范围是_____.
14.如图,四边形ABCD内接于⊙O,AD∥BC,BD平分∠ABC,∠A=126°,则∠BDC的度数为 _____.
三、(本大题共2小题,每小题6分,满分12分)
15.先化简,再求值:,其中.
16.如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,点A,B,C,D均在小正方形顶点上.
(1)在方格纸中画出面积为5的等腰直角△ABE,且点E在小正方形的顶点上;
(2)在方格纸中画出面积为3的等腰△CDF,其中CD为一腰,且点F在小正方形的顶点上;
(3)在(1)(2)条件下,连接EF,请直接写出线段EF长.
四、(本大题共2小题,每小题8分,满分16分)
17.已知y关于x的二次函数y=x -bx+b +b-5的图象与x轴有两个公共点.
(1)求b的取值范围;
(2)若b取满足条件的最大整数值,当m≤x≤时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
(3)若在自变量x的值满足b≤x≤b+3的情况下,对应函数y的最小值为,求此时二次函数的解析式.
18.如图,,与互余,,垂足为点,,请说明平分.
五、(本大题共2小题,每小题10分,满分20分)
19.如图1,在正方形ABCD中,点E在边BC上,点F在CD的延长线上,DF=BE.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,过点A作AH⊥EF垂足为H,交CD于点G,连接BH.
①求证:BEAB;
②图2中,若CE=4,DG=3,求BE的长.
20.如图,已知正比例函数和反比例函数的图像都经过点,且为双曲线上的一点,为坐标平面上一动点,垂直于轴,垂直于轴,垂足分别是、.
(1)写出正比例函数和反比例函数的关系式.
(2)当点在直线上运动时,直线上是否存在这样的点,使得与的面积相等?如果存在,请求出点的坐标;如果不存在,请说明理由.
七、(本大题共2小题,每小题12分,满分24分)
21.小亮推铅球时,铅球行进高度y(m)与水平距离x(m)之间的关系如图所示(二次函数图象的一部分).
(1)求y与x之间的函数关系式;
(2)求小亮推出铅球的水平距离.
22.如图,在△ABC中,∠ACB=90°,AC=BC,O点在△ABC内部,⊙O经过B、C两点且交AB于点D,连接CO并延长交线段AB于点G,以GD、GC为邻边作平行四边形GDEC.
(1)求证:直线DE是⊙O的切线;
(2)若DE=7,CE=5,求⊙O的半径.
八、(本大题共1小题,满分18分)
23.某数学兴趣小组在课外活动中,对多边形内两条互相垂直的线段做了如下探究:
(1)如图1,正方形中,,则 ;
(2)如图2,长方形中,,,则 ;
(3)如图3,长方形中,,,求的值,并说明理由.
(4)知识应用:如图4,中,,将沿翻着后得到,点在边上,点在边上,,求的值.
参考答案:
1.C2.D3.C4.D5.D6.A7.C8.C9.A10.C
11..
12.
13.
14.99°或99度
15. 解:
当时,原式=
16. 【详解】(1)如图所示:
根据勾股定理得:AB=AE=,BE=
∴,∴△ABE是等腰直角三角形,且面积=
(2)如图所示:
根据勾股定理得:DF =DC=, ∴△DCF是等腰三角形,且面积=
(3)根据勾股定理得:EF==.
17.(1);(2);(3)或
解:(1)由题意知,
即 ,
∴
解得: ;
(2)由题意,b=4,代入得:,
∴对称轴为直线.
又∵a=1>0,函数图象开口向上,
∴当时,y随x的增大而减小,
∴当x=时,,
当x=m时,y=,
解得:(不合题意,舍去);
∴.
(3) ,函数大致图象如图所示.
①当,即时,
函数y在顶点处取得最小值,有b-5=,
∴b=(不合题意,舍去)
②当,即时,
取值范围在对称轴左侧,y随x的增大而减小,
∴当x=b+3时,y最小值=,代入得
,
即,
解得:(不合题意,舍去),
∴此时二次函数的解析式为:
③当,即时,取值范围在对称轴右侧,y随x的增大而增大,
∴当x=b时,y最小值=,代入得
,
即,
解得:,
∴此时二次函数的解析式为:.
综上所述,符合题意的二次函数的解析式为:或
18. 解:∵∠1=∠E,∴AE∥BD,
∴∠B=∠2,
∵BD⊥AC,∴∠DFC=90°,
∴∠1+∠C=90°,
∵∠2+∠C=90°,∴∠1=∠2,
∴∠B=∠1.
在△DFC与△BFA中,
,
∴△DFC≌△BFA(AAS),
∴DF=BF,
∴AC平分DB.
19. 解:(1)由正方形ABCD,得 AB=AD,∠B=∠ADF=∠BAD=90°,
在△ABE和△ADF中,
∴∠BAE=∠FAD,AE=AF.
∴∠BAD=∠BAE+∠EAD=∠FAD+∠EAD=90°.
即得∠EAF=90°,
又∵AE=AF,
∴△AEF是等腰直角三角形;
(2)①连接AC,
在正方形ABCD中,∠CAB=45°,,AB=CD,
∵AE=AF,∠EAF=90°,且AH⊥EF
∴∠EAH=45°,,
∴,
∵∠BAH=∠BAE+∠EAH=∠BAE+45°,∠CAF=∠DAF+∠DAC=∠DAF+45°,
∴∠BAH=∠CAF,
∴△ACF∽△ABH,
∴,
∴,
∵CF=CD+DF=AB+BE,
∴BEAB;
②连接BG,设BE=x,则DF=x,
∵CE=4,DG=3,
∴CB=x+4,FG=x+3,CG=x+4-3=x+1,
∵△AEF是等腰直角三角形,AH⊥EF
∴AH垂直平分EF,
∴FG=EG=x+3,
在Rt△ECG中,EG2=CG2+EC2,
∴(x+3)2=(x+1)2+16,
∴x=2,
∴BE=2
20.(1)正比例函数的解析式为,反比例函数的解析式为;
(2)在直线上存在这样的点或,使得与面积相等.
【详解】(1)设反比例函数的解析式为,正比例函数的解析式为.
∵正比例函数和反比例函数的图像都经过点,∴,. ∴,.
∴正比例函数的解析式为,反比例函数的解析式为.
(2)当点在直线上运动时,假设在直线上存在这一的点,使得与面积相等,则.
∵,∴,解得.
当时,. 当时,.
故在直线上存在这样的点或,使得与面积相等.
21.(1);(2)小亮推出铅球的水平距离是10m.
解:(1)设y与x之间的函数关系式为:,
∵点在的图象上,
∴
解得,,
∴y与x之间的函数关系式是:;
(2)将代入,得,
解得,
由图可知,小亮推出的距离为正值,,不符合题意,舍去,
故小亮推出铅球的水平距离是10m,
答:小亮推出铅球的水平距离是10m.
22. (1)证明:连接OD,
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∴∠COD=2∠ABC=90°,
∵四边形GDEC是平行四边形,
∴DE∥CG,
∴∠ODE+∠COD=180°,
∴∠ODE=90°,即OD⊥DE,
∵OD是半径,
∴直线DE是⊙O的切线;
(2)解:设⊙O的半径为r,
∵四边形GDEC是平行四边形,
∴CG=DE=7,DG=CE=5,
∵∠GOD=90°,
∴OD2+OG2=DG2,即r2+(7﹣r)2=52,
解得:r1=3,r2=4,
当r=3时,OG=4>3,此时点G在⊙O外,不合题意,舍去,
∴r=4,即⊙O的半径4.
23.(1)1
(2)
(3),理由见解析
(4)的值为
【解析】
(1)如图1,∵四边形ABCD是正方形,
∴AD=DC,∠EAD=∠FDC=90°,
∵,
∴∠ADE+∠DFC=90°,∠DCF+∠DFC=90°,
∴∠ADE=∠DCF,
∴△ADE≌△DCF,
∴DE=CF,
∴1,
故答案为:1.
(2)如图2,∵四边形ABCD是矩形,
∴∠BAD=∠ADC=90°,
∵,
∴∠ADB+∠DEC=90°,∠DCE+∠DEC=90°,
∴∠ADB=∠DCE,
∴△ADB∽△DCE,
∴,
∵,
∴,
故答案为:.
(3)如图3,过点F作FH⊥BC,垂足为H,
∵四边形ABCD是矩形,
∴AD∥BC,∠DAE=90°,
∴FH⊥AD,
∴∠HFG+∠DFG=90°,
∵,
∴∠FDE+∠DFG=90°,
∴∠HFG =∠FDE,
∴△ADE∽△HFG,
∴,
∵四边形ABCD是矩形,
∴∠DAE=90°,∠ABG=90°,AB=CD,
∴FH⊥AD,
∴四边形ABHF是矩形,
∴AB=CD=FH,
∵,
∴=,
故答案为:.
(4)如图4,延长AB,过点C作,
过点D作,
由上可知,
,
,
由折叠知 ,
,
∵,,∠A=90°,
∴∠BCD=90°,
∴∠DCG+∠BCH=90°,∠HBC+∠BCH=90°,
∴∠HBC=∠GCD,
∴,
,
设
,
解得,
.
答案第1页,共2页
2 / 2
同课章节目录
