安徽省滁州市定远县育才学校2021-2022学年七年级下学期开学考数学试题(word版含答案)
文档属性
| 名称 | 安徽省滁州市定远县育才学校2021-2022学年七年级下学期开学考数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 573.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 21:51:55 | ||
图片预览



文档简介
定远育才学校2021-2022学年度第二学期开学考试
七年级数学试题
第I卷(选择题)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.某县为了传承中华优秀传统文化,组织了一次全县600名学生参加的“中华经典诵读”大赛.为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析.在这个问题中,下列说法中正确的是( )
A.这600名学生的“中华经典诵读”大赛成绩的全体是总体
B.50名学生是总体的一个样本
C.每个学生是个体
D.样本容量是50名
2.在中国共产党第十八次全国代表大会期间,新民网发起了有关发生的调查,截止到2012年11月15日13时30分,共吸引了约262900人参与,数据显示社会民生问题位列网友最关心的问题首位,请将262900用科学计数法表示为( )
A. B. C. D.
3.已知,两数在数轴上的位置如图所示,则化简代数式的结果是( )
A.1 B. C. D.-1
4.计算|﹣2|+2﹣1的结果是( )
A.﹣1 B.0 C.1 D.2
5.下列各式中,是同类项的是( )
A.与 B.与 C.与 D.与
6.永州市在五一期间举办了“阳明山杜鹃花旅游文化节”,吸引了众多游客前去观光赏花.在文化节开幕式当天,从早晨8:00开始每小时进入阳明山景区的游客人数约为1 000人,同时每小时走出景区的游客人数约为600人.已知阳明山景区游客的饱和人数为2 000人,则据此可知开幕式当天该景区游客人数饱和的时间约为( )
A.10:00 B.12:00 C.13:00 D.16:00
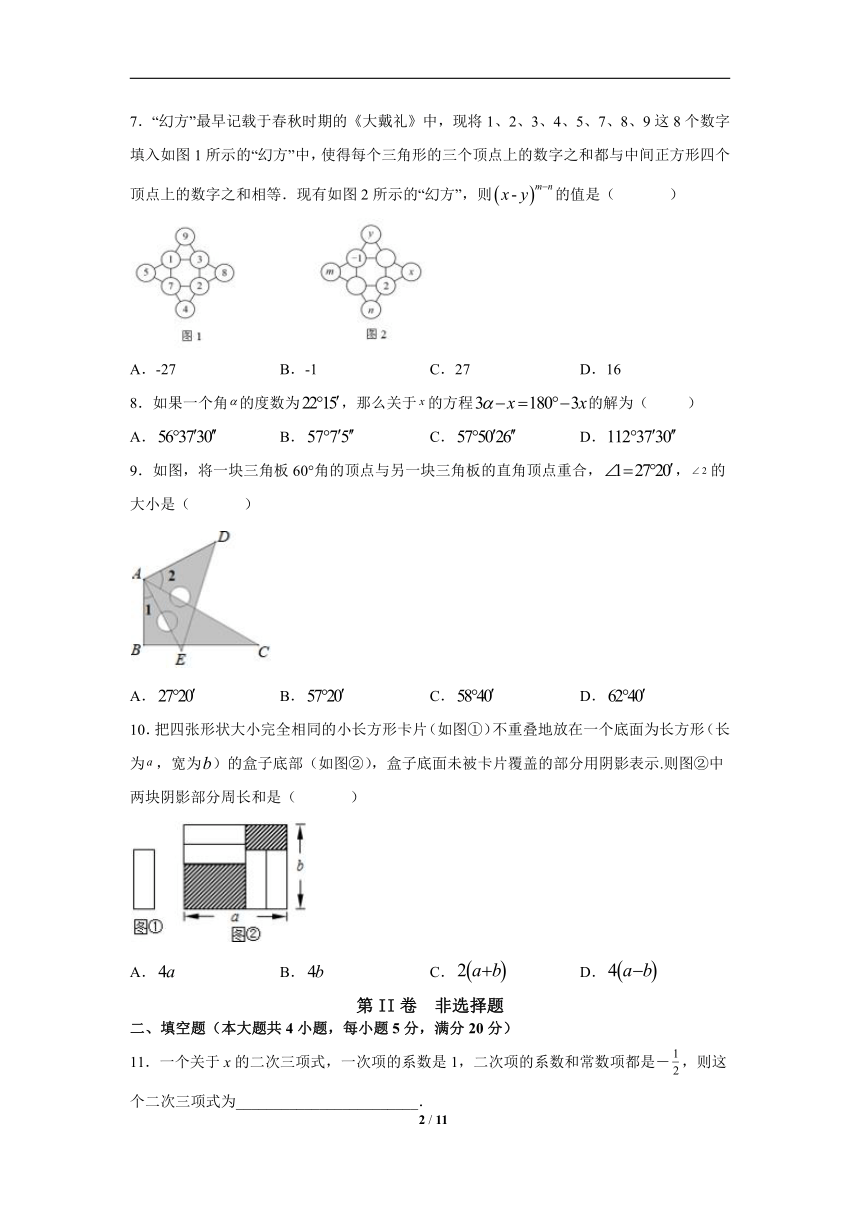
7.“幻方”最早记载于春秋时期的《大戴礼》中,现将1、2、3、4、5、7、8、9这8个数字填入如图1所示的“幻方”中,使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.现有如图2所示的“幻方”,则的值是( )
A.-27 B.-1 C.27 D.16
8.如果一个角的度数为,那么关于的方程的解为( )
A. B. C. D.
9.如图,将一块三角板60°角的顶点与另一块三角板的直角顶点重合,,的大小是( )
A. B. C. D.
10.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为,宽为)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分周长和是( )
A. B. C. D.
第II卷 非选择题
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个关于x的二次三项式,一次项的系数是1,二次项的系数和常数项都是-,则这个二次三项式为________________________.
12.已知是方程的解,则=________.
13.下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第___个图形中面积为1的正方形有2024个.
14.已知点O是数轴的原点,点A、B、C在数轴上对应的数分别是﹣12、b、c,且b、c满足(b﹣9)2+|c﹣15|=0,动点P从点A出发以2单位/秒的速度向右运动,同时点Q从点C出发,以1个单位/秒速度向左运动,O、B两点之间为“变速区”,规则为从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速,从点B运动到点O期间速度变为原来的3倍,之后立刻恢复原速,运动时间为 _____秒时,P、Q两点到点B的距离相等.
三、(本大题共2小题,每小题5分,满分10分)
15.解方程:
(1);
(2)解方程:.
四、(本大题共2小题,每小题5分,满分10分)
16.计算题
(1)
(2)
五、(本大题共2小题,每小题6分,满分12分)
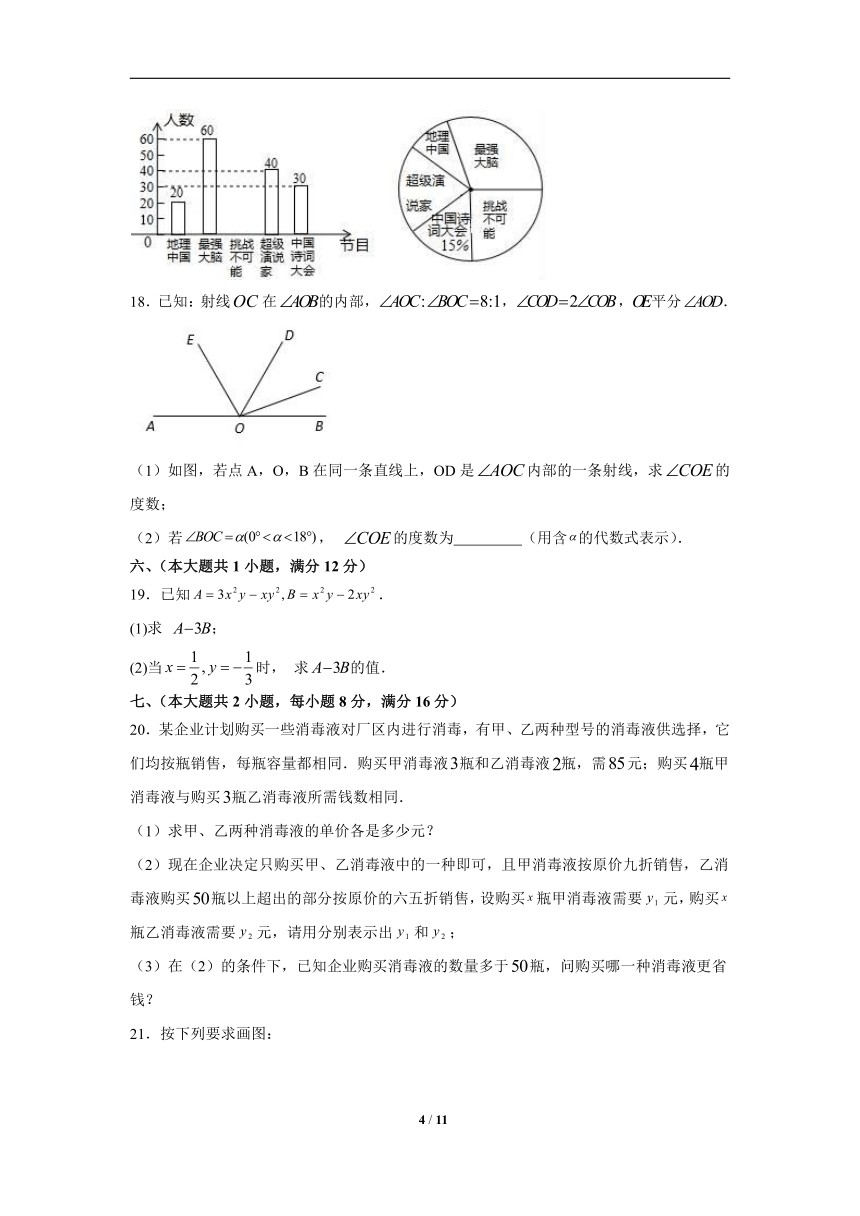
17.我市某中学为了了解孩子们对《中国诗词大会》,《挑战不可能》,《最强大脑》,《超级演说家》,《地理中国》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:
(1)本次调查中共抽取了 名学生.
(2)补全条形统计图.
(3)在扇形统计图中,喜爱《地理中国》节目的人数所在的扇形的圆心角是 度.
(4)若该学校有2000人,请你估计该学校喜欢《最强大脑》节目的学生人数是多少人?
18.已知:射线在的内部,,,平分.
(1)如图,若点A,O,B在同一条直线上,OD是内部的一条射线,求的度数;
(2)若, 的度数为 (用含的代数式表示).
六、(本大题共1小题,满分12分)
19.已知.
(1)求 ;
(2)当时, 求的值.
七、(本大题共2小题,每小题8分,满分16分)
20.某企业计划购买一些消毒液对厂区内进行消毒,有甲、乙两种型号的消毒液供选择,它们均按瓶销售,每瓶容量都相同.购买甲消毒液瓶和乙消毒液瓶,需元;购买瓶甲消毒液与购买瓶乙消毒液所需钱数相同.
(1)求甲、乙两种消毒液的单价各是多少元?
(2)现在企业决定只购买甲、乙消毒液中的一种即可,且甲消毒液按原价九折销售,乙消毒液购买瓶以上超出的部分按原价的六五折销售,设购买瓶甲消毒液需要元,购买瓶乙消毒液需要元,请用分别表示出和;
(3)在(2)的条件下,已知企业购买消毒液的数量多于瓶,问购买哪一种消毒液更省钱?
21.按下列要求画图:
(1)如图1,已知三点A,B,C,画直线AB,射线AC;
(2)如图2.已知线段a,b,作一条线段MN,使(尺规作图,保留作图痕迹).
八、(本大题共1小题,满分14分)
22.观察下列等式:
①;②;③…
根据上述等式的规律,解答下列问题:
(1)请写出第④个等式:_____________;
(2)写出第n个等式(用含有n的等式表示):_____________;
(3)应用你发现的规律,计算:.
九、(本大题共1小题,满分16分)
23.已知O是直线MN上一点,∠MOA=40°,∠AOB=90°,∠COD与∠AOB都在直线MN的上方,且射线OC在射线OD的左侧.
(1)如图1,射线OC在∠AOB的内部,如果∠COD=90°,那么图中与∠AOC相等的角是 ,其依据是: .
(2)如图2,用直尺和圆规作∠AOB的平分线OP,如果∠COD=60°,且OC平分∠AOP,那么∠DON= °;(保留作图痕迹,不要求写出作法和结论)
(3)如果∠COD=60°,设∠AOC=m°(0<m<80,且m≠30),用含m的式子表示∠BOD的度数.(直接写出结论)
参考答案:
1.A2.C3.B4.D5.B6.C7.A8.A9.B10.B
11.
12.6
13.404
14.或30
15.(1);(2)
解:(1)
移项、合并得,,
系数化为1,;
(2)
去分母得:
去括号得:
移项、合并得:
16.(1);(2)
解:(1)原式;
(2)原式.
17.(1)200;(2)补图见解析;(3)36;(4)600人.
解:(1)30÷15%=200名,
答:本次调查中共抽取了200名学生;
故答案为200;
(2)喜爱《挑战不可能》节目的人数=200﹣20﹣60﹣40﹣30=50名,
补全条形统计图如图所示;
(3)喜爱《地理中国》节目的人数所在的扇形的圆心角是360°×=36度;
故答案为36;
(4)2000×=600名,
答:该学校喜欢《最强大脑》节目的学生人数是600人.
18.(1);(2)或.
【详解】(1)∵,点A、O、B再同一条直线上.
∴,.
由题意,
∴.
∵平分,
∴,
∴.
(2)①当射线OD在内部时,如图.
∵,,,
∴,,.
∴,
∵平分,
∴.
∴.
②当射线OD在外部时,如图.
同理可知:,,.
∴,
∴,
∵平分,
∴.
∴.
故答案为:或.
19.(1);
(2)
【解析】
(1)∵
∴
(2)当时
20.(1)甲:15元,乙:20元;(2) ;(3)见解析
解:(1)设甲消毒液的单价为a元,乙消毒液的单价为b元,则
解得
答:甲消毒液的单价为15元,乙消毒液的单价为20元.
(2)根据题意,得y1=15×0.9x=13.5x;
当0≤x≤50时,y2=20x;
当x>50时,y2=50×20+20×0.65×(x-50)=13x+350.
(3)由于x>50,所以分三种情况:
当y1<y2时,得13.5x<13x+350,解得x<700,此时选择甲;
当y1=y2时,得13.5x=13x+350,解得x=700,此时选择甲、乙花费相同;
当y1>y2时,得13.5x>13x+350,解得x>700,此时选择乙.
综上所述:当50<x<700时,选择购买甲消毒液更省钱;当x=700时,选择购买甲、乙两种消毒液花费相同;当x>700时,选择购买乙消毒液更省钱.
21.(1)解:如图,直线 射线是所求作的直线与射线,
(2)解:如图,线段即为所求作的线段,
22.(1)
(2)
(3)
(1)解:∵①;②;③,…,
∴,
故答案是:;
(2)解:由(1)可知,第n个等式为:,
故答案是:;
(3)解:
.
23.
(1)解:如图1中,
,
,
(等角的余角相等),
故答案为:等角的余角相等.
(2)解:如图2中,如图,射线即为所求.
,,
,
平分,
,
平分,
,
,
.
(3)解:如图中,当时,
.
如图中,当时,
.
综上所述,满足条件的的值为或.
答案第1页,共2页
2 / 2
七年级数学试题
第I卷(选择题)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.某县为了传承中华优秀传统文化,组织了一次全县600名学生参加的“中华经典诵读”大赛.为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析.在这个问题中,下列说法中正确的是( )
A.这600名学生的“中华经典诵读”大赛成绩的全体是总体
B.50名学生是总体的一个样本
C.每个学生是个体
D.样本容量是50名
2.在中国共产党第十八次全国代表大会期间,新民网发起了有关发生的调查,截止到2012年11月15日13时30分,共吸引了约262900人参与,数据显示社会民生问题位列网友最关心的问题首位,请将262900用科学计数法表示为( )
A. B. C. D.
3.已知,两数在数轴上的位置如图所示,则化简代数式的结果是( )
A.1 B. C. D.-1
4.计算|﹣2|+2﹣1的结果是( )
A.﹣1 B.0 C.1 D.2
5.下列各式中,是同类项的是( )
A.与 B.与 C.与 D.与
6.永州市在五一期间举办了“阳明山杜鹃花旅游文化节”,吸引了众多游客前去观光赏花.在文化节开幕式当天,从早晨8:00开始每小时进入阳明山景区的游客人数约为1 000人,同时每小时走出景区的游客人数约为600人.已知阳明山景区游客的饱和人数为2 000人,则据此可知开幕式当天该景区游客人数饱和的时间约为( )
A.10:00 B.12:00 C.13:00 D.16:00
7.“幻方”最早记载于春秋时期的《大戴礼》中,现将1、2、3、4、5、7、8、9这8个数字填入如图1所示的“幻方”中,使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.现有如图2所示的“幻方”,则的值是( )
A.-27 B.-1 C.27 D.16
8.如果一个角的度数为,那么关于的方程的解为( )
A. B. C. D.
9.如图,将一块三角板60°角的顶点与另一块三角板的直角顶点重合,,的大小是( )
A. B. C. D.
10.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为,宽为)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分周长和是( )
A. B. C. D.
第II卷 非选择题
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个关于x的二次三项式,一次项的系数是1,二次项的系数和常数项都是-,则这个二次三项式为________________________.
12.已知是方程的解,则=________.
13.下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第___个图形中面积为1的正方形有2024个.
14.已知点O是数轴的原点,点A、B、C在数轴上对应的数分别是﹣12、b、c,且b、c满足(b﹣9)2+|c﹣15|=0,动点P从点A出发以2单位/秒的速度向右运动,同时点Q从点C出发,以1个单位/秒速度向左运动,O、B两点之间为“变速区”,规则为从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速,从点B运动到点O期间速度变为原来的3倍,之后立刻恢复原速,运动时间为 _____秒时,P、Q两点到点B的距离相等.
三、(本大题共2小题,每小题5分,满分10分)
15.解方程:
(1);
(2)解方程:.
四、(本大题共2小题,每小题5分,满分10分)
16.计算题
(1)
(2)
五、(本大题共2小题,每小题6分,满分12分)
17.我市某中学为了了解孩子们对《中国诗词大会》,《挑战不可能》,《最强大脑》,《超级演说家》,《地理中国》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:
(1)本次调查中共抽取了 名学生.
(2)补全条形统计图.
(3)在扇形统计图中,喜爱《地理中国》节目的人数所在的扇形的圆心角是 度.
(4)若该学校有2000人,请你估计该学校喜欢《最强大脑》节目的学生人数是多少人?
18.已知:射线在的内部,,,平分.
(1)如图,若点A,O,B在同一条直线上,OD是内部的一条射线,求的度数;
(2)若, 的度数为 (用含的代数式表示).
六、(本大题共1小题,满分12分)
19.已知.
(1)求 ;
(2)当时, 求的值.
七、(本大题共2小题,每小题8分,满分16分)
20.某企业计划购买一些消毒液对厂区内进行消毒,有甲、乙两种型号的消毒液供选择,它们均按瓶销售,每瓶容量都相同.购买甲消毒液瓶和乙消毒液瓶,需元;购买瓶甲消毒液与购买瓶乙消毒液所需钱数相同.
(1)求甲、乙两种消毒液的单价各是多少元?
(2)现在企业决定只购买甲、乙消毒液中的一种即可,且甲消毒液按原价九折销售,乙消毒液购买瓶以上超出的部分按原价的六五折销售,设购买瓶甲消毒液需要元,购买瓶乙消毒液需要元,请用分别表示出和;
(3)在(2)的条件下,已知企业购买消毒液的数量多于瓶,问购买哪一种消毒液更省钱?
21.按下列要求画图:
(1)如图1,已知三点A,B,C,画直线AB,射线AC;
(2)如图2.已知线段a,b,作一条线段MN,使(尺规作图,保留作图痕迹).
八、(本大题共1小题,满分14分)
22.观察下列等式:
①;②;③…
根据上述等式的规律,解答下列问题:
(1)请写出第④个等式:_____________;
(2)写出第n个等式(用含有n的等式表示):_____________;
(3)应用你发现的规律,计算:.
九、(本大题共1小题,满分16分)
23.已知O是直线MN上一点,∠MOA=40°,∠AOB=90°,∠COD与∠AOB都在直线MN的上方,且射线OC在射线OD的左侧.
(1)如图1,射线OC在∠AOB的内部,如果∠COD=90°,那么图中与∠AOC相等的角是 ,其依据是: .
(2)如图2,用直尺和圆规作∠AOB的平分线OP,如果∠COD=60°,且OC平分∠AOP,那么∠DON= °;(保留作图痕迹,不要求写出作法和结论)
(3)如果∠COD=60°,设∠AOC=m°(0<m<80,且m≠30),用含m的式子表示∠BOD的度数.(直接写出结论)
参考答案:
1.A2.C3.B4.D5.B6.C7.A8.A9.B10.B
11.
12.6
13.404
14.或30
15.(1);(2)
解:(1)
移项、合并得,,
系数化为1,;
(2)
去分母得:
去括号得:
移项、合并得:
16.(1);(2)
解:(1)原式;
(2)原式.
17.(1)200;(2)补图见解析;(3)36;(4)600人.
解:(1)30÷15%=200名,
答:本次调查中共抽取了200名学生;
故答案为200;
(2)喜爱《挑战不可能》节目的人数=200﹣20﹣60﹣40﹣30=50名,
补全条形统计图如图所示;
(3)喜爱《地理中国》节目的人数所在的扇形的圆心角是360°×=36度;
故答案为36;
(4)2000×=600名,
答:该学校喜欢《最强大脑》节目的学生人数是600人.
18.(1);(2)或.
【详解】(1)∵,点A、O、B再同一条直线上.
∴,.
由题意,
∴.
∵平分,
∴,
∴.
(2)①当射线OD在内部时,如图.
∵,,,
∴,,.
∴,
∵平分,
∴.
∴.
②当射线OD在外部时,如图.
同理可知:,,.
∴,
∴,
∵平分,
∴.
∴.
故答案为:或.
19.(1);
(2)
【解析】
(1)∵
∴
(2)当时
20.(1)甲:15元,乙:20元;(2) ;(3)见解析
解:(1)设甲消毒液的单价为a元,乙消毒液的单价为b元,则
解得
答:甲消毒液的单价为15元,乙消毒液的单价为20元.
(2)根据题意,得y1=15×0.9x=13.5x;
当0≤x≤50时,y2=20x;
当x>50时,y2=50×20+20×0.65×(x-50)=13x+350.
(3)由于x>50,所以分三种情况:
当y1<y2时,得13.5x<13x+350,解得x<700,此时选择甲;
当y1=y2时,得13.5x=13x+350,解得x=700,此时选择甲、乙花费相同;
当y1>y2时,得13.5x>13x+350,解得x>700,此时选择乙.
综上所述:当50<x<700时,选择购买甲消毒液更省钱;当x=700时,选择购买甲、乙两种消毒液花费相同;当x>700时,选择购买乙消毒液更省钱.
21.(1)解:如图,直线 射线是所求作的直线与射线,
(2)解:如图,线段即为所求作的线段,
22.(1)
(2)
(3)
(1)解:∵①;②;③,…,
∴,
故答案是:;
(2)解:由(1)可知,第n个等式为:,
故答案是:;
(3)解:
.
23.
(1)解:如图1中,
,
,
(等角的余角相等),
故答案为:等角的余角相等.
(2)解:如图2中,如图,射线即为所求.
,,
,
平分,
,
平分,
,
,
.
(3)解:如图中,当时,
.
如图中,当时,
.
综上所述,满足条件的的值为或.
答案第1页,共2页
2 / 2
同课章节目录
