2021-2022学年高一下学期数学人教A版(2019)必修第二册6.4.3正弦定理、余弦定理的应用举例课件(19张ppt)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册6.4.3正弦定理、余弦定理的应用举例课件(19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
6.4.3 余弦定理、正弦定理
正弦定理、余弦定理的应用举例
1.进一步熟悉余弦定理、正弦定理;
2.了解常用的测量相关术语;
3.能运用余弦定理、正弦定理等知识和方法解决
有关距离、高度、角度的实际问题。
一、学习目标(1分钟)
阅读教材P42--43,思考下列问题:
1、课本介绍了正弦定理和余弦定理在实际测量中有几种应用?
(1). 测量距离.
(2). 测量高度.
(3). 测量角度.
二、问题导学(3分钟)
2、什么叫基线
1、基线的定义
2、选择基线的原则
在测量过程中,为使测量工具有较高的精确度,应根据实际需要选取合适的基线长度,一般来说,基线_______,测量的精确度越高.
越长
在测量过程中,我们把根据测量的需要而确定的线段叫做基线.
三、点拨精讲(25分钟)
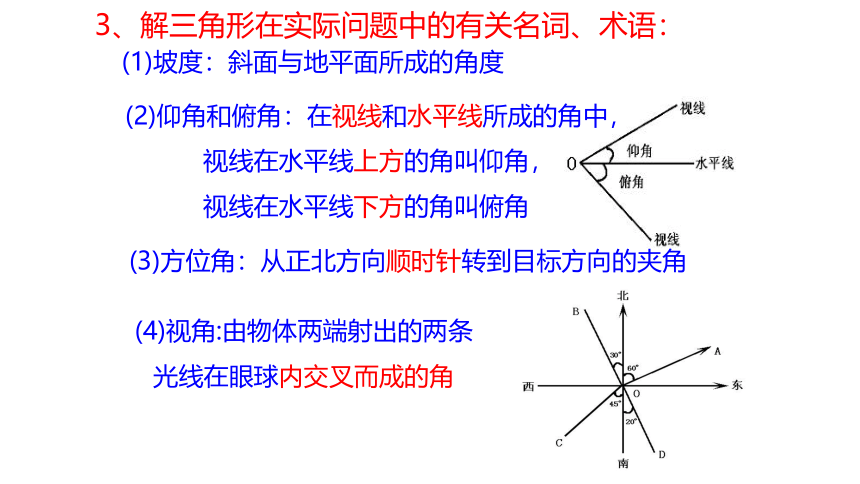
3、解三角形在实际问题中的有关名词、术语:
(2)仰角和俯角:在视线和水平线所成的角中,
视线在水平线上方的角叫仰角,
视线在水平线下方的角叫俯角
(3)方位角:从正北方向顺时针转到目标方向的夹角
(4)视角:由物体两端射出的两条
光线在眼球内交叉而成的角
(1)坡度:斜面与地平面所成的角度
题型一 不能到达两点间的距离问题
例1 如图, A,B两点都在河的对岸(不可到达),设计一种测量A,B 两点间的距离的方法.并求出A,B 间的距离。
跟踪训练1
题型二 测量高度问题
例2 如图,AB是底部B不可到达的一座建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法.并求出建筑物的高度。
跟踪训练2
题型三 测量角度问题
例3
跟踪训练3
实际问题
抽象概括
示意图
数学模型
推理
演算
数学模型的解
实际问题的解
还原说明
1.测量距离问题、高度问题、角度问题、面积问题、航海问题等实际应用解题思路:
四、课堂小结(2分钟)
五、当堂检测(14分钟)
6.4.3 余弦定理、正弦定理
正弦定理、余弦定理的应用举例
1.进一步熟悉余弦定理、正弦定理;
2.了解常用的测量相关术语;
3.能运用余弦定理、正弦定理等知识和方法解决
有关距离、高度、角度的实际问题。
一、学习目标(1分钟)
阅读教材P42--43,思考下列问题:
1、课本介绍了正弦定理和余弦定理在实际测量中有几种应用?
(1). 测量距离.
(2). 测量高度.
(3). 测量角度.
二、问题导学(3分钟)
2、什么叫基线
1、基线的定义
2、选择基线的原则
在测量过程中,为使测量工具有较高的精确度,应根据实际需要选取合适的基线长度,一般来说,基线_______,测量的精确度越高.
越长
在测量过程中,我们把根据测量的需要而确定的线段叫做基线.
三、点拨精讲(25分钟)
3、解三角形在实际问题中的有关名词、术语:
(2)仰角和俯角:在视线和水平线所成的角中,
视线在水平线上方的角叫仰角,
视线在水平线下方的角叫俯角
(3)方位角:从正北方向顺时针转到目标方向的夹角
(4)视角:由物体两端射出的两条
光线在眼球内交叉而成的角
(1)坡度:斜面与地平面所成的角度
题型一 不能到达两点间的距离问题
例1 如图, A,B两点都在河的对岸(不可到达),设计一种测量A,B 两点间的距离的方法.并求出A,B 间的距离。
跟踪训练1
题型二 测量高度问题
例2 如图,AB是底部B不可到达的一座建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法.并求出建筑物的高度。
跟踪训练2
题型三 测量角度问题
例3
跟踪训练3
实际问题
抽象概括
示意图
数学模型
推理
演算
数学模型的解
实际问题的解
还原说明
1.测量距离问题、高度问题、角度问题、面积问题、航海问题等实际应用解题思路:
四、课堂小结(2分钟)
五、当堂检测(14分钟)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
