华东师大版八年级下册数学 16.1.1 分式 课件(共17张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 16.1.1 分式 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 178.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
分式
创设情景:
请你来填一填:
(1)面积为2平方米的长方形一边长3米,则它的另一
边长为_______米;
(2)面积为S平方米的长方形一边长a米,则它的另一
边长为_______米;
(3)已知正方形的周长是 cm,则一边的长是____cm,
面积是_______cm2;
(4)一箱苹果售价P元,总重m千克,箱重n千克,则每
千克苹果的售价是______元.
分式的概念
问:在上面所列出的代数式中,哪些是整式?哪些不是?它们之间有什么区别?
探究归纳
分式的概念:即形如 (A、B是整式,
且B中含有字母,B≠0)的式子叫分式。
到本节课,我们一共学习了哪些代数式呢 请同学们讨论一下!
整式和分式统称为有理式。
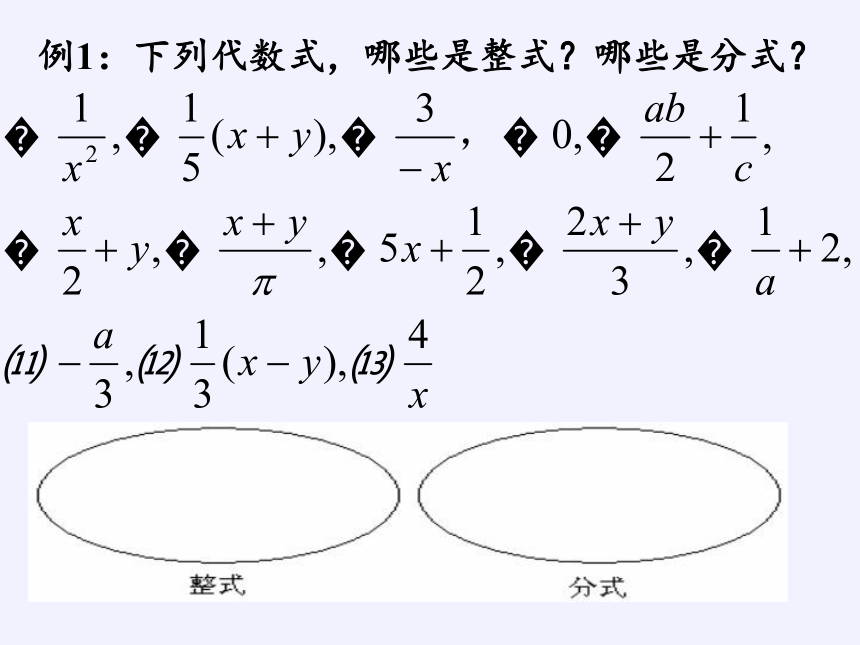
例1:下列代数式,哪些是整式?哪些是分式?
知识要点
1、判断一个有理式是不是分式,
关键看是否符合下式:
2、整式包括单项式和多项式,单个字母或数字是单项式。
整式与分式的识别
例2 (1)当x为何值时,分式 有意义
(2)当x为何值时,分式 有意义
例3 当x为何值时,分式 无意义
请你来做一做:
1、当x为何值时,代数式 有意义?
2、当x为何值时,分式 有意义?
3、当x为何值时,分式 有意义?
当x为何值时,上面这些代数式无意义呢
例4
当y取什么值时,分式 的值是零?
友情提示:
分式的定义
分式的意义
分式的值为0
分母≠0
①分子=0 ②代入分母≠0 ③最后答案
整式A、B相除可写为 的形式,若分母中含有字母,那么 叫做分式。
讨论:
若分式 的值为0,则x
的值是多少?
自主练习:
1、当x为何值时,代数式 有意义?
2、当x为何值时,分式 无意义?
3、当x为何值时,分式 的值为零?
4、x为何整数时,分式 的值为整数?
1、我们学习了什么新知识?
2、你有什么收获?
课后作业:
书 P5 习题17.1
第1、2、3题
谢 谢
分式
创设情景:
请你来填一填:
(1)面积为2平方米的长方形一边长3米,则它的另一
边长为_______米;
(2)面积为S平方米的长方形一边长a米,则它的另一
边长为_______米;
(3)已知正方形的周长是 cm,则一边的长是____cm,
面积是_______cm2;
(4)一箱苹果售价P元,总重m千克,箱重n千克,则每
千克苹果的售价是______元.
分式的概念
问:在上面所列出的代数式中,哪些是整式?哪些不是?它们之间有什么区别?
探究归纳
分式的概念:即形如 (A、B是整式,
且B中含有字母,B≠0)的式子叫分式。
到本节课,我们一共学习了哪些代数式呢 请同学们讨论一下!
整式和分式统称为有理式。
例1:下列代数式,哪些是整式?哪些是分式?
知识要点
1、判断一个有理式是不是分式,
关键看是否符合下式:
2、整式包括单项式和多项式,单个字母或数字是单项式。
整式与分式的识别
例2 (1)当x为何值时,分式 有意义
(2)当x为何值时,分式 有意义
例3 当x为何值时,分式 无意义
请你来做一做:
1、当x为何值时,代数式 有意义?
2、当x为何值时,分式 有意义?
3、当x为何值时,分式 有意义?
当x为何值时,上面这些代数式无意义呢
例4
当y取什么值时,分式 的值是零?
友情提示:
分式的定义
分式的意义
分式的值为0
分母≠0
①分子=0 ②代入分母≠0 ③最后答案
整式A、B相除可写为 的形式,若分母中含有字母,那么 叫做分式。
讨论:
若分式 的值为0,则x
的值是多少?
自主练习:
1、当x为何值时,代数式 有意义?
2、当x为何值时,分式 无意义?
3、当x为何值时,分式 的值为零?
4、x为何整数时,分式 的值为整数?
1、我们学习了什么新知识?
2、你有什么收获?
课后作业:
书 P5 习题17.1
第1、2、3题
谢 谢
