华东师大版七年级下册数学 10.3.1 图形的旋转 课件(共17张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 10.3.1 图形的旋转 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 468.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 14:26:25 | ||
图片预览




文档简介
(共17张PPT)
图形的旋转
这些情境中的转动现象,有什么共同特征?
它们有共同点吗
荡秋千
B
O
A
45
0
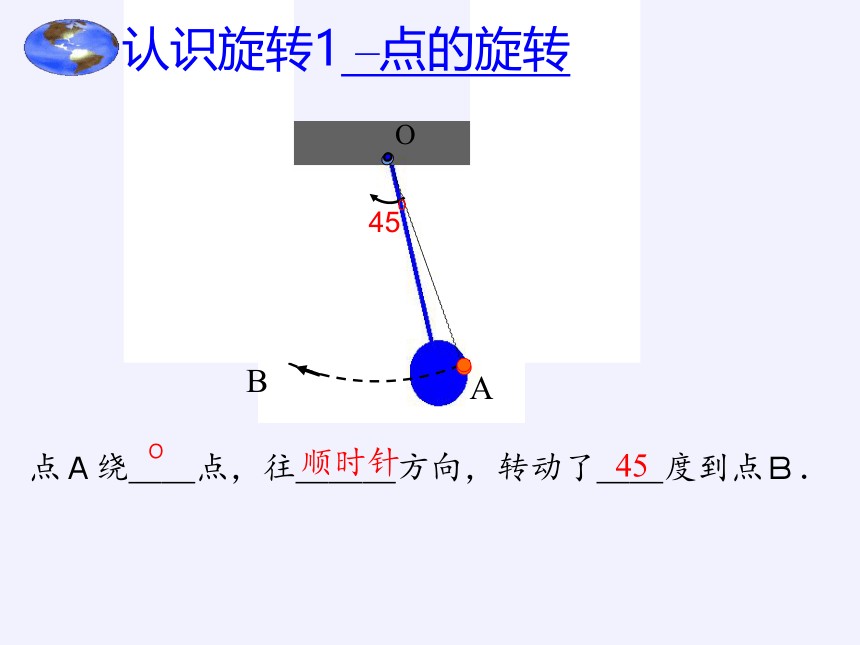
点A绕__点,往___方向,转动了__度到点B.
O
顺时针
45
认识旋转1 –点的旋转
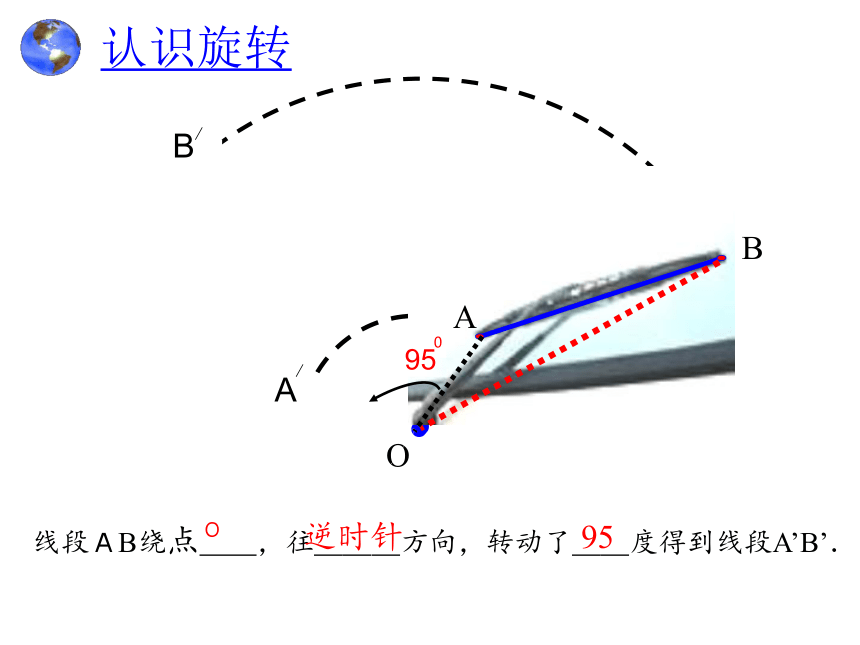
认识旋转
O
B
A
B
/
A
/
95
0
线段AB绕点__,往___方向,转动了__度得到线段A’B’.
O
逆时针
95
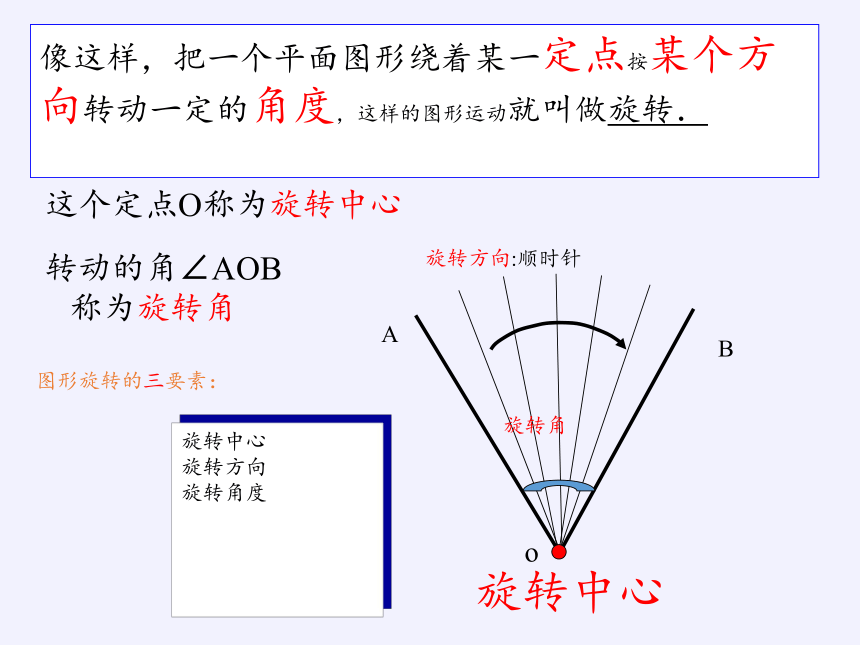
这个定点O称为旋转中心
旋转角
旋转中心
像这样,把一个平面图形绕着某一定点按某个方向转动一定的角度,这样的图形运动就叫做旋转.
A
o
B
转动的角∠AOB
称为旋转角
图形旋转的三要素:
旋转方向:顺时针
旋转中心
旋转方向
旋转角度
试一试
点B的对应点是________;
线段OB的对应线段是________;
线段AB的对应线段是________;
∠A的对应角是________;
∠B的对应角是________;
旋转中心是________;
旋转方向是_________________;
如图,△AOB绕点O旋转得到△ A′ O B′,则:
点B′
线段OB′
线段A′B′
∠A′
∠ B′
点O
∠AO A′
﹑∠BO B′
旋转角是_________________;
旋转角度是_________________;
逆时针
45°
做一做
如右图,如果旋转中心在△ABC外的点O处,逆时针旋转60°,将△ABC旋转到△A′B′C′的位置,那么这两个三角形的顶点、边与角是如何对应的呢?
例1、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3) 如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
解:(1)旋转中心是A。
(2)旋转了60°。
(3)点M转到了AC 的中点位置上。
图10.3.6
例2、如图,点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90,旋转后的线段与原线段的位置有何关系?,如果逆时针方向旋转90呢?
解: 如图(2),顺时针旋转90°, A′B′与AB互相垂直。
如图(3),逆时针旋转90°, A′′B′′与AB互相垂直。
小结: 线段旋转90°后与原来位置的线段互相垂直。
1.下列现象中,属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动; ⑥荡秋千运动.
A.2 B.3 C.4 D.5
小试牛刀:
C
______________
(A)
(B)
(C)
2.观察变化规律,第四幅应该是哪个图形。
C
知识小结
1、旋转的定义
2、旋转的三要素:
①旋转中心.
②旋转方向.
③旋转角度.
A
B
C
D
E
F
·
O
能力提升1
如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
3
2、如图将△ABC绕C点逆时针旋转30°后,点B落在B′,点A落在A’点位置,若A’C⊥AB,则∠B’A’C=_____。
600
能力提升2
作业
教材P121 2、3
谢 谢
图形的旋转
这些情境中的转动现象,有什么共同特征?
它们有共同点吗
荡秋千
B
O
A
45
0
点A绕__点,往___方向,转动了__度到点B.
O
顺时针
45
认识旋转1 –点的旋转
认识旋转
O
B
A
B
/
A
/
95
0
线段AB绕点__,往___方向,转动了__度得到线段A’B’.
O
逆时针
95
这个定点O称为旋转中心
旋转角
旋转中心
像这样,把一个平面图形绕着某一定点按某个方向转动一定的角度,这样的图形运动就叫做旋转.
A
o
B
转动的角∠AOB
称为旋转角
图形旋转的三要素:
旋转方向:顺时针
旋转中心
旋转方向
旋转角度
试一试
点B的对应点是________;
线段OB的对应线段是________;
线段AB的对应线段是________;
∠A的对应角是________;
∠B的对应角是________;
旋转中心是________;
旋转方向是_________________;
如图,△AOB绕点O旋转得到△ A′ O B′,则:
点B′
线段OB′
线段A′B′
∠A′
∠ B′
点O
∠AO A′
﹑∠BO B′
旋转角是_________________;
旋转角度是_________________;
逆时针
45°
做一做
如右图,如果旋转中心在△ABC外的点O处,逆时针旋转60°,将△ABC旋转到△A′B′C′的位置,那么这两个三角形的顶点、边与角是如何对应的呢?
例1、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3) 如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
解:(1)旋转中心是A。
(2)旋转了60°。
(3)点M转到了AC 的中点位置上。
图10.3.6
例2、如图,点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90,旋转后的线段与原线段的位置有何关系?,如果逆时针方向旋转90呢?
解: 如图(2),顺时针旋转90°, A′B′与AB互相垂直。
如图(3),逆时针旋转90°, A′′B′′与AB互相垂直。
小结: 线段旋转90°后与原来位置的线段互相垂直。
1.下列现象中,属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动; ⑥荡秋千运动.
A.2 B.3 C.4 D.5
小试牛刀:
C
______________
(A)
(B)
(C)
2.观察变化规律,第四幅应该是哪个图形。
C
知识小结
1、旋转的定义
2、旋转的三要素:
①旋转中心.
②旋转方向.
③旋转角度.
A
B
C
D
E
F
·
O
能力提升1
如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
3
2、如图将△ABC绕C点逆时针旋转30°后,点B落在B′,点A落在A’点位置,若A’C⊥AB,则∠B’A’C=_____。
600
能力提升2
作业
教材P121 2、3
谢 谢
