4.7生产和生活中的机械能守恒同步练习
文档属性
| 名称 | 4.7生产和生活中的机械能守恒同步练习 |  | |
| 格式 | doc | ||
| 文件大小 | 436.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-24 14:14:22 | ||
图片预览



文档简介
4.7生产和生活中的机械能守恒
一、选择题(共15题)
1.在一个与外界没有热交换的房间里打开冰箱门,冰箱正常工作,过一段时间房间内的温度将如何变化
A.降低 B.升高 C.不变 D.无法确定
2.2020年2月2日上午,武汉火神山医院正式交付,从方案设计到建成交付仅用10天,被誉为“中国速度”。在医院建造过程中,有一吊机将静止在地面上的货物竖直向上吊起,货物由地面运动至最高点的过程中,v-t图像如图所示。下列判断正确的是 ( )
A.1s末货物的加速度大小为1.5m/s2
B.前内货物克服重力做功的功率不变
C.最后内货物处于超重状态
D.在第末至第末的过程中,货物的机械能增大
3.如图所示,一个质量为m的物体(可视为质点)以某一速度从A点冲上倾角为的固定斜面,其运动的加速度大小为,该物体在斜面上上升的最大高度为h,则在这个过程中物体的( )
A.整个过程中物体机械能守恒 B.重力势能增加了
C.动能损失了 D.机械能损失了
4.如图甲所示,物体以一定初速度从倾角a= 37°的斜面底端沿斜面向上运动,上升的最大高度为3.0 m,选择地面为零势能参考平面,上升过程中,物体的机械能E机随上升高度h的变化如图乙所示.(g=" 10" m/s2,sin 37°= 0. 6 ,cos37°= 0. 8).下列说法中正确的是( )
A.物体回到斜面底端时的动能Ek=" 10" J B.物体的质量m=" 10" kg
C.物体上升过程的加速度大小a=15m/s2 D.物体可能静止在斜面顶端
5.一升降机箱底部装有若干个弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦和空气阻力影响,则升降机在从弹簧下端触地直到最低点的一段运动过程中
A.升降机的速度不断减小
B.升降机的加速度不断变大
C.先是弹力做的负功大于重力做的正功,然后是弹力做的负功小于重力做的正功
D.先是弹力做的负功小于重力做的正功,然后是弹力做的负功大于重力做的正功
6.某足球守门员将一足球从自己的球门前大脚踢向对方场地,足球从踢出到落地的整过运动轨迹如下图所示(假设足球在运动过程中没被其他运动员截住),图中的甲、乙、丙是足球轨迹上的三个点,其中甲与丙是等高点,图中“1”“2”是足球的起点或落地点,下列说法正确的是( )
A.足球在运动过程中机械能守恒
B.足球从1到乙的时间小于从乙到2的时间
C.足球的起点位置是2点
D.足球从1到乙的过程中动能的变化量等于足球从乙到2的过程动能的变化量
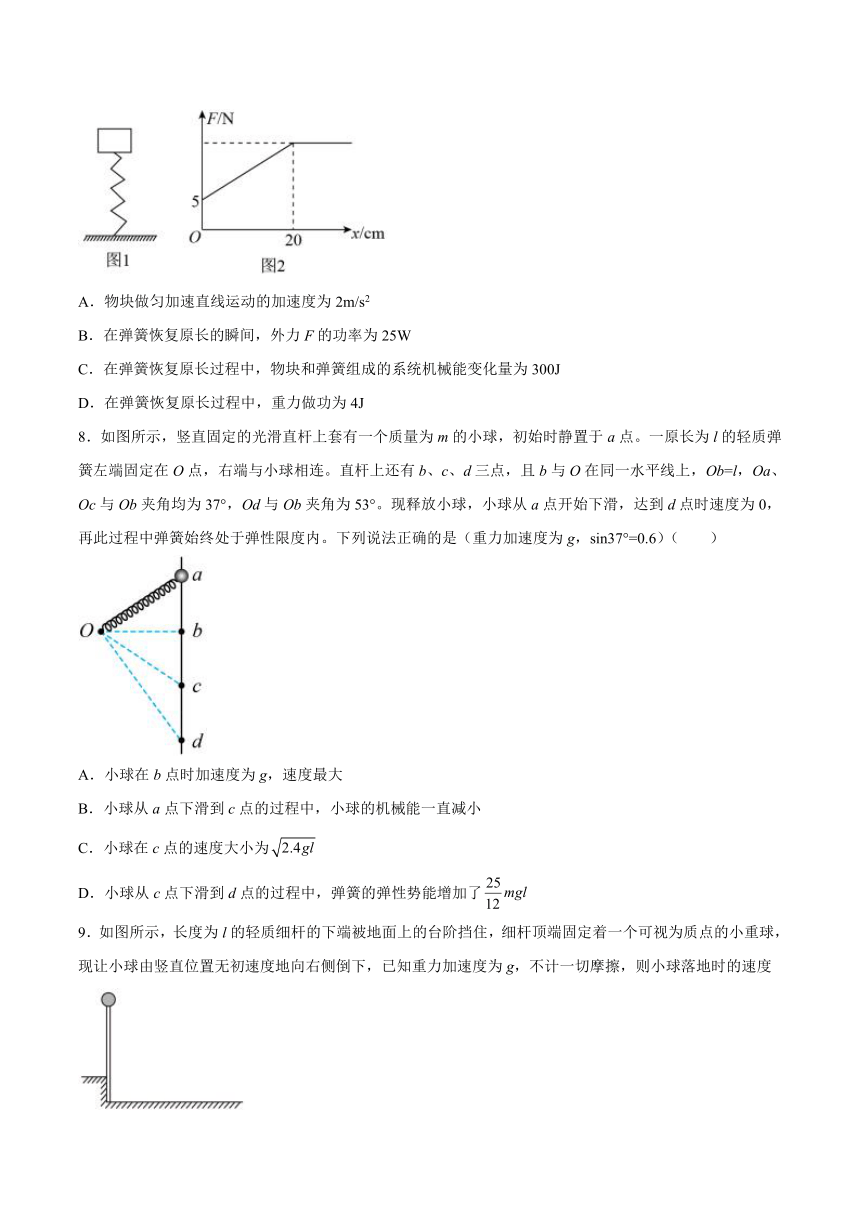
7.如图1所示,竖直放置的轻弹簧下端固定在地上,上端与质量为m的物块相连(不栓接)初始状态处于静止状态。现对物块施加竖直向上的外力F使物块做匀加速直线运动,经过0.4s弹簧恢复原长,图2是力F随物块位移x变化的图像,重力加速度g取10m/s2。下列说法正确的是( )
A.物块做匀加速直线运动的加速度为2m/s2
B.在弹簧恢复原长的瞬间,外力F的功率为25W
C.在弹簧恢复原长过程中,物块和弹簧组成的系统机械能变化量为300J
D.在弹簧恢复原长过程中,重力做功为4J
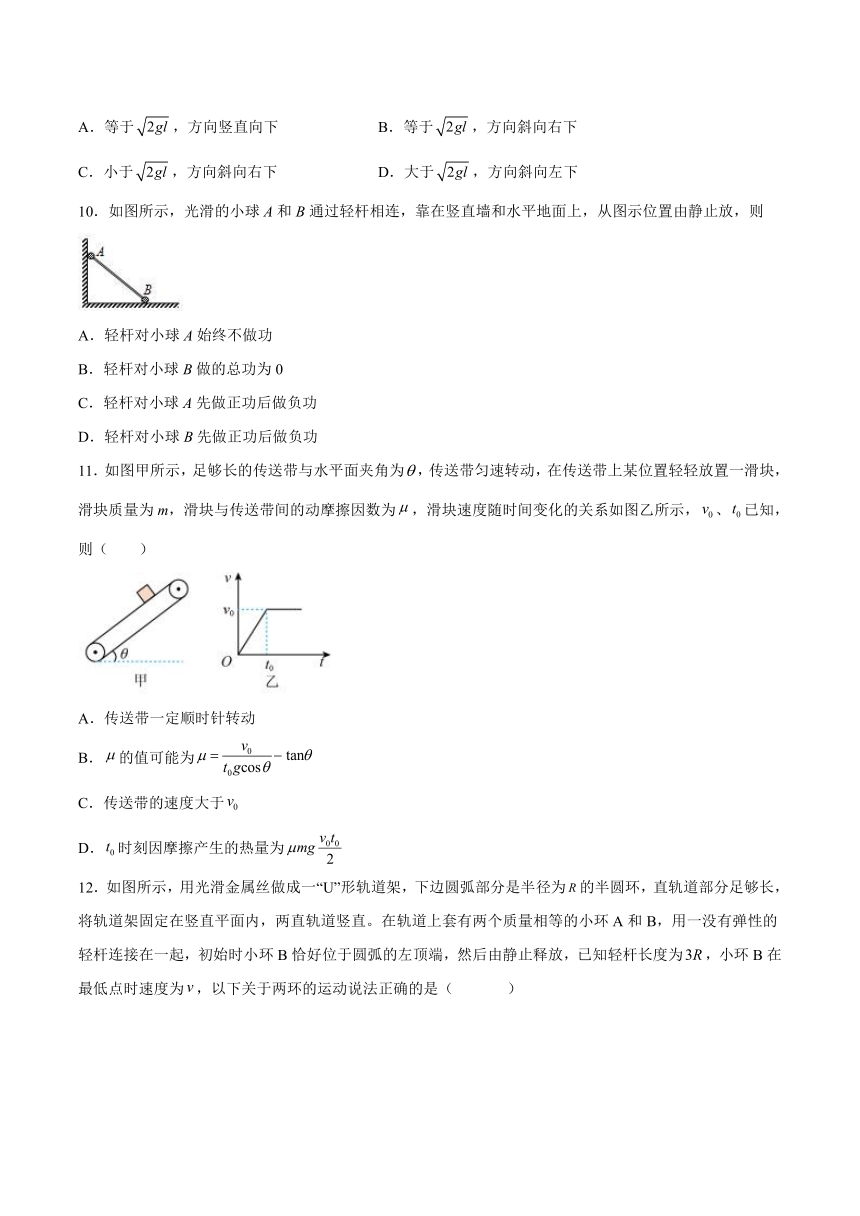
8.如图所示,竖直固定的光滑直杆上套有一个质量为m的小球,初始时静置于a点。一原长为l的轻质弹簧左端固定在O点,右端与小球相连。直杆上还有b、c、d三点,且b与O在同一水平线上,Ob=l,Oa、Oc与Ob夹角均为37°,Od与Ob夹角为53°。现释放小球,小球从a点开始下滑,达到d点时速度为0,再此过程中弹簧始终处于弹性限度内。下列说法正确的是(重力加速度为g,sin37°=0.6)( )
A.小球在b点时加速度为g,速度最大
B.小球从a点下滑到c点的过程中,小球的机械能一直减小
C.小球在c点的速度大小为
D.小球从c点下滑到d点的过程中,弹簧的弹性势能增加了
9.如图所示,长度为l的轻质细杆的下端被地面上的台阶挡住,细杆顶端固定着一个可视为质点的小重球,现让小球由竖直位置无初速度地向右侧倒下,已知重力加速度为g,不计一切摩擦,则小球落地时的速度
A.等于,方向竖直向下 B.等于,方向斜向右下
C.小于,方向斜向右下 D.大于,方向斜向左下
10.如图所示,光滑的小球A和B通过轻杆相连,靠在竖直墙和水平地面上,从图示位置由静止放,则
A.轻杆对小球A始终不做功
B.轻杆对小球B做的总功为0
C.轻杆对小球A先做正功后做负功
D.轻杆对小球B先做正功后做负功
11.如图甲所示,足够长的传送带与水平面夹角为,传送带匀速转动,在传送带上某位置轻轻放置一滑块,滑块质量为m,滑块与传送带间的动摩擦因数为,滑块速度随时间变化的关系如图乙所示,、已知,则( )
A.传送带一定顺时针转动
B.的值可能为
C.传送带的速度大于
D.时刻因摩擦产生的热量为
12.如图所示,用光滑金属丝做成一“U”形轨道架,下边圆弧部分是半径为的半圆环,直轨道部分足够长,将轨道架固定在竖直平面内,两直轨道竖直。在轨道上套有两个质量相等的小环A和B,用一没有弹性的轻杆连接在一起,初始时小环B恰好位于圆弧的左顶端,然后由静止释放,已知轻杆长度为,小环B在最低点时速度为,以下关于两环的运动说法正确的是( )
A.B在圆弧底部时动能最大 B.A下落的最大距离为
C.B在圆弧底部时机械能最大 D.小环B在最低点时A的速度为
13.图中,甲、乙两球质量相同,轻质悬线长度L甲>L乙,悬点等高。先将悬线拉至水平位置,再无初速地释放两球,设甲球通过最低点时的动能为Ek甲,此时悬线的拉力为F甲,甲球的向心加速度为a甲,乙球通过最低点时的动能为Ek乙,此时悬线的拉力为F乙,乙球的向心加速度为a乙,则下列结论中正确的是( )
A.Ek甲>Ek乙
B.F甲>F乙
C.a甲=a乙
D.相对于同一参考平面,甲球到达最低点时的机械能小于乙球到达最低点的机械能
14.如图所示,高的斜面固定不动。一个质量的物体,由静止开始从斜面的顶点滑下,滑到斜面底端时的速度大小为,g取,在此过程中,下列判断正确的是( )
A.系统的机械能保持不变 B.物体的重力势能减少了25J
C.物体的动能增加了18J D.物体的机械能减少了7J
15.如图所示,有两个物块A和,质量分别为和,用同一根轻质细线将两个物块连接在滑轮组上,滑轮质量不计,不计一切摩擦及空气阻力,重力加速度为g,现将两物块由静止释放,经过一段时间,A的位移为,在此过程中,下列说法正确的( )
A.物块A和总势能保持不变 B.A的位移为时,的速度为
C.细线的拉力大小为 D.A和重力的功率大小之比为1:3
二、填空题
16.劲度系数为k的轻弹簧一端固定在墙上,另一端与质量为m的物体相连,物体与桌面间的摩擦因数为μ.初始时刻物体静止,弹簧为自然长度.若向右以恒力F(F>μmg)拉物体,则该物体能够到达的最远位置与初始位置的距离为_____.
17.质量的小球系于弹簧的一端,套在光滑竖直圆环上,弹簧的另一端固定在环上的A点,环半径,弹簧原长。当球从图中位置C滑至最低点B时,测得,则在B点时弹簧的弹性势能______。
18.将一小球竖直向上抛出,若小球的速度越大空气阻力越大,那么,小球在先上升后下降的过程中,它的机械能___________,它受的合力___________。(选填“变大”、“不变”、“变小”)。
19.如图所示,在倾角为30°的斜面上,以3J的动能水平抛出一物体,当这个物体落到斜面上某一点时,它的动能为____________J。
三、综合题
20.如图所示,将倾角θ=30°、表面粗糙的斜面固定在地面上,用一根轻质细绳跨过两个光滑的半径很小的滑轮连接甲、乙两物体(均可视为质点),把甲物体放在斜面上且细绳与斜面平行,把乙物体悬在空中,并使细绳拉直且偏离竖直方向α=60°。开始时甲、乙均静止。现同时释放甲、乙两物体,乙物体将在竖直平面内往返运动,测得绳长OA为l=0.5m,当乙物体运动经过最高点和最低点时,甲物体在斜面上均恰好未滑动,已知乙物体的质量为 m=1kg,忽略空气阻力,取重力加速度g=10m/s2,求:
(1)乙物体在竖直平面内运动到最低点时的速度大小以及所受的拉力大小
(2)甲物体的质量以及斜面对甲物体的最大静摩擦力的大小
(3)斜面与甲物体之间的动摩擦因数μ(设最大静摩擦力等于滑动摩擦力)
21.如图所示,两个半径均为R的光滑圆弧形轨道竖直放置,圆心在同一高度,一倾角为37°的固定光滑斜面与两圆弧轨道相切于C、D(斜面与左侧圆弧轨道的缝隙可以忽略不计),一质量为m的物块(可看成质点)放在光滑水平面的A点,左侧圆弧轨道与水平轨道相切.已知sin37°=0.6,cos37°=0.8.
(1)要使物块能到达E点,则物块在A点的初速度至少多大
(2)若物块在A点的初速度为,求物块从E点抛出后到落到斜面上所用的时间.
22.如图所示,半径的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A。一质量的小球,以初速度在水平地面上向左作匀减速直线运动,球与粗糙水平地面间的动摩擦因数,运动4m后,冲上竖直半圆环,经过最高点B最后小球落在C点。取重力加速度。求:
(1)小球到达A点时速度大小?
(2)小球经过B点时对轨道的压力大小?
(3)A、C两点间的距离?
23.如图所示,质量均为m=0.5 kg的A、B两小物块用轻质弹簧相连,竖直静止放置在水平地面上,弹簧的劲度系数为k=0.5 N/cm,B物块上系一根轻绳,轻绳绕过固定光滑的定滑轮与水平面上的C物块相连,C物块的质量为M=1 kg,与水平面间的动摩擦因数为0.2,初始时轻绳伸直但无拉力。用一水平向右的拉力F作用在C物块上,使C物块向右做匀加速直线运动,1s时A物块恰好离开地面,重力加速度大小g=10 m/s2,求:
(1)A物块刚好离开地面时,水平拉力F的大小;
(2)A物块刚好离开地面前,水平拉力F做功的大小。
试卷第1页,共3页
参考答案:
1.B
【详解】
冰箱消耗电能使冰箱内外发生热交换而达到内部制冷,把冰箱与房间看成一个系统,打开冰箱门后,冰箱与房间内的热交换发生在系统内,系统内部无法使系统总能量发生变化。但系统消耗电能增加了系统的总能量,根据能量守恒定律,系统增加的能量转化为内能使房间的温度升高。
故选B。
2.D
【详解】
A.1s末货物的加速度大小为
选项A错误;
B.根据
P=mgv
可知,前2s内货物克服重力做功的功率不断增加,选项B错误;
C.最后内货物向上减速,加速度向下,处于失重状态,选项C错误;
D.在第4s末至第7s末的过程中,拉力向上做正功,则货物的机械能增大,选项D正确。
故选D。
3.D
【详解】
A.由牛顿第二定律得
mgsin30°+f=m×0.6g
解得摩擦力
f=0.1mg
此过程有摩擦力做功,机械能不守恒,故A错误;
B.物体在斜面上能够上升的最大高度为h,所以重力势能增加了 EP=mgh,故B错误;
C.由动能定理可知,动能损失量为合外力做的功的大小,即
Ek=F合 s=m×0.6g×2h=1.2mgh
故C错误;
D.由功能关系知,机械能的损失量为
E=fs=0.1mg×2h=0.2mgh
故D正确。
故选D。
4.A
【详解】
试题分析:根据功能原理得,物体上升过程中摩擦力做功为:Wf=E2-E1=30J-50J=-20J,在整个过程中由动能定理得:EK-EK0=2Wf则有:EK=EK0+2W=50+2×(-20)=10J,故A正确;物体到达最高点时,机械能为:E=EP=mgh,由图知:EP=30J.得:,故B错误;物体上升过程中,克服摩擦力做功,机械能减少,减少的机械能等于克服摩擦力的功,,即:,得:μ=0.5;物体上升过程中,由牛顿第二定律得:mgsinα+μmgcosα=ma,得:a=gsinα+μgcosα=10×0.6+0.5×10×0.8=10m/s2,故C错误;因为mgsinα>μmgcosα,所以物体不可能静止在斜面顶端.故D错误.故选A.
5.D
【详解】
升降机在从弹簧下端触地后直到最低点的一段运动过程中,开始阶段,重力大于弹力,加速度方向向下,向下做加速运动,当重力和弹力相等后,弹力大于重力,加速度方向向上,向下做减速运动,加速度的大小先减小后增大,速度先增大后减小.故A、B错误.升降机在从弹簧下端触地直到最低点的一段运动过程中,在弹力等于重力之前时,速度在不断增加,则弹力做的负功小于重力所作的正功;在弹力等于重力之后时,速度不断减小,则弹力做的负功大于重力做的正功.故C错误,D正确.故选D.
6.B
【详解】
A.由轨迹图和斜抛运动知识可知,如果足球机械能守恒的话,其轨迹是对称的,由此可知足球在运动过程中受到空气的阻力,故选项A错误;
B.根据
(表示竖直方向的分加速度)
在竖直方向上,足球从1到乙的过程,空气阻力向下
从乙到2的过程空气阻力向上
所以上升过程的时间小于下落过程的时间,故B正确;
C.由于足球受到空气的阻力,故在水平方向的分速度会减小,故足球的起点位置是“1”,故选项C错误;
D.足球在落点的速度小于在起点的速度,根据
可知选项D错误。
故选B。
7.B
【详解】
A.由图2可知,在弹簧恢复原长过程,物块的位移是0.2m,根据
可知做匀加速直线运动的加速度
A错误;
B.初始状态物块处于静止状态有
mg=k△x
加外力瞬间根据牛顿第二定律有
F+k△x-mg=ma
弹簧弹力不能突变,因此有
F=ma
解得
m=2kg
k=100N/m
在弹簧恢复原长瞬间,有
F1-mg=ma
得弹簧恢复原长瞬间弹力
F1=25N
此时刻物块的速度
v=at=1m/s
所以外力F的功率为
P=Fv=25W
B正确;
C.物块和弹簧组成系统的机械能变化量等于外力F做功,在弹簧恢复原长过程中,外力F做功是图2梯形面积,为3J。C错误;
D.在弹簧恢复原长过程中,重力做功
WG=-mgh=-4J
D错误。
故选B。
8.D
【详解】
A.从a到b,弹簧对滑块由沿弹簧向下的拉力,滑块的速度不断增大;从b到c,弹簧对滑块有沿弹簧向上的拉力,开始时拉力沿杆向上的分力小于滑块的重力,滑块仍然在加速,所以滑块在b点时速度不是最大,此时合力为mg,则加速度为g, A错误;
B.从a下滑到c的过程中,对小球和弹簧的系统机械能守恒,由于弹性势能先减小后增加,则小球的机械能先增大后减小, B错误;
C.小球从a点下滑到c点的过程中,由小球和弹簧的系统机械能守恒得
可得滑块在c点的速度大小为
C错误;
D.小球从c点下滑到d点的过程中,小球的机械能减少量等于弹簧弹性势能增加量
解得
D正确。
故选D。
9.B
【详解】
小球在最高点时,速度为0,对杆有压力;设细杆下端被铰链固定,则小球落至水平地面时,细杆中有拉力,由此可知,小球在之前某个时刻就开始对杆有向外的拉力,而本题中细杆下端没有被固定,则小球在这个时刻开始将带着细杆脱离圆周轨道而做斜抛运动,故落地速度斜向右下;由机械能守恒,可知小球落地时的速度大小等于。故ACD错误,B正确。
故选择B。
10.D
【详解】
AB.从A开始下滑到落地的整个过程中,根据功能关系可知,小球A的重力势能转化为AB的动能,对B分析可知,杆对小球B做的功等于B的动能增量,故杆对B做正功;再对A分析可知,A的机械能转移到B上面,故整个过程中杆对A的弹力做负功;故AB错误;
CD.将A球速度分解成沿着杆与垂直于杆方向,同时B球速度也是分解成沿着杆与垂直于杆两方向.
则有,A球:
v⊥=vAsinα
v∥=vAcosα
而B球
v′⊥=vBsinβ
v′∥=vBcosβ
α+β=90°
由于同一杆,则有
vAcosα=vBsinα
则可知,当α达到45°后,B的速度将减小,轻杆做负功;同理轻杆对A做正功;由以上分析可知,轻杆对小球A先做负功再做正功;而轻杆对小球B先做正功再做负功,故C错误,D正确.
故选D.
11.B
【详解】
由图乙所示图象可知,滑块先做初速度为零的匀加速直线运动,在t0后以速度v0做匀速直线运动;由此可知
mgsinθ≤μmgcosθ
如果
mgsinθ>μmgcosθ
滑块在传送带上不会做匀速直线运动;
AC.如果传送带沿逆时针方向转动,滑块放在传送带上后受到的滑动摩擦力沿传送带向下,滑块先做匀加速直线运动,当滑块速度与传送带速度相等时滑块做匀速直线运动,则传送带的速度:v=v0;如果传送带沿顺时针方向转动,滑块刚放在传送带上时受到的滑动摩擦力沿斜面向上,滑块向上做匀加速直线运动,当滑块速度与传送带速度相等时滑块做匀速直线运动,传送带速度:v=v0;传送带速度不会大于v0,传送带即可能沿顺时针也可能沿逆时针方向转动,故AC错误;
B.由图乙所示图象可知,滑块做匀加速直线运动时的加速度
如果传送带沿逆时针方向转动,由牛顿第二定律得
mgsinθ+μmgcosθ=ma
解得
故B正确;
D.在t0时间内物块相对传送带的位移
则摩擦生热
选项D错误。
故选B。
12.B
【详解】
C.根据题意可知,系统机械能守恒,由于杆的长度大于圆弧部分的直径,所以只有环B可以到达轨道右侧,而环A只能在左侧轨道上运动,当杆经过圆弧的圆心位置时,B的机械能最大,A的速度为零,由几何关系可知,选项B正确,C错误;
A.B在最低点右侧某位置重力沿圆弧切线方向的分量与杆的作用力沿圆弧切线方向的分量相等时速度最大,A错误;
D.当环B进入圆弧轨道时两环在沿杆方向的速度分量相同,设B在最低点时A速度为,B的速度为,杆与竖直方向夹角为,如图所示:
有
由几何关系知
又
则A的速度为
选项D错误。
故选B。
13.AC
【详解】
A.根据机械能守恒定律可知
Ek=mgL
可知Ek甲>Ek乙,A正确;
B.根据动能定理得
到达最低点的速度为
在最低点据牛顿第二定律可得
联立解得悬线的拉力为
F=3mg
与悬线长度无关,B错误;
C.结合B的解析可得,向心力加速度为
C正确;
D.相对于同一参考平面,因为两球开始的机械能相同,故甲球到达最低点时的机械能等于乙球到达最低点的机械能,D错误。
故选AC。
14.BCD
【详解】
AD.从顶端到底端,系统的机械能损失
则机械能不守恒,选项A错误,D正确;
B.物体的重力势能减少了
选项B正确;
C.物体的动能增加了
选项C正确;
故选BCD。
15.BC
【详解】
A.根据机械能守恒定律可知,B减小的重力势能全部转化为A的重力势能和两物体的动能,所以,A和B的重力势能之和减小,故A错误;
B.设A上升到h位置时的速度为v1,B的速度为v2,根据动滑轮的特点可知
v2=2v1
根据A和B组成的系统机械能守恒可得
联立解得
故B正确;
C.根据动滑轮的特点可知,A的加速度为B的加速度的一半,根据牛顿第二定律可得,对A有
对B有
又有
a2=2a1
联立解得,轻绳的拉力大小
故C正确;
D.重力功率
由于v2=2v1, ,故A和重力的功率大小之比为1:4,故D错误。
故选BC。
16.
【详解】
设该物体能够到达的最远位置与初始位置的距离为x.根据功能关系得:
Fx=μmgx+
解得:x=(F﹣μmg)
17.15J
【详解】
从C到B过程,据机械能守恒可得
代入数据解得。
18. 变小 变小
【详解】
竖直向上抛出的小球,离开手后会继续向上运动,若考虑空气阻力,小球与空气摩擦,一部分机械能转化为内能,故机械能的总量变小;
小球上升时,受到重力与空气阻力作用,做减速运动,由于二者方向相同,所以合力为二力之和,即
速度减小,阻力减小,则合力减小,到最高点时速度为0,阻力为0,合力为;小球下降时,做加速度运动,由于阻力方向与重力相反,所以合力为二力之差,即
由于小球的速度变大,空气阻力变大,则合力会继续减小,故在整个过程中,小球所受合力越来越小。
19.7
【详解】
设物体的质量为m,初速度为v0,抛出点到落点的高度差为h,水平距离为s,则有
h=stan30°
由平抛运动规律可得
s=v0t
解得
以落点所在平面为参考平面,根据机械能守恒定律得
则
20.(1)2.24 m/s,20 N;(2)2.5 kg,7.5 N;(3)0.35
【详解】
(1)当乙物体运动到最低点时,绳子上的拉力最大,设为F1,对乙物体,由动能定理得
mgl(1-cosα)=
又由牛顿第二定律得
F1-mg=
乙物体在竖直平面内运动到最低点时
v=m/s=2.24m/s?
乙物体运动到最低点时所受的拉力F
F1=20 N
(2)当乙物体运动到最高点时,绳子上的拉力最小,设为F2,此时乙物体向心力为0,即
F2=mgcosα
此时甲物体恰好不下滑,有
Mgsinθ=Ff+F2
乙物体到最低点时,甲物体恰好不上滑,则有
Mgsinθ+Ff=F1
联立解得
M=2.5kg
Ff=7.5 N?
(3)对甲物体,有
Ff=μFN
FN=Mgcosθ
联立解得
μ==0.35
21.(1); (2)
【详解】
解:(1)若斜面是光滑的,物块沿轨道运动过程机械能守恒,设物切到E点时速度为v1,由牛顿第二定律则有
由机械能守恒定律得
在E点有:F≥0
解得
即初速度至少为。
(2)若初速度为,斜面光滑,设物块到E点的速度为,则有
解得
从E点拋出,物块做平抛运动,由平抛运动规律可有
由几何关系有
计算的结果为
22.(1);(2);(3)
【详解】
(1)设小球运动长度到达A点,小球从开始运动到A点过程中,由动能定理得
代入数据解得
(2)从A到B过程小球机械能守恒,由机械能守恒定律得
解得
在B点,由牛顿第二定律得
代入数据解得
由牛顿第三定律可知,小球对轨道的压力
(3)小球离开B点后做平抛运动,竖直方向
水平方向
代入数据联立解得
23.(1) F=12.6 N (2) WF=1.52 J
【详解】
(1)初始时,弹簧的压缩量为
A物块刚好离开地面时,弹簧的伸长量为
从初始位置到A物块刚好离开地面的过程,B物块和C物块的位移均为
C物块做匀加速直线运动,有
A物块刚好离开地面时,弹簧弹力大小为mg,对B物块,有
对C物块,有
代入数据解得
(2)当A物块刚好离开地面时,B、C物块的速度大小均为
初始位置时与A物块刚好离开地面时,弹簧的弹性势能相等,对B、C物块与弹簧组成的系统,由功能关系可得
代入数据解得
答案第1页,共2页
一、选择题(共15题)
1.在一个与外界没有热交换的房间里打开冰箱门,冰箱正常工作,过一段时间房间内的温度将如何变化
A.降低 B.升高 C.不变 D.无法确定
2.2020年2月2日上午,武汉火神山医院正式交付,从方案设计到建成交付仅用10天,被誉为“中国速度”。在医院建造过程中,有一吊机将静止在地面上的货物竖直向上吊起,货物由地面运动至最高点的过程中,v-t图像如图所示。下列判断正确的是 ( )
A.1s末货物的加速度大小为1.5m/s2
B.前内货物克服重力做功的功率不变
C.最后内货物处于超重状态
D.在第末至第末的过程中,货物的机械能增大
3.如图所示,一个质量为m的物体(可视为质点)以某一速度从A点冲上倾角为的固定斜面,其运动的加速度大小为,该物体在斜面上上升的最大高度为h,则在这个过程中物体的( )
A.整个过程中物体机械能守恒 B.重力势能增加了
C.动能损失了 D.机械能损失了
4.如图甲所示,物体以一定初速度从倾角a= 37°的斜面底端沿斜面向上运动,上升的最大高度为3.0 m,选择地面为零势能参考平面,上升过程中,物体的机械能E机随上升高度h的变化如图乙所示.(g=" 10" m/s2,sin 37°= 0. 6 ,cos37°= 0. 8).下列说法中正确的是( )
A.物体回到斜面底端时的动能Ek=" 10" J B.物体的质量m=" 10" kg
C.物体上升过程的加速度大小a=15m/s2 D.物体可能静止在斜面顶端
5.一升降机箱底部装有若干个弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦和空气阻力影响,则升降机在从弹簧下端触地直到最低点的一段运动过程中
A.升降机的速度不断减小
B.升降机的加速度不断变大
C.先是弹力做的负功大于重力做的正功,然后是弹力做的负功小于重力做的正功
D.先是弹力做的负功小于重力做的正功,然后是弹力做的负功大于重力做的正功
6.某足球守门员将一足球从自己的球门前大脚踢向对方场地,足球从踢出到落地的整过运动轨迹如下图所示(假设足球在运动过程中没被其他运动员截住),图中的甲、乙、丙是足球轨迹上的三个点,其中甲与丙是等高点,图中“1”“2”是足球的起点或落地点,下列说法正确的是( )
A.足球在运动过程中机械能守恒
B.足球从1到乙的时间小于从乙到2的时间
C.足球的起点位置是2点
D.足球从1到乙的过程中动能的变化量等于足球从乙到2的过程动能的变化量
7.如图1所示,竖直放置的轻弹簧下端固定在地上,上端与质量为m的物块相连(不栓接)初始状态处于静止状态。现对物块施加竖直向上的外力F使物块做匀加速直线运动,经过0.4s弹簧恢复原长,图2是力F随物块位移x变化的图像,重力加速度g取10m/s2。下列说法正确的是( )
A.物块做匀加速直线运动的加速度为2m/s2
B.在弹簧恢复原长的瞬间,外力F的功率为25W
C.在弹簧恢复原长过程中,物块和弹簧组成的系统机械能变化量为300J
D.在弹簧恢复原长过程中,重力做功为4J
8.如图所示,竖直固定的光滑直杆上套有一个质量为m的小球,初始时静置于a点。一原长为l的轻质弹簧左端固定在O点,右端与小球相连。直杆上还有b、c、d三点,且b与O在同一水平线上,Ob=l,Oa、Oc与Ob夹角均为37°,Od与Ob夹角为53°。现释放小球,小球从a点开始下滑,达到d点时速度为0,再此过程中弹簧始终处于弹性限度内。下列说法正确的是(重力加速度为g,sin37°=0.6)( )
A.小球在b点时加速度为g,速度最大
B.小球从a点下滑到c点的过程中,小球的机械能一直减小
C.小球在c点的速度大小为
D.小球从c点下滑到d点的过程中,弹簧的弹性势能增加了
9.如图所示,长度为l的轻质细杆的下端被地面上的台阶挡住,细杆顶端固定着一个可视为质点的小重球,现让小球由竖直位置无初速度地向右侧倒下,已知重力加速度为g,不计一切摩擦,则小球落地时的速度
A.等于,方向竖直向下 B.等于,方向斜向右下
C.小于,方向斜向右下 D.大于,方向斜向左下
10.如图所示,光滑的小球A和B通过轻杆相连,靠在竖直墙和水平地面上,从图示位置由静止放,则
A.轻杆对小球A始终不做功
B.轻杆对小球B做的总功为0
C.轻杆对小球A先做正功后做负功
D.轻杆对小球B先做正功后做负功
11.如图甲所示,足够长的传送带与水平面夹角为,传送带匀速转动,在传送带上某位置轻轻放置一滑块,滑块质量为m,滑块与传送带间的动摩擦因数为,滑块速度随时间变化的关系如图乙所示,、已知,则( )
A.传送带一定顺时针转动
B.的值可能为
C.传送带的速度大于
D.时刻因摩擦产生的热量为
12.如图所示,用光滑金属丝做成一“U”形轨道架,下边圆弧部分是半径为的半圆环,直轨道部分足够长,将轨道架固定在竖直平面内,两直轨道竖直。在轨道上套有两个质量相等的小环A和B,用一没有弹性的轻杆连接在一起,初始时小环B恰好位于圆弧的左顶端,然后由静止释放,已知轻杆长度为,小环B在最低点时速度为,以下关于两环的运动说法正确的是( )
A.B在圆弧底部时动能最大 B.A下落的最大距离为
C.B在圆弧底部时机械能最大 D.小环B在最低点时A的速度为
13.图中,甲、乙两球质量相同,轻质悬线长度L甲>L乙,悬点等高。先将悬线拉至水平位置,再无初速地释放两球,设甲球通过最低点时的动能为Ek甲,此时悬线的拉力为F甲,甲球的向心加速度为a甲,乙球通过最低点时的动能为Ek乙,此时悬线的拉力为F乙,乙球的向心加速度为a乙,则下列结论中正确的是( )
A.Ek甲>Ek乙
B.F甲>F乙
C.a甲=a乙
D.相对于同一参考平面,甲球到达最低点时的机械能小于乙球到达最低点的机械能
14.如图所示,高的斜面固定不动。一个质量的物体,由静止开始从斜面的顶点滑下,滑到斜面底端时的速度大小为,g取,在此过程中,下列判断正确的是( )
A.系统的机械能保持不变 B.物体的重力势能减少了25J
C.物体的动能增加了18J D.物体的机械能减少了7J
15.如图所示,有两个物块A和,质量分别为和,用同一根轻质细线将两个物块连接在滑轮组上,滑轮质量不计,不计一切摩擦及空气阻力,重力加速度为g,现将两物块由静止释放,经过一段时间,A的位移为,在此过程中,下列说法正确的( )
A.物块A和总势能保持不变 B.A的位移为时,的速度为
C.细线的拉力大小为 D.A和重力的功率大小之比为1:3
二、填空题
16.劲度系数为k的轻弹簧一端固定在墙上,另一端与质量为m的物体相连,物体与桌面间的摩擦因数为μ.初始时刻物体静止,弹簧为自然长度.若向右以恒力F(F>μmg)拉物体,则该物体能够到达的最远位置与初始位置的距离为_____.
17.质量的小球系于弹簧的一端,套在光滑竖直圆环上,弹簧的另一端固定在环上的A点,环半径,弹簧原长。当球从图中位置C滑至最低点B时,测得,则在B点时弹簧的弹性势能______。
18.将一小球竖直向上抛出,若小球的速度越大空气阻力越大,那么,小球在先上升后下降的过程中,它的机械能___________,它受的合力___________。(选填“变大”、“不变”、“变小”)。
19.如图所示,在倾角为30°的斜面上,以3J的动能水平抛出一物体,当这个物体落到斜面上某一点时,它的动能为____________J。
三、综合题
20.如图所示,将倾角θ=30°、表面粗糙的斜面固定在地面上,用一根轻质细绳跨过两个光滑的半径很小的滑轮连接甲、乙两物体(均可视为质点),把甲物体放在斜面上且细绳与斜面平行,把乙物体悬在空中,并使细绳拉直且偏离竖直方向α=60°。开始时甲、乙均静止。现同时释放甲、乙两物体,乙物体将在竖直平面内往返运动,测得绳长OA为l=0.5m,当乙物体运动经过最高点和最低点时,甲物体在斜面上均恰好未滑动,已知乙物体的质量为 m=1kg,忽略空气阻力,取重力加速度g=10m/s2,求:
(1)乙物体在竖直平面内运动到最低点时的速度大小以及所受的拉力大小
(2)甲物体的质量以及斜面对甲物体的最大静摩擦力的大小
(3)斜面与甲物体之间的动摩擦因数μ(设最大静摩擦力等于滑动摩擦力)
21.如图所示,两个半径均为R的光滑圆弧形轨道竖直放置,圆心在同一高度,一倾角为37°的固定光滑斜面与两圆弧轨道相切于C、D(斜面与左侧圆弧轨道的缝隙可以忽略不计),一质量为m的物块(可看成质点)放在光滑水平面的A点,左侧圆弧轨道与水平轨道相切.已知sin37°=0.6,cos37°=0.8.
(1)要使物块能到达E点,则物块在A点的初速度至少多大
(2)若物块在A点的初速度为,求物块从E点抛出后到落到斜面上所用的时间.
22.如图所示,半径的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A。一质量的小球,以初速度在水平地面上向左作匀减速直线运动,球与粗糙水平地面间的动摩擦因数,运动4m后,冲上竖直半圆环,经过最高点B最后小球落在C点。取重力加速度。求:
(1)小球到达A点时速度大小?
(2)小球经过B点时对轨道的压力大小?
(3)A、C两点间的距离?
23.如图所示,质量均为m=0.5 kg的A、B两小物块用轻质弹簧相连,竖直静止放置在水平地面上,弹簧的劲度系数为k=0.5 N/cm,B物块上系一根轻绳,轻绳绕过固定光滑的定滑轮与水平面上的C物块相连,C物块的质量为M=1 kg,与水平面间的动摩擦因数为0.2,初始时轻绳伸直但无拉力。用一水平向右的拉力F作用在C物块上,使C物块向右做匀加速直线运动,1s时A物块恰好离开地面,重力加速度大小g=10 m/s2,求:
(1)A物块刚好离开地面时,水平拉力F的大小;
(2)A物块刚好离开地面前,水平拉力F做功的大小。
试卷第1页,共3页
参考答案:
1.B
【详解】
冰箱消耗电能使冰箱内外发生热交换而达到内部制冷,把冰箱与房间看成一个系统,打开冰箱门后,冰箱与房间内的热交换发生在系统内,系统内部无法使系统总能量发生变化。但系统消耗电能增加了系统的总能量,根据能量守恒定律,系统增加的能量转化为内能使房间的温度升高。
故选B。
2.D
【详解】
A.1s末货物的加速度大小为
选项A错误;
B.根据
P=mgv
可知,前2s内货物克服重力做功的功率不断增加,选项B错误;
C.最后内货物向上减速,加速度向下,处于失重状态,选项C错误;
D.在第4s末至第7s末的过程中,拉力向上做正功,则货物的机械能增大,选项D正确。
故选D。
3.D
【详解】
A.由牛顿第二定律得
mgsin30°+f=m×0.6g
解得摩擦力
f=0.1mg
此过程有摩擦力做功,机械能不守恒,故A错误;
B.物体在斜面上能够上升的最大高度为h,所以重力势能增加了 EP=mgh,故B错误;
C.由动能定理可知,动能损失量为合外力做的功的大小,即
Ek=F合 s=m×0.6g×2h=1.2mgh
故C错误;
D.由功能关系知,机械能的损失量为
E=fs=0.1mg×2h=0.2mgh
故D正确。
故选D。
4.A
【详解】
试题分析:根据功能原理得,物体上升过程中摩擦力做功为:Wf=E2-E1=30J-50J=-20J,在整个过程中由动能定理得:EK-EK0=2Wf则有:EK=EK0+2W=50+2×(-20)=10J,故A正确;物体到达最高点时,机械能为:E=EP=mgh,由图知:EP=30J.得:,故B错误;物体上升过程中,克服摩擦力做功,机械能减少,减少的机械能等于克服摩擦力的功,,即:,得:μ=0.5;物体上升过程中,由牛顿第二定律得:mgsinα+μmgcosα=ma,得:a=gsinα+μgcosα=10×0.6+0.5×10×0.8=10m/s2,故C错误;因为mgsinα>μmgcosα,所以物体不可能静止在斜面顶端.故D错误.故选A.
5.D
【详解】
升降机在从弹簧下端触地后直到最低点的一段运动过程中,开始阶段,重力大于弹力,加速度方向向下,向下做加速运动,当重力和弹力相等后,弹力大于重力,加速度方向向上,向下做减速运动,加速度的大小先减小后增大,速度先增大后减小.故A、B错误.升降机在从弹簧下端触地直到最低点的一段运动过程中,在弹力等于重力之前时,速度在不断增加,则弹力做的负功小于重力所作的正功;在弹力等于重力之后时,速度不断减小,则弹力做的负功大于重力做的正功.故C错误,D正确.故选D.
6.B
【详解】
A.由轨迹图和斜抛运动知识可知,如果足球机械能守恒的话,其轨迹是对称的,由此可知足球在运动过程中受到空气的阻力,故选项A错误;
B.根据
(表示竖直方向的分加速度)
在竖直方向上,足球从1到乙的过程,空气阻力向下
从乙到2的过程空气阻力向上
所以上升过程的时间小于下落过程的时间,故B正确;
C.由于足球受到空气的阻力,故在水平方向的分速度会减小,故足球的起点位置是“1”,故选项C错误;
D.足球在落点的速度小于在起点的速度,根据
可知选项D错误。
故选B。
7.B
【详解】
A.由图2可知,在弹簧恢复原长过程,物块的位移是0.2m,根据
可知做匀加速直线运动的加速度
A错误;
B.初始状态物块处于静止状态有
mg=k△x
加外力瞬间根据牛顿第二定律有
F+k△x-mg=ma
弹簧弹力不能突变,因此有
F=ma
解得
m=2kg
k=100N/m
在弹簧恢复原长瞬间,有
F1-mg=ma
得弹簧恢复原长瞬间弹力
F1=25N
此时刻物块的速度
v=at=1m/s
所以外力F的功率为
P=Fv=25W
B正确;
C.物块和弹簧组成系统的机械能变化量等于外力F做功,在弹簧恢复原长过程中,外力F做功是图2梯形面积,为3J。C错误;
D.在弹簧恢复原长过程中,重力做功
WG=-mgh=-4J
D错误。
故选B。
8.D
【详解】
A.从a到b,弹簧对滑块由沿弹簧向下的拉力,滑块的速度不断增大;从b到c,弹簧对滑块有沿弹簧向上的拉力,开始时拉力沿杆向上的分力小于滑块的重力,滑块仍然在加速,所以滑块在b点时速度不是最大,此时合力为mg,则加速度为g, A错误;
B.从a下滑到c的过程中,对小球和弹簧的系统机械能守恒,由于弹性势能先减小后增加,则小球的机械能先增大后减小, B错误;
C.小球从a点下滑到c点的过程中,由小球和弹簧的系统机械能守恒得
可得滑块在c点的速度大小为
C错误;
D.小球从c点下滑到d点的过程中,小球的机械能减少量等于弹簧弹性势能增加量
解得
D正确。
故选D。
9.B
【详解】
小球在最高点时,速度为0,对杆有压力;设细杆下端被铰链固定,则小球落至水平地面时,细杆中有拉力,由此可知,小球在之前某个时刻就开始对杆有向外的拉力,而本题中细杆下端没有被固定,则小球在这个时刻开始将带着细杆脱离圆周轨道而做斜抛运动,故落地速度斜向右下;由机械能守恒,可知小球落地时的速度大小等于。故ACD错误,B正确。
故选择B。
10.D
【详解】
AB.从A开始下滑到落地的整个过程中,根据功能关系可知,小球A的重力势能转化为AB的动能,对B分析可知,杆对小球B做的功等于B的动能增量,故杆对B做正功;再对A分析可知,A的机械能转移到B上面,故整个过程中杆对A的弹力做负功;故AB错误;
CD.将A球速度分解成沿着杆与垂直于杆方向,同时B球速度也是分解成沿着杆与垂直于杆两方向.
则有,A球:
v⊥=vAsinα
v∥=vAcosα
而B球
v′⊥=vBsinβ
v′∥=vBcosβ
α+β=90°
由于同一杆,则有
vAcosα=vBsinα
则可知,当α达到45°后,B的速度将减小,轻杆做负功;同理轻杆对A做正功;由以上分析可知,轻杆对小球A先做负功再做正功;而轻杆对小球B先做正功再做负功,故C错误,D正确.
故选D.
11.B
【详解】
由图乙所示图象可知,滑块先做初速度为零的匀加速直线运动,在t0后以速度v0做匀速直线运动;由此可知
mgsinθ≤μmgcosθ
如果
mgsinθ>μmgcosθ
滑块在传送带上不会做匀速直线运动;
AC.如果传送带沿逆时针方向转动,滑块放在传送带上后受到的滑动摩擦力沿传送带向下,滑块先做匀加速直线运动,当滑块速度与传送带速度相等时滑块做匀速直线运动,则传送带的速度:v=v0;如果传送带沿顺时针方向转动,滑块刚放在传送带上时受到的滑动摩擦力沿斜面向上,滑块向上做匀加速直线运动,当滑块速度与传送带速度相等时滑块做匀速直线运动,传送带速度:v=v0;传送带速度不会大于v0,传送带即可能沿顺时针也可能沿逆时针方向转动,故AC错误;
B.由图乙所示图象可知,滑块做匀加速直线运动时的加速度
如果传送带沿逆时针方向转动,由牛顿第二定律得
mgsinθ+μmgcosθ=ma
解得
故B正确;
D.在t0时间内物块相对传送带的位移
则摩擦生热
选项D错误。
故选B。
12.B
【详解】
C.根据题意可知,系统机械能守恒,由于杆的长度大于圆弧部分的直径,所以只有环B可以到达轨道右侧,而环A只能在左侧轨道上运动,当杆经过圆弧的圆心位置时,B的机械能最大,A的速度为零,由几何关系可知,选项B正确,C错误;
A.B在最低点右侧某位置重力沿圆弧切线方向的分量与杆的作用力沿圆弧切线方向的分量相等时速度最大,A错误;
D.当环B进入圆弧轨道时两环在沿杆方向的速度分量相同,设B在最低点时A速度为,B的速度为,杆与竖直方向夹角为,如图所示:
有
由几何关系知
又
则A的速度为
选项D错误。
故选B。
13.AC
【详解】
A.根据机械能守恒定律可知
Ek=mgL
可知Ek甲>Ek乙,A正确;
B.根据动能定理得
到达最低点的速度为
在最低点据牛顿第二定律可得
联立解得悬线的拉力为
F=3mg
与悬线长度无关,B错误;
C.结合B的解析可得,向心力加速度为
C正确;
D.相对于同一参考平面,因为两球开始的机械能相同,故甲球到达最低点时的机械能等于乙球到达最低点的机械能,D错误。
故选AC。
14.BCD
【详解】
AD.从顶端到底端,系统的机械能损失
则机械能不守恒,选项A错误,D正确;
B.物体的重力势能减少了
选项B正确;
C.物体的动能增加了
选项C正确;
故选BCD。
15.BC
【详解】
A.根据机械能守恒定律可知,B减小的重力势能全部转化为A的重力势能和两物体的动能,所以,A和B的重力势能之和减小,故A错误;
B.设A上升到h位置时的速度为v1,B的速度为v2,根据动滑轮的特点可知
v2=2v1
根据A和B组成的系统机械能守恒可得
联立解得
故B正确;
C.根据动滑轮的特点可知,A的加速度为B的加速度的一半,根据牛顿第二定律可得,对A有
对B有
又有
a2=2a1
联立解得,轻绳的拉力大小
故C正确;
D.重力功率
由于v2=2v1, ,故A和重力的功率大小之比为1:4,故D错误。
故选BC。
16.
【详解】
设该物体能够到达的最远位置与初始位置的距离为x.根据功能关系得:
Fx=μmgx+
解得:x=(F﹣μmg)
17.15J
【详解】
从C到B过程,据机械能守恒可得
代入数据解得。
18. 变小 变小
【详解】
竖直向上抛出的小球,离开手后会继续向上运动,若考虑空气阻力,小球与空气摩擦,一部分机械能转化为内能,故机械能的总量变小;
小球上升时,受到重力与空气阻力作用,做减速运动,由于二者方向相同,所以合力为二力之和,即
速度减小,阻力减小,则合力减小,到最高点时速度为0,阻力为0,合力为;小球下降时,做加速度运动,由于阻力方向与重力相反,所以合力为二力之差,即
由于小球的速度变大,空气阻力变大,则合力会继续减小,故在整个过程中,小球所受合力越来越小。
19.7
【详解】
设物体的质量为m,初速度为v0,抛出点到落点的高度差为h,水平距离为s,则有
h=stan30°
由平抛运动规律可得
s=v0t
解得
以落点所在平面为参考平面,根据机械能守恒定律得
则
20.(1)2.24 m/s,20 N;(2)2.5 kg,7.5 N;(3)0.35
【详解】
(1)当乙物体运动到最低点时,绳子上的拉力最大,设为F1,对乙物体,由动能定理得
mgl(1-cosα)=
又由牛顿第二定律得
F1-mg=
乙物体在竖直平面内运动到最低点时
v=m/s=2.24m/s?
乙物体运动到最低点时所受的拉力F
F1=20 N
(2)当乙物体运动到最高点时,绳子上的拉力最小,设为F2,此时乙物体向心力为0,即
F2=mgcosα
此时甲物体恰好不下滑,有
Mgsinθ=Ff+F2
乙物体到最低点时,甲物体恰好不上滑,则有
Mgsinθ+Ff=F1
联立解得
M=2.5kg
Ff=7.5 N?
(3)对甲物体,有
Ff=μFN
FN=Mgcosθ
联立解得
μ==0.35
21.(1); (2)
【详解】
解:(1)若斜面是光滑的,物块沿轨道运动过程机械能守恒,设物切到E点时速度为v1,由牛顿第二定律则有
由机械能守恒定律得
在E点有:F≥0
解得
即初速度至少为。
(2)若初速度为,斜面光滑,设物块到E点的速度为,则有
解得
从E点拋出,物块做平抛运动,由平抛运动规律可有
由几何关系有
计算的结果为
22.(1);(2);(3)
【详解】
(1)设小球运动长度到达A点,小球从开始运动到A点过程中,由动能定理得
代入数据解得
(2)从A到B过程小球机械能守恒,由机械能守恒定律得
解得
在B点,由牛顿第二定律得
代入数据解得
由牛顿第三定律可知,小球对轨道的压力
(3)小球离开B点后做平抛运动,竖直方向
水平方向
代入数据联立解得
23.(1) F=12.6 N (2) WF=1.52 J
【详解】
(1)初始时,弹簧的压缩量为
A物块刚好离开地面时,弹簧的伸长量为
从初始位置到A物块刚好离开地面的过程,B物块和C物块的位移均为
C物块做匀加速直线运动,有
A物块刚好离开地面时,弹簧弹力大小为mg,对B物块,有
对C物块,有
代入数据解得
(2)当A物块刚好离开地面时,B、C物块的速度大小均为
初始位置时与A物块刚好离开地面时,弹簧的弹性势能相等,对B、C物块与弹簧组成的系统,由功能关系可得
代入数据解得
答案第1页,共2页
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
