华东师大版七年级下册数学 10.5 图形的全等 课件(共24张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 10.5 图形的全等 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 15:40:28 | ||
图片预览





文档简介
(共24张PPT)
10.5 图形的全等
情境激疑
下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
能够完全重合的两个图形叫做全等图形
华师版第10章 轴对称、平移和旋转
七年级(下)
数
学
10.5 图形的全等
探究发现
仔细观察,领悟实质
观察下面两组图形,它们是不是全等图形?为什么?
探索:
两个图形形状相同,但大小不同;
两个图形面积相同,但形状不同。
它们不能重合,不是全等图形
全等形的特征:能够完全重合
探究发现
仔细观察,领悟实质
探索:
如果两个图形全等,它们的形状与大小一定相同吗?
全等图形的形状与大小都相同
能够完全重合的图形叫做全等图形。
(1)全等图形是指两个或两个以上图形的关系;
(2)图形经过翻折、旋转或平移这三种基本的变换,
前后两个图形都是全等图形;
(3)两个全等图形经过翻折、旋转或平移这三种基本的
变换后一定能够完全重合。
全等图形
温馨提示:
探究发现
仔细观察,领悟实质
做一做
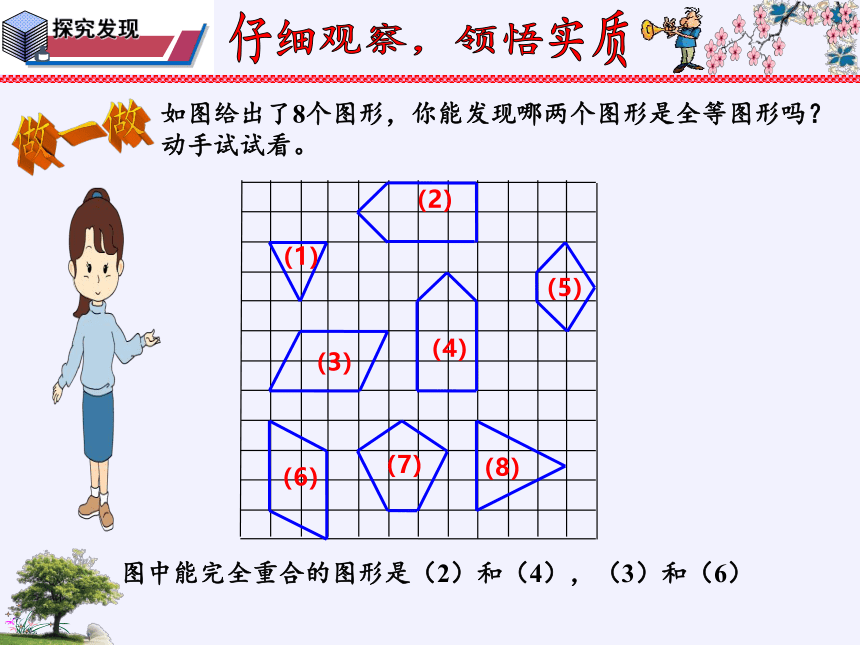
如图给出了8个图形,你能发现哪两个图形是全等图形吗?
动手试试看。
图中能完全重合的图形是(2)和(4),(3)和(6)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
探究发现
仔细观察,领悟实质
探索:
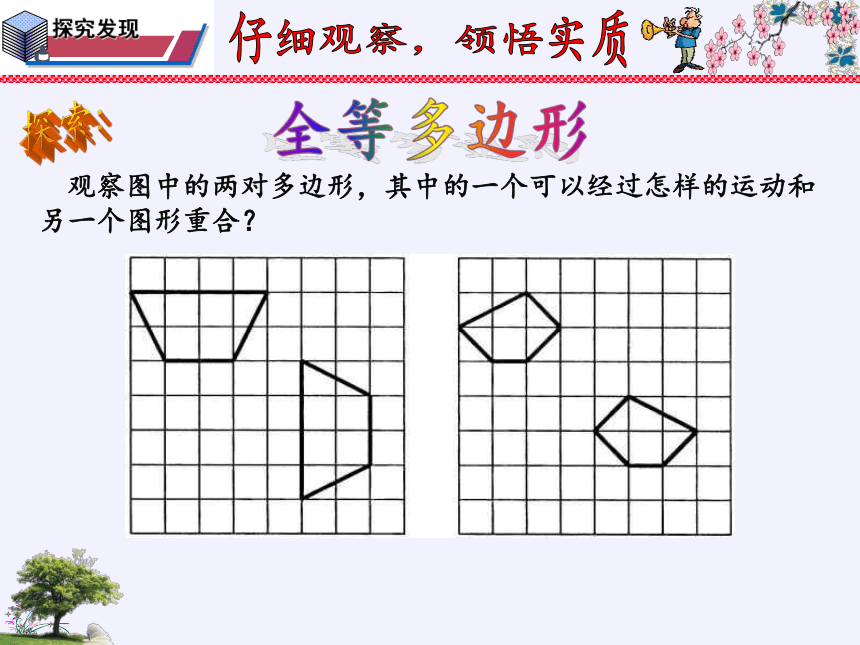
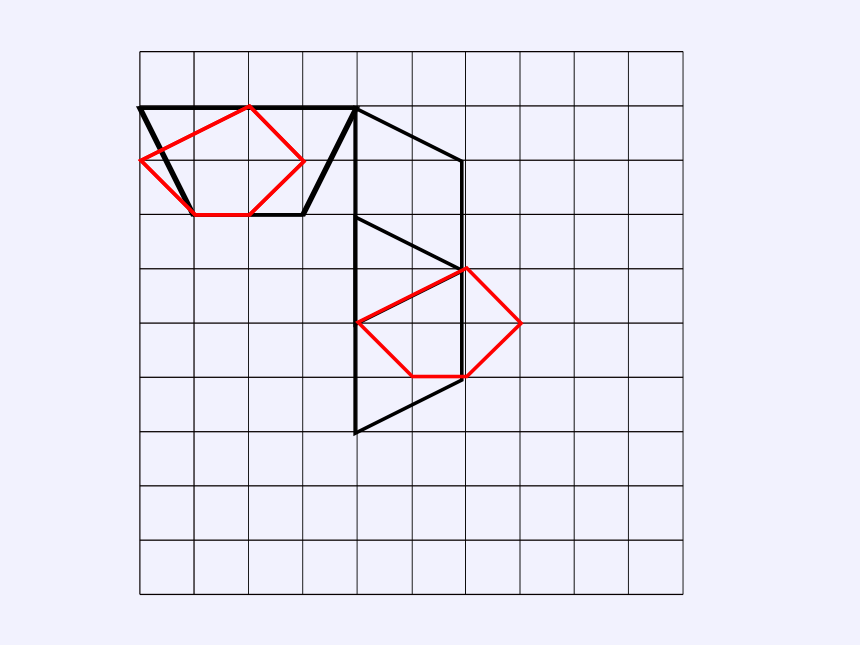
全等多边形
观察图中的两对多边形,其中的一个可以经过怎样的运动和另一个图形重合?
探究发现
仔细观察,领悟实质
结论
全等多边形
A
B
C
D
E
A′
B′
C′
D′
E′
能够完全重合的多边形叫做全等多边形。相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角。
全等的数学符号表示为:“≌” ,读作“全等于”
如图中的两个五边形是全等的,记作:
五边形ABCDE ≌ 五边形A′B′C′D′E′
全等多边形有哪些性质呢?
对应顶点写在对应的位置哟!
探究发现
结论
全等多边形的性质
全等多边形的对应边相等,对应角相等。
反之
边、角分别相等的多边形是全等多边形。
判定
已知△ABC≌△DEF,指出它们的对应边和对应角
解:对应边是:
对应角是:
AC与DF,AB与DE,BC与EF
∠A与∠FDB,∠ABC与∠E,∠C与∠F
练一练
A
B
C
E
D
F
拓展延伸
仔细观察,领悟实质
结论
全等三角形
能够完全重合的三角形叫做全等多边形。相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角。
D
E
F
A
B
C
△ABC 与△DEF全等
记作:△ABC≌△DEF
拓展延伸
仔细观察,领悟实质
结论
全等三角形
D
E
F
A
B
C
性质:全等三角形的对应边相等,对应角相等。
∵△ABC≌△DEF
∴AB=DE,BC=EF,CA=FD
∠A=∠D,∠B=∠E,∠C=∠F
判定:如果两个三角形的边、角分别对应相等,那么这两个三角形全等。
填一填:
⑴△ ≌△
⑵对应边是
⑶对应角是
ABC
DEC
AC与DC,AB与DE,BC与EC。
∠A与∠D、∠B与∠E、
∠ACB与∠DCE
A
D
C
B
E
练一练
探究发现
仔细观察,领悟实质
试一试
如图, △ABC≌△DEF ,且∠A=∠D,∠B=∠E.你能指出它们之间其他的对应顶点、对应角和对应边吗?
A
B
C
D
F
E
如何快速找对应边、对应角呢?
探究发现
仔细观察,领悟实质
探索:
请你找出图中全等三角形的对应边:
A
B
C
D
A
B
C
D
E
F
规律
(1)有公共边的,公共边是对应边;
(2)一对最长的边是对应边,一对最短的边是对应边。
探究发现
仔细观察,领悟实质
探索:
请你找出图中全等三角形的对应角:
C
D
A
B
E
B
D
A
C
O
规律
(1)有公共角的,公共角是对应角;
(2)有对顶角的,对顶角是对应角;
(3)最大角与最大角,最小角与最小角是对应角。
寻找对应边、对应角的方法:
(1)在表达式上找:利用字母的对应位置来确定对应边和对应角。
(2)在图上找:特殊的边和特殊的角。
(3)对应边所对的角是对应角,对应角所对的边是对应边。
学以致用
例 1
如图,△ABC沿着BC的方向平移至△DEF.
(1)∠A=80 ,∠B=60 ,求∠F的度数;
B
C
A
E
F
D
80°
60°
解:由图形平移的特征,可知△ABC与△DEF的形状、大小相同
即△ABC≌△AEC
∴∠D=∠A=80°,∠DEF=∠B=60°
又∵∠D+∠DEF+ ∠F =180°
∴∠F=180°-∠D-∠DEF
=180°-80°-60°=40°
(2)若AB=8,AC=12,EF=15,求△ABC的周长。
AC与DF有怎样的关系?
数 学 活 动 室
经 典 数 学
1.如图(1),△ABC≌△AEC,∠B=30°,∠ACB=85°,求△AEC各角的度数。
B
C
E
A
30°
85°
2.如图(2),已知△ABC沿BC翻折后,得到△DBC.
(1)△ABC和△DBC有什么关系?
(2)若∠ACD=110°,∠A=100°,求∠ABC的度数?
A
B
C
D
100°
110°
图 (1)
图 (2)
学以致用
例 2
如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)试说明:BD=DE+CE;
(2)△ABD 满足什么条件时,BD//CE?
B
C
D
A
E
我的收获是……
这节课我学到了什么?
我还有……的疑惑
畅谈收获
小 结
习题 10.5
P 136
第1、2题
谢 谢
10.5 图形的全等
情境激疑
下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
能够完全重合的两个图形叫做全等图形
华师版第10章 轴对称、平移和旋转
七年级(下)
数
学
10.5 图形的全等
探究发现
仔细观察,领悟实质
观察下面两组图形,它们是不是全等图形?为什么?
探索:
两个图形形状相同,但大小不同;
两个图形面积相同,但形状不同。
它们不能重合,不是全等图形
全等形的特征:能够完全重合
探究发现
仔细观察,领悟实质
探索:
如果两个图形全等,它们的形状与大小一定相同吗?
全等图形的形状与大小都相同
能够完全重合的图形叫做全等图形。
(1)全等图形是指两个或两个以上图形的关系;
(2)图形经过翻折、旋转或平移这三种基本的变换,
前后两个图形都是全等图形;
(3)两个全等图形经过翻折、旋转或平移这三种基本的
变换后一定能够完全重合。
全等图形
温馨提示:
探究发现
仔细观察,领悟实质
做一做
如图给出了8个图形,你能发现哪两个图形是全等图形吗?
动手试试看。
图中能完全重合的图形是(2)和(4),(3)和(6)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
探究发现
仔细观察,领悟实质
探索:
全等多边形
观察图中的两对多边形,其中的一个可以经过怎样的运动和另一个图形重合?
探究发现
仔细观察,领悟实质
结论
全等多边形
A
B
C
D
E
A′
B′
C′
D′
E′
能够完全重合的多边形叫做全等多边形。相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角。
全等的数学符号表示为:“≌” ,读作“全等于”
如图中的两个五边形是全等的,记作:
五边形ABCDE ≌ 五边形A′B′C′D′E′
全等多边形有哪些性质呢?
对应顶点写在对应的位置哟!
探究发现
结论
全等多边形的性质
全等多边形的对应边相等,对应角相等。
反之
边、角分别相等的多边形是全等多边形。
判定
已知△ABC≌△DEF,指出它们的对应边和对应角
解:对应边是:
对应角是:
AC与DF,AB与DE,BC与EF
∠A与∠FDB,∠ABC与∠E,∠C与∠F
练一练
A
B
C
E
D
F
拓展延伸
仔细观察,领悟实质
结论
全等三角形
能够完全重合的三角形叫做全等多边形。相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角。
D
E
F
A
B
C
△ABC 与△DEF全等
记作:△ABC≌△DEF
拓展延伸
仔细观察,领悟实质
结论
全等三角形
D
E
F
A
B
C
性质:全等三角形的对应边相等,对应角相等。
∵△ABC≌△DEF
∴AB=DE,BC=EF,CA=FD
∠A=∠D,∠B=∠E,∠C=∠F
判定:如果两个三角形的边、角分别对应相等,那么这两个三角形全等。
填一填:
⑴△ ≌△
⑵对应边是
⑶对应角是
ABC
DEC
AC与DC,AB与DE,BC与EC。
∠A与∠D、∠B与∠E、
∠ACB与∠DCE
A
D
C
B
E
练一练
探究发现
仔细观察,领悟实质
试一试
如图, △ABC≌△DEF ,且∠A=∠D,∠B=∠E.你能指出它们之间其他的对应顶点、对应角和对应边吗?
A
B
C
D
F
E
如何快速找对应边、对应角呢?
探究发现
仔细观察,领悟实质
探索:
请你找出图中全等三角形的对应边:
A
B
C
D
A
B
C
D
E
F
规律
(1)有公共边的,公共边是对应边;
(2)一对最长的边是对应边,一对最短的边是对应边。
探究发现
仔细观察,领悟实质
探索:
请你找出图中全等三角形的对应角:
C
D
A
B
E
B
D
A
C
O
规律
(1)有公共角的,公共角是对应角;
(2)有对顶角的,对顶角是对应角;
(3)最大角与最大角,最小角与最小角是对应角。
寻找对应边、对应角的方法:
(1)在表达式上找:利用字母的对应位置来确定对应边和对应角。
(2)在图上找:特殊的边和特殊的角。
(3)对应边所对的角是对应角,对应角所对的边是对应边。
学以致用
例 1
如图,△ABC沿着BC的方向平移至△DEF.
(1)∠A=80 ,∠B=60 ,求∠F的度数;
B
C
A
E
F
D
80°
60°
解:由图形平移的特征,可知△ABC与△DEF的形状、大小相同
即△ABC≌△AEC
∴∠D=∠A=80°,∠DEF=∠B=60°
又∵∠D+∠DEF+ ∠F =180°
∴∠F=180°-∠D-∠DEF
=180°-80°-60°=40°
(2)若AB=8,AC=12,EF=15,求△ABC的周长。
AC与DF有怎样的关系?
数 学 活 动 室
经 典 数 学
1.如图(1),△ABC≌△AEC,∠B=30°,∠ACB=85°,求△AEC各角的度数。
B
C
E
A
30°
85°
2.如图(2),已知△ABC沿BC翻折后,得到△DBC.
(1)△ABC和△DBC有什么关系?
(2)若∠ACD=110°,∠A=100°,求∠ABC的度数?
A
B
C
D
100°
110°
图 (1)
图 (2)
学以致用
例 2
如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)试说明:BD=DE+CE;
(2)△ABD 满足什么条件时,BD//CE?
B
C
D
A
E
我的收获是……
这节课我学到了什么?
我还有……的疑惑
畅谈收获
小 结
习题 10.5
P 136
第1、2题
谢 谢
