2021-2022学年高一下学期数学人教A版(2019)必修第二册第九章 统计 单元测试word版含答案
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册第九章 统计 单元测试word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 336.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览



文档简介
统计 单元测试
一、单选题(共12小题,每题5分,共60分)
1.为比较甲、乙两地某月时的气温状况,随机选取该月中的天,将这天中时的气温数据(单位:℃)制成如图所示的茎叶图(十位数字为茎,个位数字为叶). 考虑以下结论:
①甲地该月时的平均气温低于乙地该月时的平均气温;
②甲地该月时的平均气温高于乙地该月时的平均气温;
③甲地该月时的气温的标准差小于乙地该月时的气温的标准差;
④甲地该月时的气温的标准差大于乙地该月时的气温的标准差.
其中根据茎叶图能得到的统计结论的编号为( )
A.①③ B.①④ C.②③ D.②④
2.为了加快新冠病毒检测效率,某检测机构采取“k合1检测法”,即将k个人的拭子样本合并检测,若为阴性,则可以确定所有样本都是阴性的,若为阳性,则还需要对本组的每个人再单独做检测.该检测机构采用了“10合1检测法”对2000人进行检测,检测结果为5人呈阳性,且这5个人来自4个不同的检测组,则总检测的次数是( )
A.210 B.230 C.240 D.250
3.有一组样本数据、、、,由这组数据得到新样本数据、、、,其中,为非零常数,则( )
A.两组样本数据的样本平均数相同 B.两组样本数据的样本标准差相同
C.两组样本数据的样本中位数相同 D.两组样本数据的样本众数相同
4.某学校随机抽取了部分学生,对他们每周使用手机的时间进行统计,得到如下的频率分布直方图.则下列说法:①;②若抽取100人,则平均用时13.75小时;③若从每周使用时间在,,三组内的学生中用分层抽样的方法选取8人进行访谈,则应从使用时间在内的学生中选取的人数为3.其中正确的序号是( )
A.①② B.①③ C.②③ D.①②③
5.为了解某中学对新冠疫情防控知识的宣传情况,增强学生日常防控意识,现从该校随机抽取30名学生参加防控知识测试,得分(10分制)如图所示,以下结论正确的是( )
A.这30名学生测试得分的中位数为6
B.这30名学生测试得分的众数与中位数相等
C.这30名学生测试得分的平均数比中位数小
D.从这30名学生的测试得分可预测该校学生对疫情防控的知识掌握不够,建议学校加强学生疫情防控知识的学习,增强学生日常防控意识
6.某校随机抽取100名学生进行“绿色环保知识”问卷测试.测试结果发现这100名学生的得分都在内,按得分情况分成5组:,,,,,得到如图所示的频率分布直方图.则下列说法错误的是( )
A.这100名学生得分的中位数是72.5
B.这100名学生得分的平均数是72.5
C.这100名学生得分小于70分的有50人
D.这100名学生得分不小于90分的有5人
7.已知某样本的容量为100,平均数为80,方差为95.现发现在收集这些数据时,其中的两个数据记录有误,一个错将90记录为70,另一个错将80记录为100.在对错误的数据进行更正后,重新求得样本的平均数为,方差为,则( )
A., B., C., D.,
8.某中学高一年级有200名学生,高二年级有260名学生,高三年级有340名学生,为了了解该校高中学生完成作业情况,现用分层抽样的方法抽取一个容量为40的样本,则高二年级抽取的人数为( )
A.10 B.13 C.17 D.26
9.某班进行了一次数学测试,全班学生的成绩都落在区间内,其成绩的频率分布直方图如图所示,若该班学生这次数学测试成绩的中位数的估计值为,则的值为( )
A. B. C. D.
10.国家高度重视青少年视力健康问题,指出要“共同呵护好孩子的眼睛,让他们拥有一个光明的末来”.某校为了调查学生的视力健康状况,决定从每班随机抽取5名学生进行调查.若某班有50名学生,将每一学生从01到50编号,从下面所给的随机数表的第2行第4列的数开始,每次从左向右选取两个数字,则选取的第三个号码为( )
随机数表如下:
A.13 B.24 C.33 D.36
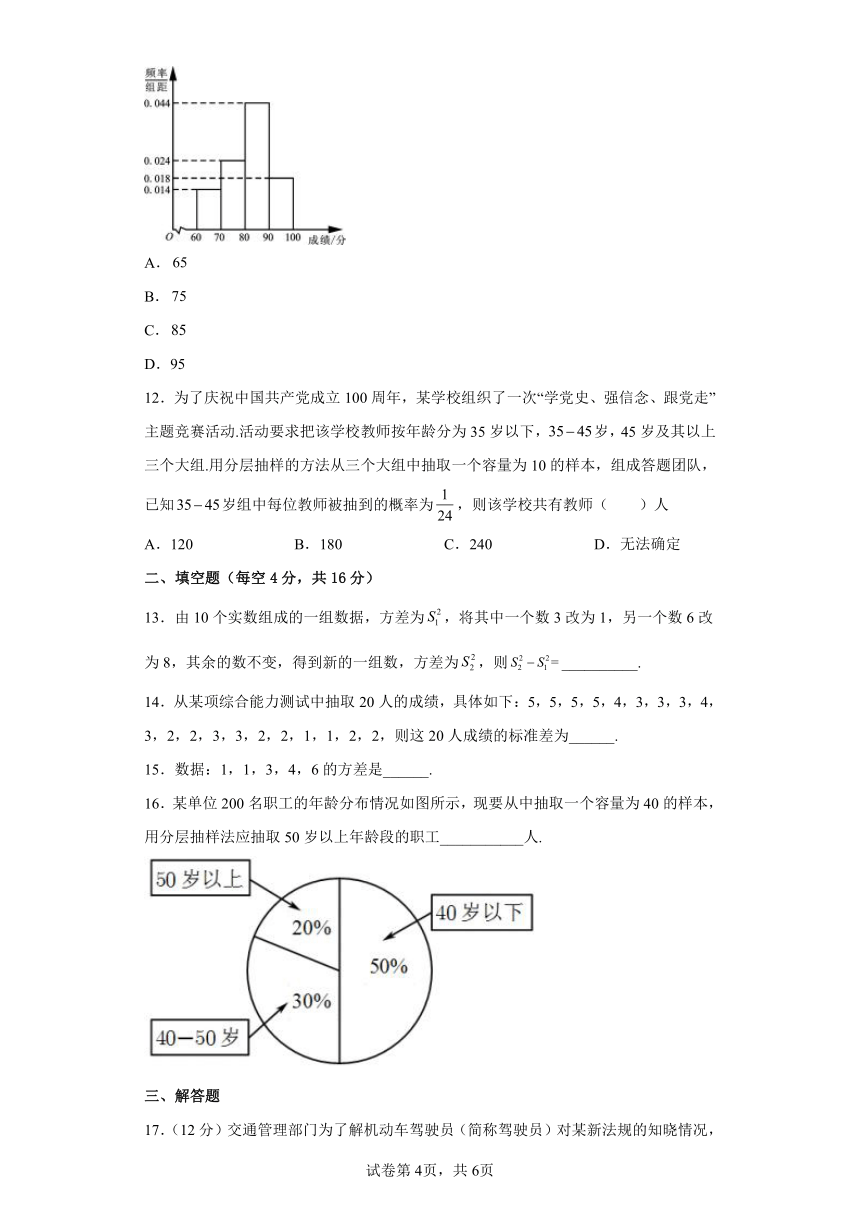
11.为普及冬奥知识,某校在各班选拔部分学生进行冬奥知识竞赛. 根据参赛学生的成绩,得到如图所示的频率分布直方图. 若要对40%成绩较高的学生进行奖励,则获奖学生的最低成绩可能为( )
A.
B.
C.
D.95
12.为了庆祝中国共产党成立100周年,某学校组织了一次“学党史、强信念、跟党走”主题竞赛活动.活动要求把该学校教师按年龄分为35岁以下,岁,45岁及其以上三个大组.用分层抽样的方法从三个大组中抽取一个容量为10的样本,组成答题团队,已知岁组中每位教师被抽到的概率为,则该学校共有教师( )人
A.120 B.180 C.240 D.无法确定
二、填空题(每空4分,共16分)
13.由10个实数组成的一组数据,方差为,将其中一个数3改为1,另一个数6改为8,其余的数不变,得到新的一组数,方差为,则__________.
14.从某项综合能力测试中抽取20人的成绩,具体如下:5,5,5,5,4,3,3,3,4,3,2,2,3,3,2,2,1,1,2,2,则这20人成绩的标准差为______.
15.数据:1,1,3,4,6的方差是______.
16.某单位200名职工的年龄分布情况如图所示,现要从中抽取一个容量为40的样本,用分层抽样法应抽取50岁以上年龄段的职工___________人.
三、解答题
17.(12分)交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查,假设四个社区驾驶员的总人数为,其中甲社区有驾驶员人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为、、、,求丁社区驾驶员的人数.
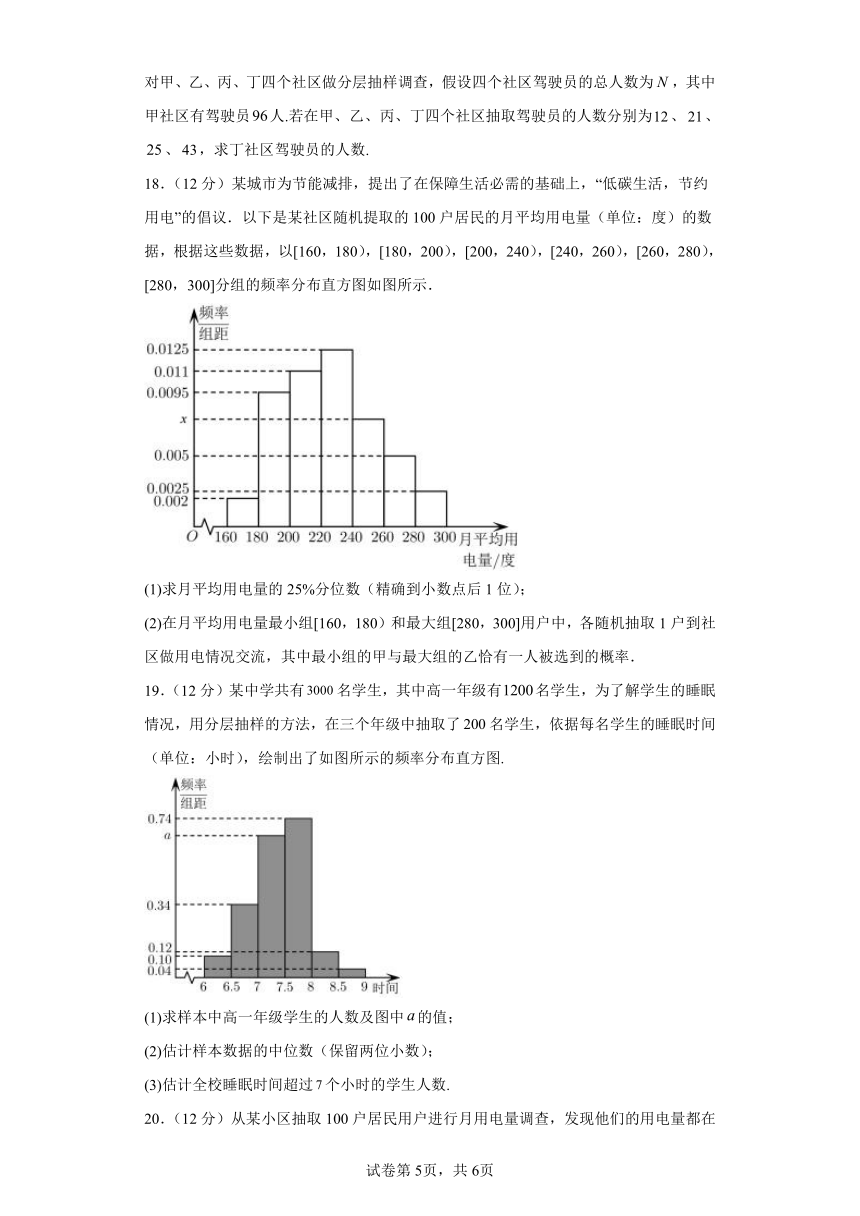
18.(12分)某城市为节能减排,提出了在保障生活必需的基础上,“低碳生活,节约用电”的倡议.以下是某社区随机提取的100户居民的月平均用电量(单位:度)的数据,根据这些数据,以[160,180),[180,200),[200,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.
(1)求月平均用电量的25%分位数(精确到小数点后1位);
(2)在月平均用电量最小组[160,180)和最大组[280,300]用户中,各随机抽取1户到社区做用电情况交流,其中最小组的甲与最大组的乙恰有一人被选到的概率.
19.(12分)某中学共有名学生,其中高一年级有名学生,为了解学生的睡眠情况,用分层抽样的方法,在三个年级中抽取了名学生,依据每名学生的睡眠时间(单位:小时),绘制出了如图所示的频率分布直方图.
(1)求样本中高一年级学生的人数及图中的值;
(2)估计样本数据的中位数(保留两位小数);
(3)估计全校睡眠时间超过个小时的学生人数.
20.(12分)从某小区抽取100户居民用户进行月用电量调查,发现他们的用电量都在50~350(单位:)之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示:
(1)求在被调查的用户中,用电量落在区间的户数;
(2)求直方图中x的值;
(3)求这组数据的平均数.
21.(12分)在考察某高中的学生身高时,采用分层随机抽样的方法,得到了男生身高的平均数为172,女生身高的平均数为162.
(1)如果没有其他信息,怎样估计总体平均数?
(2)如果知道抽取的样本中,男生有20人,女生有15人,怎样估计总体平均数?
22.(14分)为了解某公司新研发的产品在某地区的销售情况,该公司市场营销部在该地区居民中随机选取了人,就他们对该产品的使用情况进行满意度问卷调查,并将他们的满意度评分(满分分)按照分成组,制成如图所示的频率分布直方图.
(1)求图中的值,并求被调查中满意度评分在的人数;
(2)若调查的满意度评分的平均数不低于,则认为该地区居民认可该产品,试判断该地区居民是否认可该产品.(同一组数据用该组数据的中点值作代表)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1-5 BCBBD 6-10 CABAD 11-12CC
13.2
14.
15.
16.
17.
18.(1)201.8
(2)
(1)由图可得月平均用电量在[160,180)的频率为0.002×20=0.04,[180,200)的频率为0.0095×20=0.19,[200,220)的频率为0.011×20=0.22,0.04+0.19=0.23<0.25,0.04+0.19+0.22>0.25,
所以25%分位数一定位于[200,220)内,
由,所以,月平均用电量的25%分位数约为201.8.
(2)
最小组中有4户,设为甲,
最大组有5户,设为乙,,
各随机抽取1户,有(甲,),(甲,),(甲,),(甲,),(甲,乙),
(,乙),(),(),(),(),
(,乙),(),(),(),(),
(,乙),(),(),(),(),
共20种可能,
其中最小组的甲与最大组的乙恰有一人被选到有:(甲,),(甲,),(甲,),(甲,),(,乙),(,乙),(,乙),共7种
甲、乙被选到的事件分别记为A、B,
所以最小组的甲与最大组的乙恰有一人被选到的概率为:.
19.(1)样本中高一年级学生的人数为,;
(2);
(3).
(1)
解:样本中高一年级学生的人数为.
,解得.
(2)
解:设中位数为,前两个矩形的面积之和为,
前三个矩形的面积之和为,所以,
则,得,
故样本数据的中位数约为.
(3)
解:由图可知,样本数据落在的频率为,
故全校睡眠时间超过个小时的学生人数约为.
20.(1)30户
(2)0.0044
(3)
(1)
解:,
所以在被调查的用户中,用电量落在区间的户数为30户
(2)
解:
所以直方图中x的值为0.0044.
(3)
解:各区间的中点值分别为:75 125 175 225 275 325,
所以这组数据的平均数为.
21.(1)估计总体平均数为,详解见解析;
(2)估计总体平均数为,详解见解析
【解析】
(1)
作为估计来说,我们可以选择男生(或女生)样本的平均数作为总体对应值的估计,但这样的选择没有充分利用已有的数据,显然不够好,另外一种估计的方法是取每一层样本平均数作为总体的估计,即估计总体平均数为.
(2)
由加权平均数公式代入,得样本的平均数为,因此估计总体平均数为.
22.(1);300
(2)该地区居民认可该产品
(1)
由,解得.
因为,所以被调查者中满意度评分在的人数为.
(2)
由图可知,调查的满意度评分的平均数.
因为,所以该地区居民认可该产品.答案第1页,共2页
答案第1页,共2页
一、单选题(共12小题,每题5分,共60分)
1.为比较甲、乙两地某月时的气温状况,随机选取该月中的天,将这天中时的气温数据(单位:℃)制成如图所示的茎叶图(十位数字为茎,个位数字为叶). 考虑以下结论:
①甲地该月时的平均气温低于乙地该月时的平均气温;
②甲地该月时的平均气温高于乙地该月时的平均气温;
③甲地该月时的气温的标准差小于乙地该月时的气温的标准差;
④甲地该月时的气温的标准差大于乙地该月时的气温的标准差.
其中根据茎叶图能得到的统计结论的编号为( )
A.①③ B.①④ C.②③ D.②④
2.为了加快新冠病毒检测效率,某检测机构采取“k合1检测法”,即将k个人的拭子样本合并检测,若为阴性,则可以确定所有样本都是阴性的,若为阳性,则还需要对本组的每个人再单独做检测.该检测机构采用了“10合1检测法”对2000人进行检测,检测结果为5人呈阳性,且这5个人来自4个不同的检测组,则总检测的次数是( )
A.210 B.230 C.240 D.250
3.有一组样本数据、、、,由这组数据得到新样本数据、、、,其中,为非零常数,则( )
A.两组样本数据的样本平均数相同 B.两组样本数据的样本标准差相同
C.两组样本数据的样本中位数相同 D.两组样本数据的样本众数相同
4.某学校随机抽取了部分学生,对他们每周使用手机的时间进行统计,得到如下的频率分布直方图.则下列说法:①;②若抽取100人,则平均用时13.75小时;③若从每周使用时间在,,三组内的学生中用分层抽样的方法选取8人进行访谈,则应从使用时间在内的学生中选取的人数为3.其中正确的序号是( )
A.①② B.①③ C.②③ D.①②③
5.为了解某中学对新冠疫情防控知识的宣传情况,增强学生日常防控意识,现从该校随机抽取30名学生参加防控知识测试,得分(10分制)如图所示,以下结论正确的是( )
A.这30名学生测试得分的中位数为6
B.这30名学生测试得分的众数与中位数相等
C.这30名学生测试得分的平均数比中位数小
D.从这30名学生的测试得分可预测该校学生对疫情防控的知识掌握不够,建议学校加强学生疫情防控知识的学习,增强学生日常防控意识
6.某校随机抽取100名学生进行“绿色环保知识”问卷测试.测试结果发现这100名学生的得分都在内,按得分情况分成5组:,,,,,得到如图所示的频率分布直方图.则下列说法错误的是( )
A.这100名学生得分的中位数是72.5
B.这100名学生得分的平均数是72.5
C.这100名学生得分小于70分的有50人
D.这100名学生得分不小于90分的有5人
7.已知某样本的容量为100,平均数为80,方差为95.现发现在收集这些数据时,其中的两个数据记录有误,一个错将90记录为70,另一个错将80记录为100.在对错误的数据进行更正后,重新求得样本的平均数为,方差为,则( )
A., B., C., D.,
8.某中学高一年级有200名学生,高二年级有260名学生,高三年级有340名学生,为了了解该校高中学生完成作业情况,现用分层抽样的方法抽取一个容量为40的样本,则高二年级抽取的人数为( )
A.10 B.13 C.17 D.26
9.某班进行了一次数学测试,全班学生的成绩都落在区间内,其成绩的频率分布直方图如图所示,若该班学生这次数学测试成绩的中位数的估计值为,则的值为( )
A. B. C. D.
10.国家高度重视青少年视力健康问题,指出要“共同呵护好孩子的眼睛,让他们拥有一个光明的末来”.某校为了调查学生的视力健康状况,决定从每班随机抽取5名学生进行调查.若某班有50名学生,将每一学生从01到50编号,从下面所给的随机数表的第2行第4列的数开始,每次从左向右选取两个数字,则选取的第三个号码为( )
随机数表如下:
A.13 B.24 C.33 D.36
11.为普及冬奥知识,某校在各班选拔部分学生进行冬奥知识竞赛. 根据参赛学生的成绩,得到如图所示的频率分布直方图. 若要对40%成绩较高的学生进行奖励,则获奖学生的最低成绩可能为( )
A.
B.
C.
D.95
12.为了庆祝中国共产党成立100周年,某学校组织了一次“学党史、强信念、跟党走”主题竞赛活动.活动要求把该学校教师按年龄分为35岁以下,岁,45岁及其以上三个大组.用分层抽样的方法从三个大组中抽取一个容量为10的样本,组成答题团队,已知岁组中每位教师被抽到的概率为,则该学校共有教师( )人
A.120 B.180 C.240 D.无法确定
二、填空题(每空4分,共16分)
13.由10个实数组成的一组数据,方差为,将其中一个数3改为1,另一个数6改为8,其余的数不变,得到新的一组数,方差为,则__________.
14.从某项综合能力测试中抽取20人的成绩,具体如下:5,5,5,5,4,3,3,3,4,3,2,2,3,3,2,2,1,1,2,2,则这20人成绩的标准差为______.
15.数据:1,1,3,4,6的方差是______.
16.某单位200名职工的年龄分布情况如图所示,现要从中抽取一个容量为40的样本,用分层抽样法应抽取50岁以上年龄段的职工___________人.
三、解答题
17.(12分)交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查,假设四个社区驾驶员的总人数为,其中甲社区有驾驶员人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为、、、,求丁社区驾驶员的人数.
18.(12分)某城市为节能减排,提出了在保障生活必需的基础上,“低碳生活,节约用电”的倡议.以下是某社区随机提取的100户居民的月平均用电量(单位:度)的数据,根据这些数据,以[160,180),[180,200),[200,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.
(1)求月平均用电量的25%分位数(精确到小数点后1位);
(2)在月平均用电量最小组[160,180)和最大组[280,300]用户中,各随机抽取1户到社区做用电情况交流,其中最小组的甲与最大组的乙恰有一人被选到的概率.
19.(12分)某中学共有名学生,其中高一年级有名学生,为了解学生的睡眠情况,用分层抽样的方法,在三个年级中抽取了名学生,依据每名学生的睡眠时间(单位:小时),绘制出了如图所示的频率分布直方图.
(1)求样本中高一年级学生的人数及图中的值;
(2)估计样本数据的中位数(保留两位小数);
(3)估计全校睡眠时间超过个小时的学生人数.
20.(12分)从某小区抽取100户居民用户进行月用电量调查,发现他们的用电量都在50~350(单位:)之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示:
(1)求在被调查的用户中,用电量落在区间的户数;
(2)求直方图中x的值;
(3)求这组数据的平均数.
21.(12分)在考察某高中的学生身高时,采用分层随机抽样的方法,得到了男生身高的平均数为172,女生身高的平均数为162.
(1)如果没有其他信息,怎样估计总体平均数?
(2)如果知道抽取的样本中,男生有20人,女生有15人,怎样估计总体平均数?
22.(14分)为了解某公司新研发的产品在某地区的销售情况,该公司市场营销部在该地区居民中随机选取了人,就他们对该产品的使用情况进行满意度问卷调查,并将他们的满意度评分(满分分)按照分成组,制成如图所示的频率分布直方图.
(1)求图中的值,并求被调查中满意度评分在的人数;
(2)若调查的满意度评分的平均数不低于,则认为该地区居民认可该产品,试判断该地区居民是否认可该产品.(同一组数据用该组数据的中点值作代表)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1-5 BCBBD 6-10 CABAD 11-12CC
13.2
14.
15.
16.
17.
18.(1)201.8
(2)
(1)由图可得月平均用电量在[160,180)的频率为0.002×20=0.04,[180,200)的频率为0.0095×20=0.19,[200,220)的频率为0.011×20=0.22,0.04+0.19=0.23<0.25,0.04+0.19+0.22>0.25,
所以25%分位数一定位于[200,220)内,
由,所以,月平均用电量的25%分位数约为201.8.
(2)
最小组中有4户,设为甲,
最大组有5户,设为乙,,
各随机抽取1户,有(甲,),(甲,),(甲,),(甲,),(甲,乙),
(,乙),(),(),(),(),
(,乙),(),(),(),(),
(,乙),(),(),(),(),
共20种可能,
其中最小组的甲与最大组的乙恰有一人被选到有:(甲,),(甲,),(甲,),(甲,),(,乙),(,乙),(,乙),共7种
甲、乙被选到的事件分别记为A、B,
所以最小组的甲与最大组的乙恰有一人被选到的概率为:.
19.(1)样本中高一年级学生的人数为,;
(2);
(3).
(1)
解:样本中高一年级学生的人数为.
,解得.
(2)
解:设中位数为,前两个矩形的面积之和为,
前三个矩形的面积之和为,所以,
则,得,
故样本数据的中位数约为.
(3)
解:由图可知,样本数据落在的频率为,
故全校睡眠时间超过个小时的学生人数约为.
20.(1)30户
(2)0.0044
(3)
(1)
解:,
所以在被调查的用户中,用电量落在区间的户数为30户
(2)
解:
所以直方图中x的值为0.0044.
(3)
解:各区间的中点值分别为:75 125 175 225 275 325,
所以这组数据的平均数为.
21.(1)估计总体平均数为,详解见解析;
(2)估计总体平均数为,详解见解析
【解析】
(1)
作为估计来说,我们可以选择男生(或女生)样本的平均数作为总体对应值的估计,但这样的选择没有充分利用已有的数据,显然不够好,另外一种估计的方法是取每一层样本平均数作为总体的估计,即估计总体平均数为.
(2)
由加权平均数公式代入,得样本的平均数为,因此估计总体平均数为.
22.(1);300
(2)该地区居民认可该产品
(1)
由,解得.
因为,所以被调查者中满意度评分在的人数为.
(2)
由图可知,调查的满意度评分的平均数.
因为,所以该地区居民认可该产品.答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
