四川省南充市蓬安县2021-2022学年七年级下学期开学考试数学试题(word版,无答案)
文档属性
| 名称 | 四川省南充市蓬安县2021-2022学年七年级下学期开学考试数学试题(word版,无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 62.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 16:10:13 | ||
图片预览

文档简介
2021—2022学年七年级下学期开学考试试题
数 学
考试时间120分钟,试卷满分150分
一、选择题(每题4分,共40分)
1.如果收入50元,记作+50元,那么支出30元记作( )
A.+30元 B.-30元 C.+80元 D.-80元
2.下列说法错误的是( )
A.有数字与字母的乘积组成的代数式叫做单项式。
B.几个单项式的和叫做多项式。
C.单项式与多项式统称整式。
D.一个数字不是一个单项式,它的次数是0。
3.我国在2020年10月开展了第七次人口普查,普查数据显示,我国2020年总人口达到14.1亿,将14.1亿用科学记数法表示为( )
A.14.1×107 B.14.1×108 C.1.41×109 D.1.41×1010
4.化简(9x﹣3)﹣2(x+1)的结果是( )
A.2x﹣2 B.x+1 C.5x+3 D.x﹣3
5.下列运用等式的性质,变形正确的是( )
A.若x=y,则x﹣5=y+5 B.若a=b,则ac=bc
C.若,则2a=3b D.若x=y,则
6.下列几何体是由4个相同的小正方体搭成的,其中左视图和俯视图相同的是( )
A. B. C. D.
7.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值等于( )
A.45° B.60° C.90° D.180°
8.如图,C是线段AB上一点,M是线段AC的中点,若AB=8cm,BC=2cm,则MC的长是( )
A.2cm B.3cm C.4cm D.6cm
9.南充市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
A.5(x+21-1)=6(x-1) B.5(x+21)=6(x-1)
C.5(x+21-1)=6x D.5(x+21)=6x
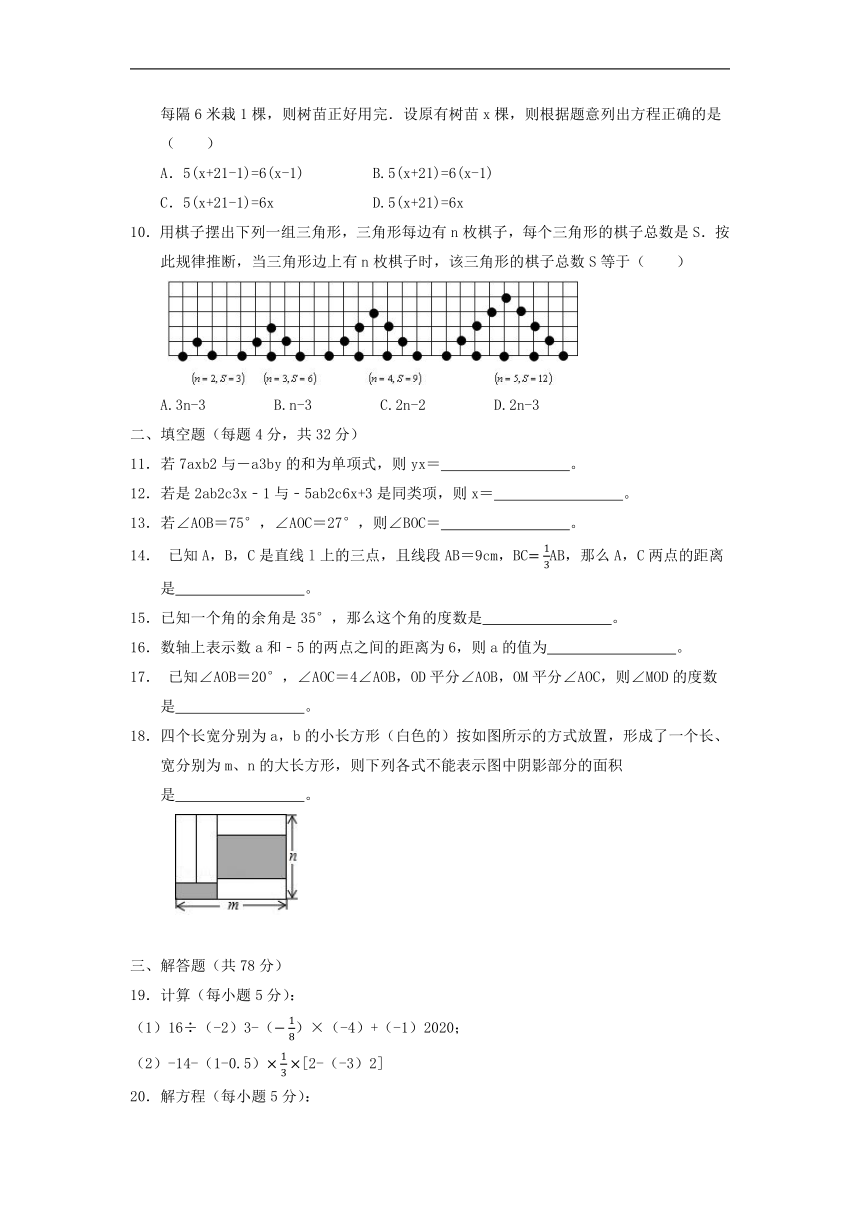
10.用棋子摆出下列一组三角形,三角形每边有n枚棋子,每个三角形的棋子总数是S.按此规律推断,当三角形边上有n枚棋子时,该三角形的棋子总数S等于( )
A.3n-3 B.n-3 C.2n-2 D.2n-3
二、填空题(每题4分,共32分)
11.若7axb2与-a3by的和为单项式,则yx= 。
12.若是2ab2c3x﹣1与﹣5ab2c6x+3是同类项,则x= 。
13.若∠AOB=75°,∠AOC=27°,则∠BOC= 。
14. 已知A,B,C是直线l上的三点,且线段AB=9cm,BCAB,那么A,C两点的距离是 。
15.已知一个角的余角是35°,那么这个角的度数是 。
16.数轴上表示数a和﹣5的两点之间的距离为6,则a的值为 。
17. 已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是 。
18.四个长宽分别为a,b的小长方形(白色的)按如图所示的方式放置,形成了一个长、宽分别为m、n的大长方形,则下列各式不能表示图中阴影部分的面积是 。
三、解答题(共78分)
19.计算(每小题5分):
(1)16÷(-2)3-()×(-4)+(-1)2020;
(2)-14-(1-0.5)[2-(-3)2]
20.解方程(每小题5分):
(1)-4x-2(1-x)=7+5x; (2)1.
21.(10分)先化简,再求值:
3(2x2-3xy-5x-1)+6(-x2+xy-1),其中x、y满足(x+2)2+|y|=0
22.(12分)尺规作图:
如图,已知线段a,b,c.
(1)求作一条线段,使它等于a+2b;
(2)求作一条线段,使它等于a﹣b+c.
要求:保留作图痕迹,写出结论,但不要求写出作法.
23.(12分)如图,已知线段AD=30cm,点C、B都是线段AD上的点,点E是AB的中点.
(1)若BD=6cm,求线段AE的长;
(2)在(1)的条件下,若ACAD,且点F是线段CD的中点,求线段EF的长.
24.(12分)某班计划买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价100元,乒乓球每盒定价25元.经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不少于5盒).问:
(1)当购买乒乓球多少盒时,两种优惠办法付款一样?
(2)当购买20盒、40盒乒乓球时,去哪家商店购买更合算?
25.(12分)如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠D=30°)的直角顶点放在点O处,一边OE在射线OA上,另一边OD与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒5°的速度沿顺时针方向旋转一周,如图2,经过t秒后,OD恰好平分∠BOC.
①此时t的值为 ;(直接填空)
②此时OE是否平分∠AOC?请说明理由;
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒8°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠DOE?请说明理由;
(3)在(2)问的基础上,经过多长时间OC平分∠DOB?请画图并说明理由.
数 学
考试时间120分钟,试卷满分150分
一、选择题(每题4分,共40分)
1.如果收入50元,记作+50元,那么支出30元记作( )
A.+30元 B.-30元 C.+80元 D.-80元
2.下列说法错误的是( )
A.有数字与字母的乘积组成的代数式叫做单项式。
B.几个单项式的和叫做多项式。
C.单项式与多项式统称整式。
D.一个数字不是一个单项式,它的次数是0。
3.我国在2020年10月开展了第七次人口普查,普查数据显示,我国2020年总人口达到14.1亿,将14.1亿用科学记数法表示为( )
A.14.1×107 B.14.1×108 C.1.41×109 D.1.41×1010
4.化简(9x﹣3)﹣2(x+1)的结果是( )
A.2x﹣2 B.x+1 C.5x+3 D.x﹣3
5.下列运用等式的性质,变形正确的是( )
A.若x=y,则x﹣5=y+5 B.若a=b,则ac=bc
C.若,则2a=3b D.若x=y,则
6.下列几何体是由4个相同的小正方体搭成的,其中左视图和俯视图相同的是( )
A. B. C. D.
7.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值等于( )
A.45° B.60° C.90° D.180°
8.如图,C是线段AB上一点,M是线段AC的中点,若AB=8cm,BC=2cm,则MC的长是( )
A.2cm B.3cm C.4cm D.6cm
9.南充市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
A.5(x+21-1)=6(x-1) B.5(x+21)=6(x-1)
C.5(x+21-1)=6x D.5(x+21)=6x
10.用棋子摆出下列一组三角形,三角形每边有n枚棋子,每个三角形的棋子总数是S.按此规律推断,当三角形边上有n枚棋子时,该三角形的棋子总数S等于( )
A.3n-3 B.n-3 C.2n-2 D.2n-3
二、填空题(每题4分,共32分)
11.若7axb2与-a3by的和为单项式,则yx= 。
12.若是2ab2c3x﹣1与﹣5ab2c6x+3是同类项,则x= 。
13.若∠AOB=75°,∠AOC=27°,则∠BOC= 。
14. 已知A,B,C是直线l上的三点,且线段AB=9cm,BCAB,那么A,C两点的距离是 。
15.已知一个角的余角是35°,那么这个角的度数是 。
16.数轴上表示数a和﹣5的两点之间的距离为6,则a的值为 。
17. 已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是 。
18.四个长宽分别为a,b的小长方形(白色的)按如图所示的方式放置,形成了一个长、宽分别为m、n的大长方形,则下列各式不能表示图中阴影部分的面积是 。
三、解答题(共78分)
19.计算(每小题5分):
(1)16÷(-2)3-()×(-4)+(-1)2020;
(2)-14-(1-0.5)[2-(-3)2]
20.解方程(每小题5分):
(1)-4x-2(1-x)=7+5x; (2)1.
21.(10分)先化简,再求值:
3(2x2-3xy-5x-1)+6(-x2+xy-1),其中x、y满足(x+2)2+|y|=0
22.(12分)尺规作图:
如图,已知线段a,b,c.
(1)求作一条线段,使它等于a+2b;
(2)求作一条线段,使它等于a﹣b+c.
要求:保留作图痕迹,写出结论,但不要求写出作法.
23.(12分)如图,已知线段AD=30cm,点C、B都是线段AD上的点,点E是AB的中点.
(1)若BD=6cm,求线段AE的长;
(2)在(1)的条件下,若ACAD,且点F是线段CD的中点,求线段EF的长.
24.(12分)某班计划买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价100元,乒乓球每盒定价25元.经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不少于5盒).问:
(1)当购买乒乓球多少盒时,两种优惠办法付款一样?
(2)当购买20盒、40盒乒乓球时,去哪家商店购买更合算?
25.(12分)如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠D=30°)的直角顶点放在点O处,一边OE在射线OA上,另一边OD与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒5°的速度沿顺时针方向旋转一周,如图2,经过t秒后,OD恰好平分∠BOC.
①此时t的值为 ;(直接填空)
②此时OE是否平分∠AOC?请说明理由;
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒8°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠DOE?请说明理由;
(3)在(2)问的基础上,经过多长时间OC平分∠DOB?请画图并说明理由.
同课章节目录
