【分层教学方案】第04课时 矩形的性质 课件
文档属性
| 名称 | 【分层教学方案】第04课时 矩形的性质 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 00:00:00 | ||
图片预览







文档简介
(共43张PPT)
课时分层教学方案探究
第04课时
矩形的性质
九年级上学期
一、学习目标
二、知识准备
三、新课学习
知识点1
知识点2
例题1
反馈1
例题2
反馈2
四、课堂练习
A1
A2
A3
/
A4
A5
A6
A7
A8
A9
五、知识梳理
可
可
O
O
O
6
00
柚学
Yoo Sehool
专业打造深圳教辅本土品牌
柚学智能图书
Book.
WWWWW.
0
课时分层
教学方案探究
20+b=X
唐云军
编
+400+40X20=0
x ut cos (a)
y=ut sin (a)-1/2 gt
va.-
va
V04/2
Vb=1/2u1
数学
部分
vb'+VC'=vb
1-eA2
vb'-vc'=-ev
九年级上
1+e)2
Vb=1/4u(1-e2)
Vb'=1/4u1-e^
1/4u1+eA2
vc'=1/4u(1+e)A2
314150.654
Ra+400+40X2a=0
知识点1
柚学
选题》
知识点1
知识点2
知识点3
返回新课学习
知识点1
矩形的性质
柚学
【读一读】
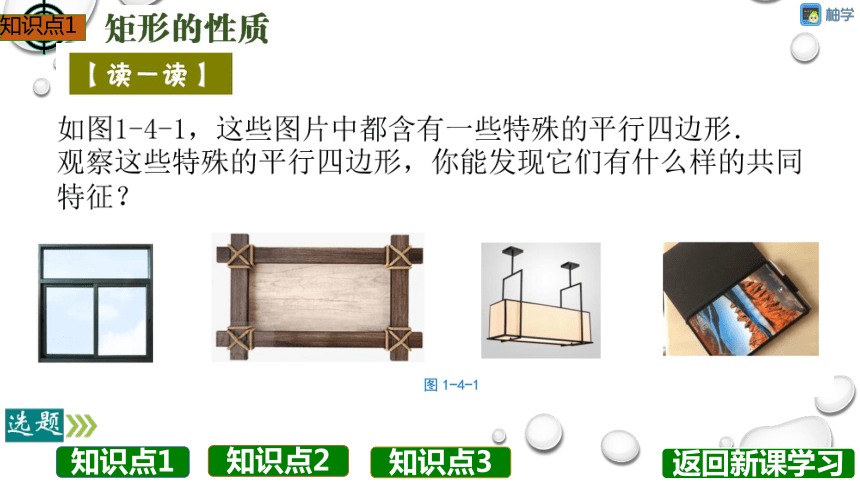
如图1-4-1,这些图片中都含有一些特殊的平行四边形.
观察这些特殊的平行四边形,你能发现它们有什么样的共同
特征?
图1-4-1
选题》
知识点1
知识点2
知识点3
返回新课学习
如图1-4-1,这些图片中都含有一些特殊的平行四边形
观察这些特殊的平行四边形,你能发现它们有什么样的共同
特征?
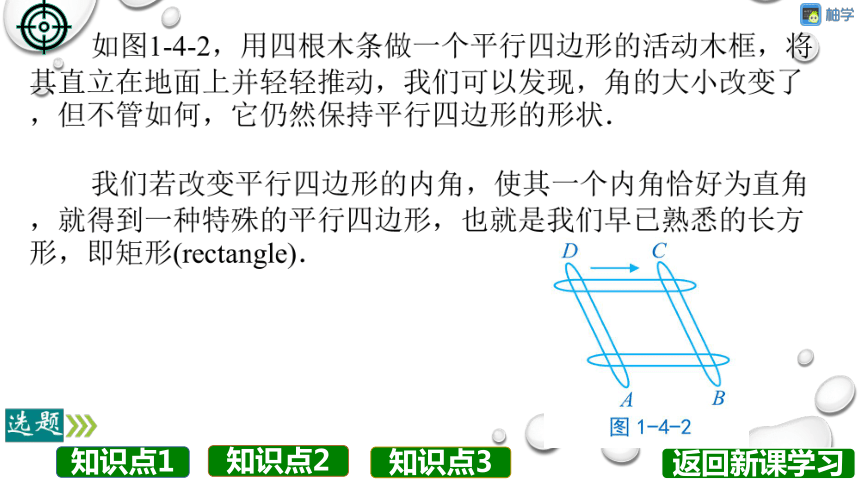
如图1-4-2,用四根木条做一个平行四边形的活动木框,将
其直立在地面上并轻轻推动,我们可以发现,角的大小改变了
但不管如何,它仍然保持平行四边形的形状
我们若改变平行四边形的内角,使其一个内角恰好为直角
就得到一种特殊的平行四边形,也就是我们早已熟悉的长方
形,即矩形(rectangle).
答:对边平行且相等:对角相等
对角线相互平分;是中心对称图形.
通过观察,可以发现
矩形的四个角都是直角
②对角线相等
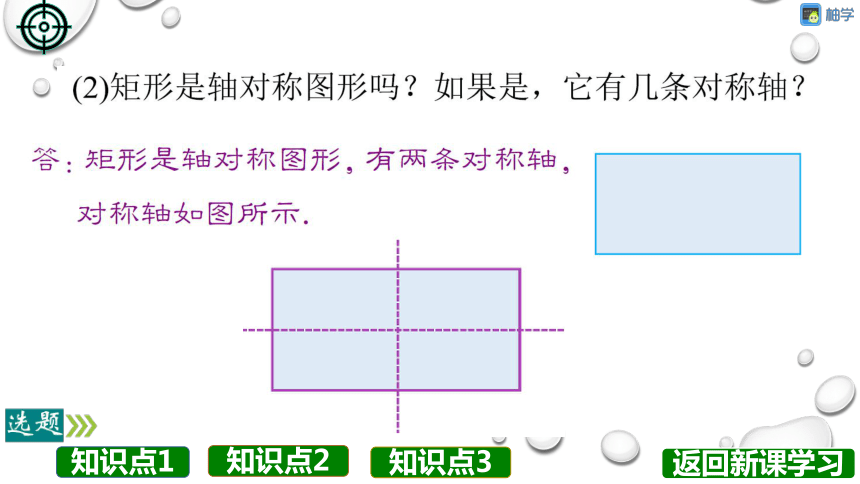
③是轴对称图形
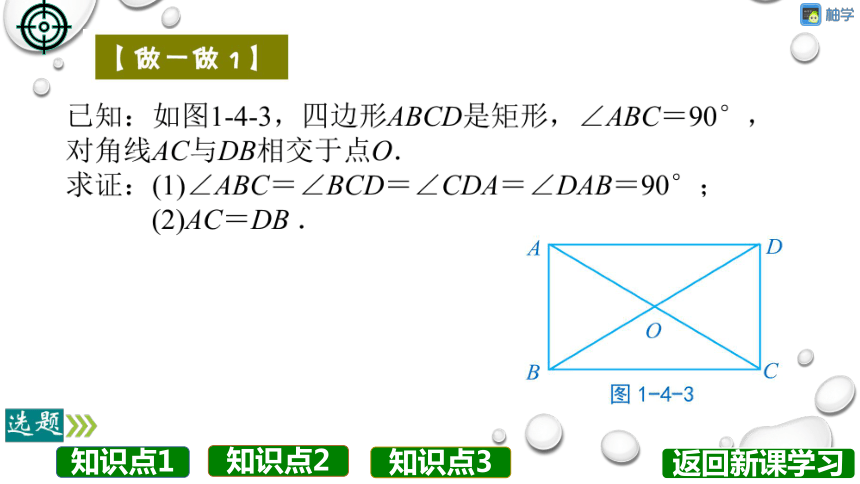
已知:如图1-4-3,四边形ABCD是矩形,∠ABC=90°,
对角线AC与DB相交于点O.
求证:(1)∠ABC=∠BCD=∠CDA=∠DAB=90
(2AC-DB
证明:(1).四边形ABCD是矩形
.∠ABC=∠CDA,∠BCD=∠DAB(矩形的对角相等)
,'AB升DC(矩形的对边平元)
∠ABC
∠BCD=180°
又,∠ABC
∠CDA=∠DAB=90
课时分层教学方案探究
第04课时
矩形的性质
九年级上学期
一、学习目标
二、知识准备
三、新课学习
知识点1
知识点2
例题1
反馈1
例题2
反馈2
四、课堂练习
A1
A2
A3
/
A4
A5
A6
A7
A8
A9
五、知识梳理
可
可
O
O
O
6
00
柚学
Yoo Sehool
专业打造深圳教辅本土品牌
柚学智能图书
Book.
WWWWW.
0
课时分层
教学方案探究
20+b=X
唐云军
编
+400+40X20=0
x ut cos (a)
y=ut sin (a)-1/2 gt
va.-
va
V04/2
Vb=1/2u1
数学
部分
vb'+VC'=vb
1-eA2
vb'-vc'=-ev
九年级上
1+e)2
Vb=1/4u(1-e2)
Vb'=1/4u1-e^
1/4u1+eA2
vc'=1/4u(1+e)A2
314150.654
Ra+400+40X2a=0
知识点1
柚学
选题》
知识点1
知识点2
知识点3
返回新课学习
知识点1
矩形的性质
柚学
【读一读】
如图1-4-1,这些图片中都含有一些特殊的平行四边形.
观察这些特殊的平行四边形,你能发现它们有什么样的共同
特征?
图1-4-1
选题》
知识点1
知识点2
知识点3
返回新课学习
如图1-4-1,这些图片中都含有一些特殊的平行四边形
观察这些特殊的平行四边形,你能发现它们有什么样的共同
特征?
如图1-4-2,用四根木条做一个平行四边形的活动木框,将
其直立在地面上并轻轻推动,我们可以发现,角的大小改变了
但不管如何,它仍然保持平行四边形的形状
我们若改变平行四边形的内角,使其一个内角恰好为直角
就得到一种特殊的平行四边形,也就是我们早已熟悉的长方
形,即矩形(rectangle).
答:对边平行且相等:对角相等
对角线相互平分;是中心对称图形.
通过观察,可以发现
矩形的四个角都是直角
②对角线相等
③是轴对称图形
已知:如图1-4-3,四边形ABCD是矩形,∠ABC=90°,
对角线AC与DB相交于点O.
求证:(1)∠ABC=∠BCD=∠CDA=∠DAB=90
(2AC-DB
证明:(1).四边形ABCD是矩形
.∠ABC=∠CDA,∠BCD=∠DAB(矩形的对角相等)
,'AB升DC(矩形的对边平元)
∠ABC
∠BCD=180°
又,∠ABC
∠CDA=∠DAB=90
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
