2021-2022学年苏科版八年级数学下册9.4矩形、菱形、正方形强化训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册9.4矩形、菱形、正方形强化训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 670.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 18:35:07 | ||
图片预览



文档简介
2021-2022学年苏科版八年级数学下《9.4 矩形、菱形、正方形》强化训练(四)
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共36分)
1.如图,在 ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定 ABCD是菱形的只有( )
A. AC⊥BD B. AB=BC C. AC=BD D. ∠1=∠2
第1题图 第2题图 第4题图 第6题图
2.如图,在△ABC中,D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
3.在平面直角坐标系中,四边形ABCD的顶点的坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是( )
A. 矩形 B. 菱形 C. 正方形 D. 梯形
4.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于AB的长为半径画弧,分别交于点C,D,连结CD,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
5.下列命题中,是真命题的是( )
A.对角线互相垂直且相等的四边形是菱形 B.对角线互相垂直的平行四边形是菱形
C.对角线互相平分且相等的四边形是菱形 D.对角线互相垂直的四边形是菱形
6.如图,有下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.添加一个条件,能使 ABCD是菱形的有( )
A.①或③ B.②或③ C.③或④ D.①或②或③
7.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于AB的线段长为半径画弧,分别交于点C,D,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
8. 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,则∠CDF等于( )
A.50° B.60° C.70° D.80°
第7题图 第8题图 第9题图 第10题图 第11题图
9.如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )
A.1 B. C.2 D.
10.如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A′E′F′.设P,P′分别是 EF,E′F′的中点,当点A′与点B重合时,四边形PP′CD的面积为( )
A.28 B.24 C.32 D.32-8
11.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于E点,则下列式子不成立的是( )
A.DA=DE B.DB=CE C.∠EAC=90° D.∠ABC=2∠E
12.用尺规在一个平行四边形内作菱形ABCD,下列作法中,错误的是( )
A B C D
二.题空题(每小题3分 共24分)
13.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为____.
第13题图 第14题图
14.如图,在△ABC中,AB=AC,DE垂直平分腰AB.若AC=CD,AB∥CD,则∠A的度数为____.
15.四个点A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD=BC;⑤AD∥BC.这5个条件中任选三个,能使四边形ABCD是菱形的选法有________.
16.在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为________.
17.如图,在△ABC中,AC=BC=2,AB=1,将它沿AB翻折得到△ABD,则四边形ADBC的形状是 形,点P,E,F分别为线段AB,AD,DB上的任意一点,则PE+PF的最小值是 .
第17题图 第19题图 第20题图
18.菱形ABCD的周长为32cm,则菱形ABCD的面积的最大值是 64 cm2.
19. 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是_______.
20、如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为 .
三.解答题(60分)
21.(6分)如图,在△ABC中,M是AC边上的一点,连结BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.
22.(6分)如图,在△ABC中,∠ACB=90°,BF平分∠ABC,CD⊥AB于点D,与BF交于点G,GE∥AC.求证:CE与FG互相垂直平分.
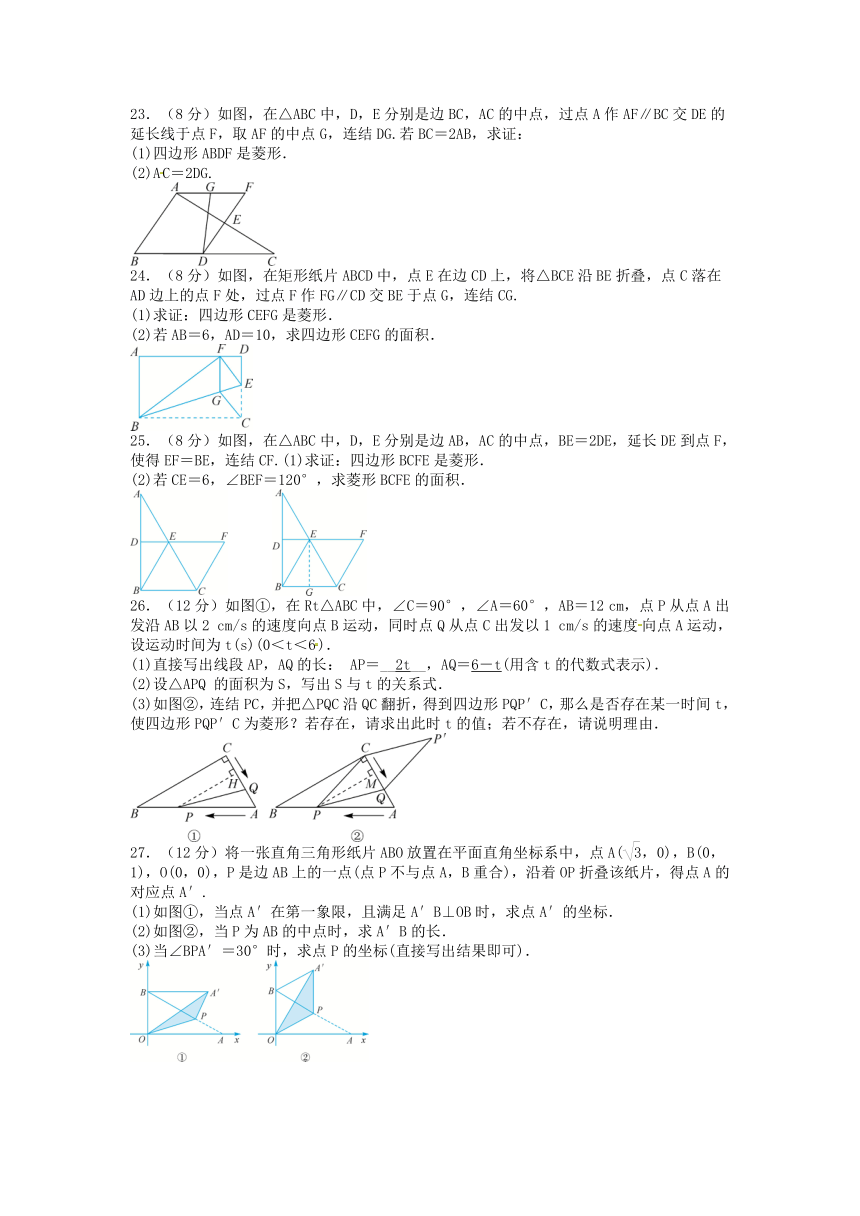
23.(8分)如图,在△ABC中,D,E分别是边BC,AC的中点,过点A作AF∥BC交DE的延长线于点F,取AF的中点G,连结DG.若BC=2AB,求证:
(1)四边形ABDF是菱形.
(2)AC=2DG.
24.(8分)如图,在矩形纸片ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连结CG.
(1)求证:四边形CEFG是菱形.
(2)若AB=6,AD=10,求四边形CEFG的面积.
25.(8分)如图,在△ABC中,D,E分别是边AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连结CF.(1)求证:四边形BCFE是菱形.
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.
26.(12分)如图①,在Rt△ABC中,∠C=90°,∠A=60°,AB=12 cm,点P从点A出发沿AB以2 cm/s的速度向点B运动,同时点Q从点C出发以1 cm/s的速度向点A运动,设运动时间为t(s)(0<t<6).
(1)直接写出线段AP,AQ的长: AP=__2t__,AQ=6-t(用含t的代数式表示).
(2)设△APQ 的面积为S,写出S与t的关系式.
(3)如图②,连结PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时间t,使四边形PQP′C为菱形?若存在,请求出此时t的值;若不存在,请说明理由.
27.(12分)将一张直角三角形纸片ABO放置在平面直角坐标系中,点A(,0),B(0,1),O(0,0),P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点A′.
(1)如图①,当点A′在第一象限,且满足A′B⊥OB时,求点A′的坐标.
(2)如图②,当P为AB的中点时,求A′B的长.
(3)当∠BPA′=30°时,求点P的坐标(直接写出结果即可).
教师样卷
一.选择题(每小题3分 共36分)
1.如图,在 ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定 ABCD是菱形的只有(C)
A. AC⊥BD B. AB=BC C. AC=BD D. ∠1=∠2
第1题图 第2题图 第4题图 第6题图
2.如图,在△ABC中,D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是(D)
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
3.在平面直角坐标系中,四边形ABCD的顶点的坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是(B)
A. 矩形 B. 菱形 C. 正方形 D. 梯形
4.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于AB的长为半径画弧,分别交于点C,D,连结CD,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是(B)
A.矩形 B.菱形 C.正方形 D.等腰梯形
5.下列命题中,是真命题的是(B)
A.对角线互相垂直且相等的四边形是菱形 B.对角线互相垂直的平行四边形是菱形
C.对角线互相平分且相等的四边形是菱形 D.对角线互相垂直的四边形是菱形
6.如图,有下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.添加一个条件,能使 ABCD是菱形的有(A)
A.①或③ B.②或③ C.③或④ D.①或②或③
7.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于AB的线段长为半径画弧,分别交于点C,D,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是(B)
A.矩形 B.菱形 C.正方形 D.等腰梯形
8. 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,则∠CDF等于( B )
A.50° B.60° C.70° D.80°
第7题图 第8题图 第9题图 第10题图 第11题图
9.如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( B )
A.1 B. C.2 D.
10.如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A′E′F′.设P,P′分别是 EF,E′F′的中点,当点A′与点B重合时,四边形PP′CD的面积为( A )
A.28 B.24 C.32 D.32-8
11.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于E点,则下列式子不成立的是( B )
A.DA=DE B.DB=CE C.∠EAC=90° D.∠ABC=2∠E
12.用尺规在一个平行四边形内作菱形ABCD,下列作法中,错误的是(C)
A B C D
二.题空题(每小题3分 共24分)
13.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为____.
第13题图 第14题图
如图,在△ABC中,AB=AC,DE垂直平分腰AB.若AC=CD,AB∥CD,则∠A的度数为__120°__.
15.四个点A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD=BC;⑤AD∥BC.这5个条件中任选三个,能使四边形ABCD是菱形的选法有__4种_____.
16.在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为________.
【答案】105°或45° 【解析】如解图,∵四边形ABCD是菱形,∠A=30°,∴∠ABC=150°,∠ABD=∠DBC=75°,且顶角为120°的等腰三角形的底角是30°.分为以下两种情况:(1)当点E在△ABD内时,∠E1BC=∠E1BD+∠DBC=30°+75°=105°;(2)当点E在△DBC内时,∠E2BC=∠DBC-∠E2BD=75°-30°=45°.综上所述,∠EBC的度数为105°或45°.
17.如图,在△ABC中,AC=BC=2,AB=1,将它沿AB翻折得到△ABD,则四边形ADBC的形状是 形,点P,E,F分别为线段AB,AD,DB上的任意一点,则PE+PF的最小值是 .
【答案】菱 [解析]∵AC=BC,∴△ABC是等腰三角形.将△ABC沿AB翻折得到△ABD,∴AC=BC=AD=BD,∴四边形ADBC是菱形.∵△ABC沿AB翻折得到△ABD,∴△ABC与△ABD关于AB成轴对称.如图所示,作点E关于AB的对称点E',连接PE',根据轴对称的性质知AB垂直平分EE',∴PE=PE',∴PE+PF=PE'+PF,当E',P,F三点共线,且E'F⊥AC时,PE+PF有最小值,该最小值即为平行线AC与BD间的距离.作CM⊥AB于M,BG⊥AD于G,由题知AC=BC=2,AB=1,∠CAB=∠BAD,∴cos∠CAB=cos∠BAD,即=,∴AG=,在Rt△ABG中,BG===,
由对称性可知BG长即为平行线AC,BD间的距离,∴PE+PF的最小值=.
第17题图 第19题图 第20题图
18.菱形ABCD的周长为32cm,则菱形ABCD的面积的最大值是 64 cm2.
19. 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是_______.
20、如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为 62° .
三.解答题(60分)
21.(6分)如图,在△ABC中,M是AC边上的一点,连结BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.
【解】 ∵△ADC是由△ABC翻折得到的,∴∠CAB=∠CAD,AB=AD,BM=DM.
∵AB∥DM, ∴∠BAM=∠AMD,∴∠DAM=∠AMD,∴DA=DM=AB=BM,
∴四边形ABMD是菱形.
22.(6分)如图,在△ABC中,∠ACB=90°,BF平分∠ABC,CD⊥AB于点D,与BF交于点G,GE∥AC.求证:CE与FG互相垂直平分.
【解】 ∵BF平分∠ABC,∴∠CBF=∠ABF.∵CD⊥AB,∠ACB=90°,∴∠CBF+∠BFC=90°,∠ABF+∠BGD=90°,∴∠BGD=∠BFC.∵∠BGD=∠CGF,∴∠BFC=∠CGF,∴CG=CF.∵GE∥AC,∴∠BFC=∠EGF,∴∠CGF=∠EGF,∴∠BGC=∠BGE.又∵BG=BG,∠CBF=∠ABF,∴△BGC≌△BGE(ASA).∴CG=EG.∴CF=GE.又∵GE∥CF,∴四边形CGEF是平行四边形.又∵CG=EG,∴四边形CGEF是菱形,∴CE与FG互相垂直平分.
23.(8分)如图,在△ABC中,D,E分别是边BC,AC的中点,过点A作AF∥BC交DE的延长线于点F,取AF的中点G,连结DG.若BC=2AB,求证:
(1)四边形ABDF是菱形.
(2)AC=2DG.
【解】 (1)∵D,E分别是边BC,AC的中点,∴DE是△ABC的中位线,
∴DE∥AB,DE=AB.∵AF∥BC,∴四边形ABDF是平行四边形.∵BC=2AB,BC=2BD,∴AB=BD.∴ ABDF是菱形.
(2)∵四边形ABDF是菱形,∴AF=AB=DF.∵DE=AB,∴EF=AF. ∵G是AF的中点.∴GF=AF,∴GF=EF.又∵∠F=∠F,∴△FGD≌△FEA(SAS).∴DG=AE.∵AC=2AE,∴AC=2DG.
24.(8分)如图,在矩形纸片ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连结CG.
(1)求证:四边形CEFG是菱形.
(2)若AB=6,AD=10,求四边形CEFG的面积.
【解】 (1)由题意,得△BCE≌△BFE,∴∠BEC=∠BEF,FE=CE.∵FG∥CE,∴∠FGE=∠CEB,∴∠FGE=∠FEG,∴FG=FE,∴FG=EC,∴四边形CEFG是平行四边形.
又∵CE=FE,∴ CEFG是菱形.
(2)∵四边形ABCD是矩形,∴∠BAF=90°,BF=BC=AD=10,∴AF==8,∴DF=2.设EF=x,则CE=x,DE=6-x.∵∠FDE=90°,∴22+(6-x)2=x2,解得x=,∴CE=,∴四边形CEFG的面积=CE·DF=×2=.
25.(8分)如图,在△ABC中,D,E分别是边AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连结CF.(1)求证:四边形BCFE是菱形.
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.
【解】 (1)∵D,E分别是边AB,AC的中点,∴DE∥BC且2DE=BC.又∵BE=2DE,EF=BE,∴EF=BC.又∵EF∥BC,∴四边形BCFE是平行四边形.又∵EF=BE,∴ BCFE是菱形. (2)∵∠BEF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴BE=BC=CE=6.如解图,过点E作EG⊥BC于点G.易得EG=BE=6×=3,∴S菱形BCFE=BC·EG=6×3=18.
26.(12分)如图①,在Rt△ABC中,∠C=90°,∠A=60°,AB=12 cm,点P从点A出发沿AB以2 cm/s的速度向点B运动,同时点Q从点C出发以1 cm/s的速度向点A运动,设运动时间为t(s)(0<t<6).
(1)直接写出线段AP,AQ的长: AP=__2t__,AQ=6-t(用含t的代数式表示).
(2)设△APQ 的面积为S,写出S与t的关系式.
(3)如图②,连结PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时间t,使四边形PQP′C为菱形?若存在,请求出此时t的值;若不存在,请说明理由.
【解】 (1)∵∠C=90°,∠A=60°,∴∠B=30°.又∵AB=12 cm,∴AC=6 cm.由题意,得AP=2t,AQ=6-t.
(2)过点P作PH⊥AC于点H.在Rt△APH中,∵∠A=60°,∴∠HPA=30°.∵AP=2t,∴AH=t.∴PH=t.[]∴S=AQ·PH=(6-t)×t=-t2+3t(0(3)存在.过点P作PM⊥AC于点M.由(2)可知,AM=AP=t,∴QC=AM,∴AQ=CM.
当四边形PQP′C为菱形时,PC=PQ,此时CM=MQ,∴AQ=CM=MQ=AC=2 cm,
此时6-t=2,解得t=4,即当t=4时,四边形PQP′C是菱形.
27.(12分)将一张直角三角形纸片ABO放置在平面直角坐标系中,点A(,0),B(0,1),O(0,0),P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点A′.
(1)如图①,当点A′在第一象限,且满足A′B⊥OB时,求点A′的坐标.
(2)如图②,当P为AB的中点时,求A′B的长.
(3)当∠BPA′=30°时,求点P的坐标(直接写出结果即可).
【解】 (1)∵点A(,0),B(0,1),∴OA=,OB=1.由折叠的性质,得△A′OP≌△AOP,∴OA′=OA=.∵A′B⊥OB,∴∠A′BO=90°,∴在Rt△A′OB中,A′B==,∴点A′的坐标为(,1).
(2)在Rt△AOB中,∵OA=,OB=1,∴AB==2.∵P为AB的中点,∴OP=AP=BP=AB=1,∴OP=OB=BP,∴△BOP是等边三角形,∴∠BOP=∠BPO=60°,
∴∠OPA=180°-∠BPO=120°.由(1)知,△A′OP≌△AOP,∴∠OPA′=∠OPA=120°,PA′=PA=1,∴OB∥PA′.又∵OB=PA′=1,∴四边形OPA′B是平行四边形,∴A′B=OP=1.
(3)分两种情况讨论:①当点A′在直线BP的上方时,如解图①.∵∠BPA′=30°,∴∠APO+∠A′PO=210°.又∵∠APO=∠A′PO,∴∠APO=105°.又∵∠OAP=30°,∴∠AOP=45°.
过点P作PC⊥OA于点C,设OC=x,则PC=x,AC=x.∵OA=,∴x+x=,解得x=,∴点P.②当点A′在直线BP的下方时,如解图②.∵∠BPA′=30°,∴∠APO+∠A′PO=150°.又∵∠APO=∠A′PO,∴∠APO=75°.又∵∠OAP=30°,∴∠AOP=75°,∴∠APO=∠AOP,∴PA=OA=.过点P作PD⊥OA于点D.∵∠OAP=30°,∴PD=PA=,∴AD=,
∴OD=,∴点P.综上所述,当∠BPA′=30°时,点P的坐标为或.
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共36分)
1.如图,在 ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定 ABCD是菱形的只有( )
A. AC⊥BD B. AB=BC C. AC=BD D. ∠1=∠2
第1题图 第2题图 第4题图 第6题图
2.如图,在△ABC中,D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
3.在平面直角坐标系中,四边形ABCD的顶点的坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是( )
A. 矩形 B. 菱形 C. 正方形 D. 梯形
4.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于AB的长为半径画弧,分别交于点C,D,连结CD,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
5.下列命题中,是真命题的是( )
A.对角线互相垂直且相等的四边形是菱形 B.对角线互相垂直的平行四边形是菱形
C.对角线互相平分且相等的四边形是菱形 D.对角线互相垂直的四边形是菱形
6.如图,有下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.添加一个条件,能使 ABCD是菱形的有( )
A.①或③ B.②或③ C.③或④ D.①或②或③
7.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于AB的线段长为半径画弧,分别交于点C,D,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
8. 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,则∠CDF等于( )
A.50° B.60° C.70° D.80°
第7题图 第8题图 第9题图 第10题图 第11题图
9.如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )
A.1 B. C.2 D.
10.如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A′E′F′.设P,P′分别是 EF,E′F′的中点,当点A′与点B重合时,四边形PP′CD的面积为( )
A.28 B.24 C.32 D.32-8
11.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于E点,则下列式子不成立的是( )
A.DA=DE B.DB=CE C.∠EAC=90° D.∠ABC=2∠E
12.用尺规在一个平行四边形内作菱形ABCD,下列作法中,错误的是( )
A B C D
二.题空题(每小题3分 共24分)
13.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为____.
第13题图 第14题图
14.如图,在△ABC中,AB=AC,DE垂直平分腰AB.若AC=CD,AB∥CD,则∠A的度数为____.
15.四个点A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD=BC;⑤AD∥BC.这5个条件中任选三个,能使四边形ABCD是菱形的选法有________.
16.在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为________.
17.如图,在△ABC中,AC=BC=2,AB=1,将它沿AB翻折得到△ABD,则四边形ADBC的形状是 形,点P,E,F分别为线段AB,AD,DB上的任意一点,则PE+PF的最小值是 .
第17题图 第19题图 第20题图
18.菱形ABCD的周长为32cm,则菱形ABCD的面积的最大值是 64 cm2.
19. 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是_______.
20、如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为 .
三.解答题(60分)
21.(6分)如图,在△ABC中,M是AC边上的一点,连结BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.
22.(6分)如图,在△ABC中,∠ACB=90°,BF平分∠ABC,CD⊥AB于点D,与BF交于点G,GE∥AC.求证:CE与FG互相垂直平分.
23.(8分)如图,在△ABC中,D,E分别是边BC,AC的中点,过点A作AF∥BC交DE的延长线于点F,取AF的中点G,连结DG.若BC=2AB,求证:
(1)四边形ABDF是菱形.
(2)AC=2DG.
24.(8分)如图,在矩形纸片ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连结CG.
(1)求证:四边形CEFG是菱形.
(2)若AB=6,AD=10,求四边形CEFG的面积.
25.(8分)如图,在△ABC中,D,E分别是边AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连结CF.(1)求证:四边形BCFE是菱形.
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.
26.(12分)如图①,在Rt△ABC中,∠C=90°,∠A=60°,AB=12 cm,点P从点A出发沿AB以2 cm/s的速度向点B运动,同时点Q从点C出发以1 cm/s的速度向点A运动,设运动时间为t(s)(0<t<6).
(1)直接写出线段AP,AQ的长: AP=__2t__,AQ=6-t(用含t的代数式表示).
(2)设△APQ 的面积为S,写出S与t的关系式.
(3)如图②,连结PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时间t,使四边形PQP′C为菱形?若存在,请求出此时t的值;若不存在,请说明理由.
27.(12分)将一张直角三角形纸片ABO放置在平面直角坐标系中,点A(,0),B(0,1),O(0,0),P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点A′.
(1)如图①,当点A′在第一象限,且满足A′B⊥OB时,求点A′的坐标.
(2)如图②,当P为AB的中点时,求A′B的长.
(3)当∠BPA′=30°时,求点P的坐标(直接写出结果即可).
教师样卷
一.选择题(每小题3分 共36分)
1.如图,在 ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定 ABCD是菱形的只有(C)
A. AC⊥BD B. AB=BC C. AC=BD D. ∠1=∠2
第1题图 第2题图 第4题图 第6题图
2.如图,在△ABC中,D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是(D)
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
3.在平面直角坐标系中,四边形ABCD的顶点的坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是(B)
A. 矩形 B. 菱形 C. 正方形 D. 梯形
4.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于AB的长为半径画弧,分别交于点C,D,连结CD,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是(B)
A.矩形 B.菱形 C.正方形 D.等腰梯形
5.下列命题中,是真命题的是(B)
A.对角线互相垂直且相等的四边形是菱形 B.对角线互相垂直的平行四边形是菱形
C.对角线互相平分且相等的四边形是菱形 D.对角线互相垂直的四边形是菱形
6.如图,有下列条件:①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.添加一个条件,能使 ABCD是菱形的有(A)
A.①或③ B.②或③ C.③或④ D.①或②或③
7.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于AB的线段长为半径画弧,分别交于点C,D,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是(B)
A.矩形 B.菱形 C.正方形 D.等腰梯形
8. 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,则∠CDF等于( B )
A.50° B.60° C.70° D.80°
第7题图 第8题图 第9题图 第10题图 第11题图
9.如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( B )
A.1 B. C.2 D.
10.如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A′E′F′.设P,P′分别是 EF,E′F′的中点,当点A′与点B重合时,四边形PP′CD的面积为( A )
A.28 B.24 C.32 D.32-8
11.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于E点,则下列式子不成立的是( B )
A.DA=DE B.DB=CE C.∠EAC=90° D.∠ABC=2∠E
12.用尺规在一个平行四边形内作菱形ABCD,下列作法中,错误的是(C)
A B C D
二.题空题(每小题3分 共24分)
13.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为____.
第13题图 第14题图
如图,在△ABC中,AB=AC,DE垂直平分腰AB.若AC=CD,AB∥CD,则∠A的度数为__120°__.
15.四个点A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD=BC;⑤AD∥BC.这5个条件中任选三个,能使四边形ABCD是菱形的选法有__4种_____.
16.在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为________.
【答案】105°或45° 【解析】如解图,∵四边形ABCD是菱形,∠A=30°,∴∠ABC=150°,∠ABD=∠DBC=75°,且顶角为120°的等腰三角形的底角是30°.分为以下两种情况:(1)当点E在△ABD内时,∠E1BC=∠E1BD+∠DBC=30°+75°=105°;(2)当点E在△DBC内时,∠E2BC=∠DBC-∠E2BD=75°-30°=45°.综上所述,∠EBC的度数为105°或45°.
17.如图,在△ABC中,AC=BC=2,AB=1,将它沿AB翻折得到△ABD,则四边形ADBC的形状是 形,点P,E,F分别为线段AB,AD,DB上的任意一点,则PE+PF的最小值是 .
【答案】菱 [解析]∵AC=BC,∴△ABC是等腰三角形.将△ABC沿AB翻折得到△ABD,∴AC=BC=AD=BD,∴四边形ADBC是菱形.∵△ABC沿AB翻折得到△ABD,∴△ABC与△ABD关于AB成轴对称.如图所示,作点E关于AB的对称点E',连接PE',根据轴对称的性质知AB垂直平分EE',∴PE=PE',∴PE+PF=PE'+PF,当E',P,F三点共线,且E'F⊥AC时,PE+PF有最小值,该最小值即为平行线AC与BD间的距离.作CM⊥AB于M,BG⊥AD于G,由题知AC=BC=2,AB=1,∠CAB=∠BAD,∴cos∠CAB=cos∠BAD,即=,∴AG=,在Rt△ABG中,BG===,
由对称性可知BG长即为平行线AC,BD间的距离,∴PE+PF的最小值=.
第17题图 第19题图 第20题图
18.菱形ABCD的周长为32cm,则菱形ABCD的面积的最大值是 64 cm2.
19. 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是_______.
20、如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为 62° .
三.解答题(60分)
21.(6分)如图,在△ABC中,M是AC边上的一点,连结BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.
【解】 ∵△ADC是由△ABC翻折得到的,∴∠CAB=∠CAD,AB=AD,BM=DM.
∵AB∥DM, ∴∠BAM=∠AMD,∴∠DAM=∠AMD,∴DA=DM=AB=BM,
∴四边形ABMD是菱形.
22.(6分)如图,在△ABC中,∠ACB=90°,BF平分∠ABC,CD⊥AB于点D,与BF交于点G,GE∥AC.求证:CE与FG互相垂直平分.
【解】 ∵BF平分∠ABC,∴∠CBF=∠ABF.∵CD⊥AB,∠ACB=90°,∴∠CBF+∠BFC=90°,∠ABF+∠BGD=90°,∴∠BGD=∠BFC.∵∠BGD=∠CGF,∴∠BFC=∠CGF,∴CG=CF.∵GE∥AC,∴∠BFC=∠EGF,∴∠CGF=∠EGF,∴∠BGC=∠BGE.又∵BG=BG,∠CBF=∠ABF,∴△BGC≌△BGE(ASA).∴CG=EG.∴CF=GE.又∵GE∥CF,∴四边形CGEF是平行四边形.又∵CG=EG,∴四边形CGEF是菱形,∴CE与FG互相垂直平分.
23.(8分)如图,在△ABC中,D,E分别是边BC,AC的中点,过点A作AF∥BC交DE的延长线于点F,取AF的中点G,连结DG.若BC=2AB,求证:
(1)四边形ABDF是菱形.
(2)AC=2DG.
【解】 (1)∵D,E分别是边BC,AC的中点,∴DE是△ABC的中位线,
∴DE∥AB,DE=AB.∵AF∥BC,∴四边形ABDF是平行四边形.∵BC=2AB,BC=2BD,∴AB=BD.∴ ABDF是菱形.
(2)∵四边形ABDF是菱形,∴AF=AB=DF.∵DE=AB,∴EF=AF. ∵G是AF的中点.∴GF=AF,∴GF=EF.又∵∠F=∠F,∴△FGD≌△FEA(SAS).∴DG=AE.∵AC=2AE,∴AC=2DG.
24.(8分)如图,在矩形纸片ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连结CG.
(1)求证:四边形CEFG是菱形.
(2)若AB=6,AD=10,求四边形CEFG的面积.
【解】 (1)由题意,得△BCE≌△BFE,∴∠BEC=∠BEF,FE=CE.∵FG∥CE,∴∠FGE=∠CEB,∴∠FGE=∠FEG,∴FG=FE,∴FG=EC,∴四边形CEFG是平行四边形.
又∵CE=FE,∴ CEFG是菱形.
(2)∵四边形ABCD是矩形,∴∠BAF=90°,BF=BC=AD=10,∴AF==8,∴DF=2.设EF=x,则CE=x,DE=6-x.∵∠FDE=90°,∴22+(6-x)2=x2,解得x=,∴CE=,∴四边形CEFG的面积=CE·DF=×2=.
25.(8分)如图,在△ABC中,D,E分别是边AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连结CF.(1)求证:四边形BCFE是菱形.
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.
【解】 (1)∵D,E分别是边AB,AC的中点,∴DE∥BC且2DE=BC.又∵BE=2DE,EF=BE,∴EF=BC.又∵EF∥BC,∴四边形BCFE是平行四边形.又∵EF=BE,∴ BCFE是菱形. (2)∵∠BEF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴BE=BC=CE=6.如解图,过点E作EG⊥BC于点G.易得EG=BE=6×=3,∴S菱形BCFE=BC·EG=6×3=18.
26.(12分)如图①,在Rt△ABC中,∠C=90°,∠A=60°,AB=12 cm,点P从点A出发沿AB以2 cm/s的速度向点B运动,同时点Q从点C出发以1 cm/s的速度向点A运动,设运动时间为t(s)(0<t<6).
(1)直接写出线段AP,AQ的长: AP=__2t__,AQ=6-t(用含t的代数式表示).
(2)设△APQ 的面积为S,写出S与t的关系式.
(3)如图②,连结PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时间t,使四边形PQP′C为菱形?若存在,请求出此时t的值;若不存在,请说明理由.
【解】 (1)∵∠C=90°,∠A=60°,∴∠B=30°.又∵AB=12 cm,∴AC=6 cm.由题意,得AP=2t,AQ=6-t.
(2)过点P作PH⊥AC于点H.在Rt△APH中,∵∠A=60°,∴∠HPA=30°.∵AP=2t,∴AH=t.∴PH=t.[]∴S=AQ·PH=(6-t)×t=-t2+3t(0
当四边形PQP′C为菱形时,PC=PQ,此时CM=MQ,∴AQ=CM=MQ=AC=2 cm,
此时6-t=2,解得t=4,即当t=4时,四边形PQP′C是菱形.
27.(12分)将一张直角三角形纸片ABO放置在平面直角坐标系中,点A(,0),B(0,1),O(0,0),P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点A′.
(1)如图①,当点A′在第一象限,且满足A′B⊥OB时,求点A′的坐标.
(2)如图②,当P为AB的中点时,求A′B的长.
(3)当∠BPA′=30°时,求点P的坐标(直接写出结果即可).
【解】 (1)∵点A(,0),B(0,1),∴OA=,OB=1.由折叠的性质,得△A′OP≌△AOP,∴OA′=OA=.∵A′B⊥OB,∴∠A′BO=90°,∴在Rt△A′OB中,A′B==,∴点A′的坐标为(,1).
(2)在Rt△AOB中,∵OA=,OB=1,∴AB==2.∵P为AB的中点,∴OP=AP=BP=AB=1,∴OP=OB=BP,∴△BOP是等边三角形,∴∠BOP=∠BPO=60°,
∴∠OPA=180°-∠BPO=120°.由(1)知,△A′OP≌△AOP,∴∠OPA′=∠OPA=120°,PA′=PA=1,∴OB∥PA′.又∵OB=PA′=1,∴四边形OPA′B是平行四边形,∴A′B=OP=1.
(3)分两种情况讨论:①当点A′在直线BP的上方时,如解图①.∵∠BPA′=30°,∴∠APO+∠A′PO=210°.又∵∠APO=∠A′PO,∴∠APO=105°.又∵∠OAP=30°,∴∠AOP=45°.
过点P作PC⊥OA于点C,设OC=x,则PC=x,AC=x.∵OA=,∴x+x=,解得x=,∴点P.②当点A′在直线BP的下方时,如解图②.∵∠BPA′=30°,∴∠APO+∠A′PO=150°.又∵∠APO=∠A′PO,∴∠APO=75°.又∵∠OAP=30°,∴∠AOP=75°,∴∠APO=∠AOP,∴PA=OA=.过点P作PD⊥OA于点D.∵∠OAP=30°,∴PD=PA=,∴AD=,
∴OD=,∴点P.综上所述,当∠BPA′=30°时,点P的坐标为或.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
