2021—2022学年人教版九年级数学下册27.2.1相似三角形的判定练习题(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册27.2.1相似三角形的判定练习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 234.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 22:55:47 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学下册 第二十七章 相似
27.2.1相似三角形的判定 练习题
一、选择题
1.下列各组图形中,不一定相似的是( )
A.任意两个等腰直角三角形 B.任意两个等边三角形
C.任意两个矩形 D.任意两个正方形
2.下列不能判定和以,,为顶点的三角形相似的条件是( )
A. B.且
C.且 D.且
3.如图,D,E分别是△ABC的边AB,AC上的点,连接DE,下列条件不能判定△ADE与△ABC相似的是( )
A.∠ADE=∠B B.∠AED=∠C C. D.
4.如图,甲、乙中各有两个三角形,其边长和角的度数如图上标注,则对甲、乙中两个三角形,下列说法正确的是( )
A.都相似 B.都不相似 C.只有甲中两个三角形相似 D.只有乙中两个三角形相似
5.如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )
A. B. C.是的中点 D.
6.如图,点P在的边上,要判断,添加一个条件错误的是( )
A. B. C. D.
7.如图,已知矩形ABCD中,点E是边AD上的任一点,连接BE,过E作BE的垂线交BC延长线于点F,交边CD于点P,则图中共有相似三角形( )
A.6对 B.5对 C.4对 D.3对
8.如图,在中,点、分别在边、上,下列条件中能判断的是( )
①;②;③;④.
A.①② B.①②③
C.①②④ D.①②③④
9.如图,在正方形中,为中点,. 联结.那么下列结果错误的是( )
A.与相似 B.与相似 C.与相似 D.△AEF与△ECF相似
10.如图,在正方形ABCD中,点E为AD边上的一个动点(与点A,D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线AC于点G,交CD于点M,下列结论中错误的是( )
A.△AEF∽△CBF B.△CMG∽△BFG C.△ABF∽△CBG D.△BDE∽△BCG
二、填空题
11.如图,已知=,若使△ABC∽△ADE成立_____(只添一种即可).
12.如图,AC与BD相交于点O,在△AOB和△DOC中,已知,又因为________可证明△AOB∽△DOC.
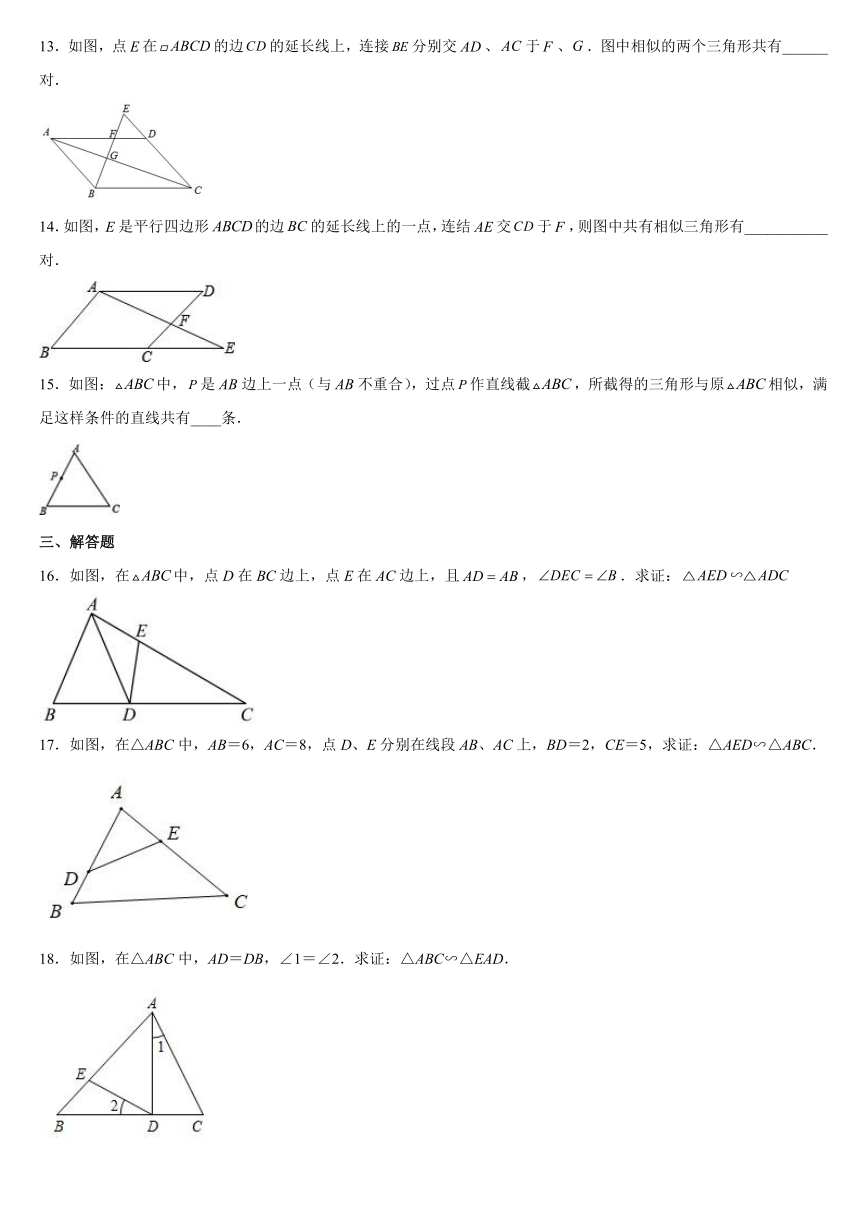
13.如图,点在的边的延长线上,连接分别交、于、.图中相似的两个三角形共有______对.
14.如图,是平行四边形的边的延长线上的一点,连结交于,则图中共有相似三角形有___________对.
15.如图:中,是AB边上一点(与AB不重合),过点作直线截,所截得的三角形与原相似,满足这样条件的直线共有____条.
三、解答题
16.如图,在中,点D在BC边上,点E在AC边上,且,.求证:
17.如图,在△ABC中,AB=6,AC=8,点D、E分别在线段AB、AC上,BD=2,CE=5,求证:△AED∽△ABC.
18.如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
19.如图,,垂足为D,,垂足为E,AD与BE相交于点F,连接ED.你能在图中找出一对相似三角形,并说明相似的理由吗?
20.如图,在四边形中,,对角线与相交于点O.找出图中的相似三角形,并说明理由.
21.如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠A=∠BPD,求证:△APC∽△BPD.
22.如图,在Rt△ABC中,∠C=90°,D是AB上一点,E是BC上一点,AC=6,BC=8,BD=4,BE=5.求证:DE⊥AB.
23.如图,中,CD是斜边AB上的高.求证:
(1);
(2).
【参考答案】
1.C 2.D 3.D 4.C 5.C 6.D 7.A 8.B 9.C 10.C
11.∠DAE=∠BAC(不唯一)
12.∠AOB=∠DOC
13.6
14.3
15.4
16.∵AB=AD
∴∠B=∠ADB
∵∠DEC=∠B
∴∠ADB=∠DEC
∴∠AED=∠ADC
又∵∠DAE=∠CAD
∴
17.证明:∵AB=6,AC=8,BD=2,CE=5,
∴,,
∵,,
∴,
又∵∠DAE=∠CAB,
∴△AED∽△ABC.
18.证明:∵AD=DB,
∴∠B=∠BAD.
∵∠BDA=∠1+∠C=∠2+∠ADE,
又∵∠1=∠2,
∴∠C=∠ADE.
∴△ABC∽△EAD.
19.解:,理由是:
∵,,
∴,
∵,
∴.
(或,等)(答案不唯一).
20解:,理由为:
∵AB∥CD,
∴∠OAB=∠OCD,又∠AOB=∠COD,
∴.
21.证明:∵PC=PD=CD,
∴为等边三角形,
∴∠PCD=∠PDC,
∴,
∵∠A=∠BPD,
∴△APC∽△PBD.
22.证明:∵∠C=90°,AC=6,BC=8,
∴AB=,
∵BD=4,BE=5,
∴,,
∵∠B=∠B,
∴△BDE∽△BCA,
∴∠BDE=∠C=90°,
即DE⊥AB.
23.证明:(1)∵CD是斜边AB上的高,
∴∠ADC=90°,
∴∠ADC=∠ACB=90°,
∵∠A=∠A,
∴△ACD∽△ABC.
(2)∵CD是斜边AB上的高,
∴∠BDC=90°,
∴∠BDC=∠ACB=90°,
∵∠B=∠B,
∴△CBD∽△ABC.
27.2.1相似三角形的判定 练习题
一、选择题
1.下列各组图形中,不一定相似的是( )
A.任意两个等腰直角三角形 B.任意两个等边三角形
C.任意两个矩形 D.任意两个正方形
2.下列不能判定和以,,为顶点的三角形相似的条件是( )
A. B.且
C.且 D.且
3.如图,D,E分别是△ABC的边AB,AC上的点,连接DE,下列条件不能判定△ADE与△ABC相似的是( )
A.∠ADE=∠B B.∠AED=∠C C. D.
4.如图,甲、乙中各有两个三角形,其边长和角的度数如图上标注,则对甲、乙中两个三角形,下列说法正确的是( )
A.都相似 B.都不相似 C.只有甲中两个三角形相似 D.只有乙中两个三角形相似
5.如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )
A. B. C.是的中点 D.
6.如图,点P在的边上,要判断,添加一个条件错误的是( )
A. B. C. D.
7.如图,已知矩形ABCD中,点E是边AD上的任一点,连接BE,过E作BE的垂线交BC延长线于点F,交边CD于点P,则图中共有相似三角形( )
A.6对 B.5对 C.4对 D.3对
8.如图,在中,点、分别在边、上,下列条件中能判断的是( )
①;②;③;④.
A.①② B.①②③
C.①②④ D.①②③④
9.如图,在正方形中,为中点,. 联结.那么下列结果错误的是( )
A.与相似 B.与相似 C.与相似 D.△AEF与△ECF相似
10.如图,在正方形ABCD中,点E为AD边上的一个动点(与点A,D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线AC于点G,交CD于点M,下列结论中错误的是( )
A.△AEF∽△CBF B.△CMG∽△BFG C.△ABF∽△CBG D.△BDE∽△BCG
二、填空题
11.如图,已知=,若使△ABC∽△ADE成立_____(只添一种即可).
12.如图,AC与BD相交于点O,在△AOB和△DOC中,已知,又因为________可证明△AOB∽△DOC.
13.如图,点在的边的延长线上,连接分别交、于、.图中相似的两个三角形共有______对.
14.如图,是平行四边形的边的延长线上的一点,连结交于,则图中共有相似三角形有___________对.
15.如图:中,是AB边上一点(与AB不重合),过点作直线截,所截得的三角形与原相似,满足这样条件的直线共有____条.
三、解答题
16.如图,在中,点D在BC边上,点E在AC边上,且,.求证:
17.如图,在△ABC中,AB=6,AC=8,点D、E分别在线段AB、AC上,BD=2,CE=5,求证:△AED∽△ABC.
18.如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
19.如图,,垂足为D,,垂足为E,AD与BE相交于点F,连接ED.你能在图中找出一对相似三角形,并说明相似的理由吗?
20.如图,在四边形中,,对角线与相交于点O.找出图中的相似三角形,并说明理由.
21.如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠A=∠BPD,求证:△APC∽△BPD.
22.如图,在Rt△ABC中,∠C=90°,D是AB上一点,E是BC上一点,AC=6,BC=8,BD=4,BE=5.求证:DE⊥AB.
23.如图,中,CD是斜边AB上的高.求证:
(1);
(2).
【参考答案】
1.C 2.D 3.D 4.C 5.C 6.D 7.A 8.B 9.C 10.C
11.∠DAE=∠BAC(不唯一)
12.∠AOB=∠DOC
13.6
14.3
15.4
16.∵AB=AD
∴∠B=∠ADB
∵∠DEC=∠B
∴∠ADB=∠DEC
∴∠AED=∠ADC
又∵∠DAE=∠CAD
∴
17.证明:∵AB=6,AC=8,BD=2,CE=5,
∴,,
∵,,
∴,
又∵∠DAE=∠CAB,
∴△AED∽△ABC.
18.证明:∵AD=DB,
∴∠B=∠BAD.
∵∠BDA=∠1+∠C=∠2+∠ADE,
又∵∠1=∠2,
∴∠C=∠ADE.
∴△ABC∽△EAD.
19.解:,理由是:
∵,,
∴,
∵,
∴.
(或,等)(答案不唯一).
20解:,理由为:
∵AB∥CD,
∴∠OAB=∠OCD,又∠AOB=∠COD,
∴.
21.证明:∵PC=PD=CD,
∴为等边三角形,
∴∠PCD=∠PDC,
∴,
∵∠A=∠BPD,
∴△APC∽△PBD.
22.证明:∵∠C=90°,AC=6,BC=8,
∴AB=,
∵BD=4,BE=5,
∴,,
∵∠B=∠B,
∴△BDE∽△BCA,
∴∠BDE=∠C=90°,
即DE⊥AB.
23.证明:(1)∵CD是斜边AB上的高,
∴∠ADC=90°,
∴∠ADC=∠ACB=90°,
∵∠A=∠A,
∴△ACD∽△ABC.
(2)∵CD是斜边AB上的高,
∴∠BDC=90°,
∴∠BDC=∠ACB=90°,
∵∠B=∠B,
∴△CBD∽△ABC.
