人教版七年级数学下册5.3平行线的性质同步练习 (word版含答案)
文档属性
| 名称 | 人教版七年级数学下册5.3平行线的性质同步练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 07:35:14 | ||
图片预览


文档简介
人教版七年级下册 5.3 平行线的性质 同步练习
一、单选题
1.如图,AF是∠BAC的平分线, DF∥AC,若∠1=25°,则∠BDF的度数为( )
A.25° B.50° C.75° D.100°
2.如图,由ABCD,可以得到( )
A. B. C. D.
3.若要说明命题:“如果a<b,那么a2<b2”是假命题,则可以举的反例是( )
A.a=2,b=3 B.a=﹣2,b=﹣3 C.a=﹣3,b=﹣2 D.a=﹣2,b=3
4.下列命题是真命题的个数为( )
①一个角的补角大于这个角.②三角形的内角和是180°.③若,则.④相等的角是对顶角.⑤两点之间,线段最短.
A.2 B.3 C.4 D.5
5.如图,已知AB∥CD,∠1=30°,∠2=90°,则∠3等于( )
A.60° B.50° C.45° D.30°
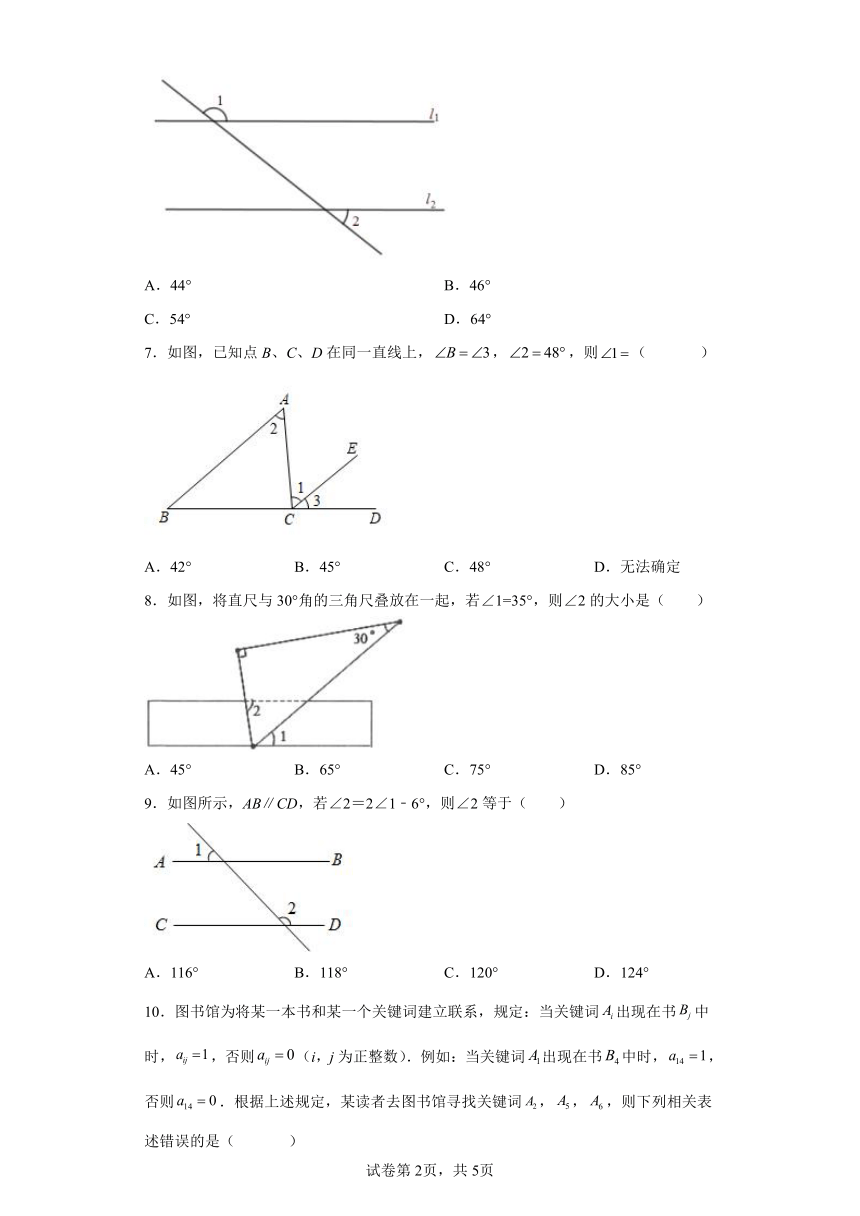
6.如图,直线l1∥l2,∠1=136°,则∠2的度数是( )
A.44° B.46°
C.54° D.64°
7.如图,已知点B、C、D在同一直线上,,,则( )
A.42° B.45° C.48° D.无法确定
8.如图,将直尺与30°角的三角尺叠放在一起,若∠1=35°,则∠2的大小是( )
A.45° B.65° C.75° D.85°
9.如图所示,AB∥CD,若∠2=2∠1﹣6°,则∠2等于( )
A.116° B.118° C.120° D.124°
10.图书馆为将某一本书和某一个关键词建立联系,规定:当关键词出现在书中时,,否则(i,j为正整数).例如:当关键词出现在书中时,,否则.根据上述规定,某读者去图书馆寻找关键词,,,则下列相关表述错误的是( )
A.当时,只需要选择这本书就可以找到所有的关键词
B.当时,从这本书查不到需要的关键词
C.当a2j,a5j,a6j全是1时,可以从这本书查到需要的关键词
D.当时,从这本书一定查不到需要的关键词
二、填空题
11.如图,已知AE∥BC,∠BAC=105°,∠DAE=48°,则∠C=______.
12.将一把直尺与含30°的直角三角板如图摆放,使三角板的一个锐角顶点落在直尺的一边上,若∠1=40°,则∠2=_____°.
13.如图,ABCD,EFCD,平分,,则__.
14.完成下面的证明:
看图填空:已知如图,于,于,,求证:平分.
证明:于,于G(_____),
,(_____).
(_____).
(_____).
_____(_____),
_____(_____).
又(已知),
(_____),
平分(_____).
三、解答题
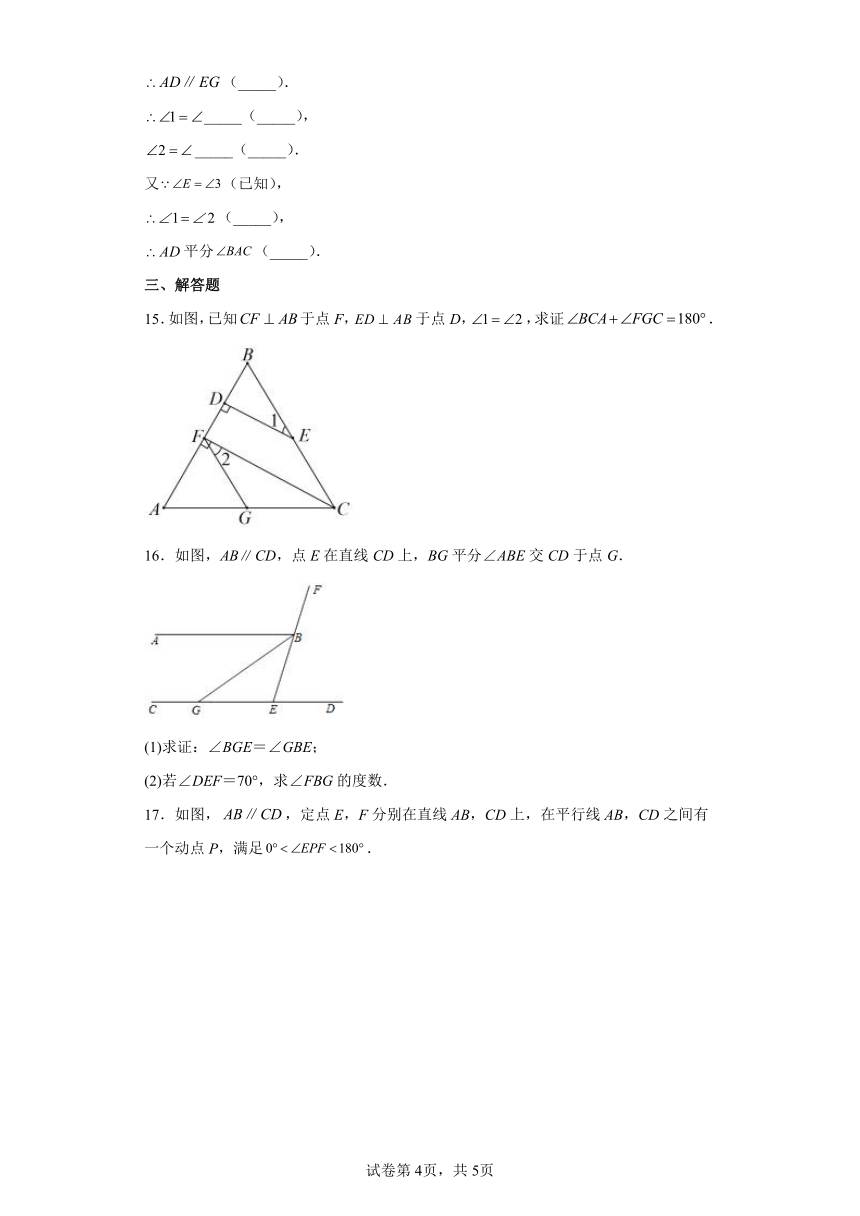
15.如图,已知于点F,于点D,,求证.
16.如图,ABCD,点E在直线CD上,BG平分∠ABE交CD于点G.
(1)求证:∠BGE=∠GBE;
(2)若∠DEF=70°,求∠FBG的度数.
17.如图,,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一个动点P,满足.
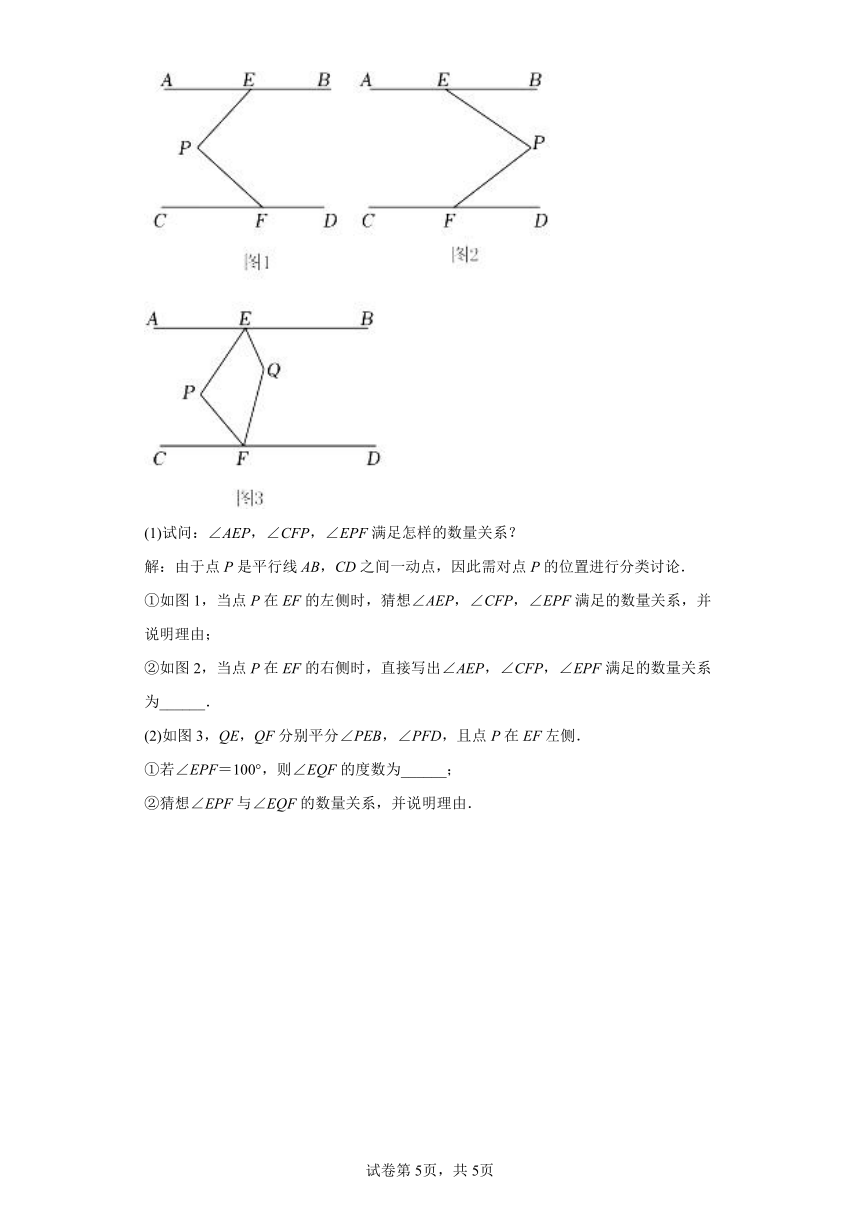
(1)试问:∠AEP,∠CFP,∠EPF满足怎样的数量关系?
解:由于点P是平行线AB,CD之间一动点,因此需对点P的位置进行分类讨论.
①如图1,当点P在EF的左侧时,猜想∠AEP,∠CFP,∠EPF满足的数量关系,并说明理由;
②如图2,当点P在EF的右侧时,直接写出∠AEP,∠CFP,∠EPF满足的数量关系为______.
(2)如图3,QE,QF分别平分∠PEB,∠PFD,且点P在EF左侧.
①若∠EPF=100°,则∠EQF的度数为______;
②猜想∠EPF与∠EQF的数量关系,并说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
根据两直线平行,同位角相等,可得∠FAC=∠1,再根据角平分线的定义可求得∠BAC的度数,再利用平行线的性质可求解.
【详解】
解:∵DF∥AC,
∴∠FAC=∠1=25°,
∵AF是∠BAC的平分线,
∴∠BAF=∠FAC=25°,
∴∠BAC=50°,
∵DF∥AC,
∴∠BDF=∠BAC=50°.
故选:B
【点睛】
本题主要考查了平行线的性质,角平分线的定义,熟练掌握两直线平行,同位角相等是解题的关键.
2.A
【解析】
【分析】
直接利用平行线的性质分析得出答案.
【详解】
解:,
(两直线平行,内错角相等),
故选:A.
【点睛】
此题主要考查了平行线的性质,正确把握平行线的性质是解题关键.
3.C
【解析】
【分析】
逐项进行计算,然后进行判断即可.
【详解】
解:A. a=2,b=3,有a<b, a2<b2,不符合题意;
B. a=﹣2,b=﹣3,有a>b,不符合题意;
C. a=﹣3,b=﹣2,有a<b, a2>b2,符合题意;
D. a=﹣2,b=3有a<b, a2<b2,不符合题意;
故选:C.
【点睛】
本题考查了有理数的运算和假命题的判断,解题关键是熟练进行计算,准确进行判断.
4.A
【解析】
【分析】
根据补角、三角形内角和定理、平方的计算、对顶角的性质及两点之间线段最短依次进行判断即可得出结论.
【详解】
解:①一个角的补角大于这个角,若这个角是钝角,则其补角小于这个角,错误,假命题;
②三角形的内角和是180°,正确,是真命题;
③若,则或,错误,是假命题;
④相等的角不一定是对顶角,错误,假命题;
⑤两点之间,线段最短,正确,真命题;
综上可得:②⑤是真命题,
故选:A.
【点睛】
题目主要考查命题真假的判断,理解题意,熟练掌握各个定理是解题关键.
5.A
【解析】
略
6.A
【解析】
【分析】
根据两直线平行,同位角相等求出∠1的同位角∠3的度数,再根据邻补角进行求解.
【详解】
∵直线l1∥l2,∠1=136°,
∴∠1=∠3=136°
∴∠2=180°-∠3=180°-136°=44°.
故选:A.
【点睛】
本题考查了平行线的性质,熟记性质两直线平行,同位角相等是解题的关键.
7.C
【解析】
【分析】
根据,可得,根据平行线的性质,两直线平行,内错角相等可得
【详解】
解:∵
∴
.
故选C
【点睛】
本题考查了平行线的性质与判定求角度,掌握平行线的性质与判定是解题的关键.
8.D
【解析】
【分析】
根据平角的定义和平行线的性质即可得到结论.
【详解】
解:由题意得,∠4=90°-30°=60°,
∵∠1=35°,
∴∠3=180°-60°-35°=85°,
∵AB∥CD,
∴∠3=∠2=85°,
故选:D.
【点睛】
本题考查了平行线的性质,平角的定义,熟练掌握平行线的性质是解题的关键.
9.B
【解析】
【分析】
由AB与CD平行,利用两直线平行同旁内角互补得到∠2+∠3=180°,由对顶角相等得到∠1=∠3,等量代换得到∠1=180°-∠2,再代入∠2=2∠1﹣6°,即可求出∠2的度数.
【详解】
解:如图:
∵AB∥CD,
∴∠2+∠3=180°,
∴∠3=180°-∠2,
∵∠1=∠3,
∴∠1=180°-∠2,
∴∠2=2(180°-∠2)﹣6°,
∴∠2=118°,
故选:B.
【点睛】
此题考查了对顶角性质和平行线的性质,掌握两直线平行同旁内角互补是解答此题的关键.
10.B
【解析】
【分析】
根据题意aij的值要么为1,要么为0,当关键词Ai出现在书Bj中时,元素aij=1,否则aij=0(i,j为正整数),按照此规定对每个选项分析推理即可.
【详解】
解:根据题意aij的值要么为1,要么为0,
A、a21+a51+a61=3,说明a21=1,a51=1,a61=1,故关键词“A2,A5,A6”同时出现在书B1中,
而读者去图书馆寻找书中同时有关键词“A2,A5,A6”的书,故A表述正确;
B、当a22+a52+a62<3时,则a22、a52、a62是必有值为0的,即关键词“A2,A5,A6”不同时具有,
从而不选择B2这本书,故B表述错误;
C、当a2j,a5j,a6j全是1时,则a2j=1,a5j=1,a6j=1,故关键词“A2,A5,A6”同时出现在书Bj中,
则选择Bj这本书,故C表述正确;
D、根据前述分析可知,只有当a22+a52+a62=3时,才能选择B2这本书,而a22+a52+a62的值可能为0、1、2、3,
故D表述正确.
故选:B.
【点睛】
本题考查了推理与论证,读懂题意,按照规定进行计算与推理是解题的关键.
11.27°
【解析】
【分析】
利用平角定义求出∠EAC的度数,根据,求出∠C.
【详解】
解:∵∠BAC=105°,∠DAE=48°,
∴∠EAC=180°-∠BAC-∠DAE=27°,
∵,
∴∠C=∠EAC=27°,
故答案为:27°.
【点睛】
此题考查了平角的定义,平行线的性质:两直线平行内错角相等,熟记平行线的性质是解题的关键.
12.80
【解析】
【分析】
根据直尺的两边平行,三角板的角度和已知条件,根据平行线的性质求解即可.
【详解】
如图,
,∠1=40°,
故答案为:80
【点睛】
本题考查了三角板中角度的计算,平行线的性质,掌握平行线的性质是解题的关键.
13.##147度
【解析】
【分析】
先根据平行线的性质求出的度数,再由角平分线的定义得出的度数,根据即可得出的度数.
【详解】
解:,
,
,
.
平分,
.
,
,
.
故答案为:.
【点睛】
本题考查的是平行线的性质,熟记平行线的性质是解题的关键.
14.已知;垂直定义;等量代换;同位角相等,两直线平行;3,两直线平行,内错角相等;,两直线平行,同位角相等;等量代换;角平分线的定义
【解析】
【分析】
根据平行线的性质,平行线的判定等相关知识解答即可.
【详解】
证明:于,于(已知),
,(垂直定义).
(等量代换).
(同位角相等,两直线平行).
(两直线平行,内错角相等),
(两直线平行,同位角相等).
又(已知),
(等量代换),
平分(角平分线的定义).
故答案为:已知;垂直定义;等量代换;同位角相等,两直线平行;3,两直线平行,内错角相等;,两直线平行,同位角相等;等量代换;角平分线的定义.
【点睛】
本题考查了平行线的性质和判定,垂直即两条直角相交所成的四个角中,有一个直角;角的平分线即从角的顶点出发的射线把角分成两个相等的角,熟练掌握平行线的性质和判定是解题的关键.
15.见解析
【解析】
【分析】
根据平行线的判定与性质,求解即可.
【详解】
证明:∵,,
∴,
∴,
∵,
∴,
∴.
∴.
【点睛】
此题考查了平行线的判定与性质,解题的关键是掌握平行线的判定方法与性质.
16.(1)见解析
(2)145°
【解析】
【分析】
(1)根据ABCD,可得∠ABG=∠BGE,根据BG平分∠ABE,可得∠ABG=∠GBE,进而可得∠BGE=∠GBE;
(2)根据ABCD,可得∠ABE=∠DEF=70°,根据平角定义可得∠ABF=180° ∠ABE=110°,根据BG平分∠ABE,可得∠ABG=∠ABE=35°,进而可得∠FBG的度数.
(1)
证明:∵ABCD,
∴∠ABG=∠BGE,
∵BG平分∠ABE,
∴∠ABG=∠GBE,
∴∠BGE=∠GBE;
(2)
∵ABCD,
∴∠ABE=∠DEF=70°,
∴∠ABF=180° ∠ABE=110°,
∵BG平分∠ABE,
∴∠ABG= ∠ABE=35°,
∴∠FBG=∠ABF+∠ABG=110°+35°=145°.
答:∠FBG的度数为145°.
【点睛】
本题考查了平行线的性质,解决本题的关键是掌握平行线的性质.
17.(1)①∠EPF=∠AEP+∠CFP,理由见解析;②∠AEP+∠EPF+∠PFC=360°
(2)①130°;②∠EPF+2∠EQF=360°,理由见解析
【解析】
【分析】
(1)①过点P作,利用平行线的性质即可求解;
②过点P作,利用平行线的性质即可求解;
(2)①根据(1)的结论,结合角平分线的定义可求解;
②设:,,则可求∠P,∠Q,即可求解.
(1)
解:(1)①如图1,当点P在EF的左侧时,过点P作,则,
∴∠AEP=∠EPH,∠FPH=∠CFP,
∴∠EPF=∠EPH+∠FPH=∠AEP+∠CFP,
②当点P在EF的右侧时,过点P作,则,
∴∠AEP+∠EPM=180°,∠PFC+∠MPF=180°,
∴∠AEP+∠EPM+∠PFC+∠MPF=360°,
即,∠AEP+∠EPF+∠PFC=360°;
故答案为:∠AEP+∠EPF+∠PFC=360°;
(2)
①由(1)知∠PEA+∠PFC=∠EPF=100°,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠PFC+2∠DFQ=180°,∠PEA+2∠BEQ=180°,
故∠DFQ+∠BEQ=130°=∠EQF,
故答案为130°;
②∠EPF+2∠EQF=360°.
理由:如图3,QE,QF分别平分∠PEB和∠PFD,
设:,,
则,,
即:∠EPF+2∠EQF=360°.
【点睛】
本题主要考查了平行线的性质,平行公理和及推论、角平分线的定义以及性质等知识点,作辅助线后能求出各个角的度数,是解此题的关键..
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,AF是∠BAC的平分线, DF∥AC,若∠1=25°,则∠BDF的度数为( )
A.25° B.50° C.75° D.100°
2.如图,由ABCD,可以得到( )
A. B. C. D.
3.若要说明命题:“如果a<b,那么a2<b2”是假命题,则可以举的反例是( )
A.a=2,b=3 B.a=﹣2,b=﹣3 C.a=﹣3,b=﹣2 D.a=﹣2,b=3
4.下列命题是真命题的个数为( )
①一个角的补角大于这个角.②三角形的内角和是180°.③若,则.④相等的角是对顶角.⑤两点之间,线段最短.
A.2 B.3 C.4 D.5
5.如图,已知AB∥CD,∠1=30°,∠2=90°,则∠3等于( )
A.60° B.50° C.45° D.30°
6.如图,直线l1∥l2,∠1=136°,则∠2的度数是( )
A.44° B.46°
C.54° D.64°
7.如图,已知点B、C、D在同一直线上,,,则( )
A.42° B.45° C.48° D.无法确定
8.如图,将直尺与30°角的三角尺叠放在一起,若∠1=35°,则∠2的大小是( )
A.45° B.65° C.75° D.85°
9.如图所示,AB∥CD,若∠2=2∠1﹣6°,则∠2等于( )
A.116° B.118° C.120° D.124°
10.图书馆为将某一本书和某一个关键词建立联系,规定:当关键词出现在书中时,,否则(i,j为正整数).例如:当关键词出现在书中时,,否则.根据上述规定,某读者去图书馆寻找关键词,,,则下列相关表述错误的是( )
A.当时,只需要选择这本书就可以找到所有的关键词
B.当时,从这本书查不到需要的关键词
C.当a2j,a5j,a6j全是1时,可以从这本书查到需要的关键词
D.当时,从这本书一定查不到需要的关键词
二、填空题
11.如图,已知AE∥BC,∠BAC=105°,∠DAE=48°,则∠C=______.
12.将一把直尺与含30°的直角三角板如图摆放,使三角板的一个锐角顶点落在直尺的一边上,若∠1=40°,则∠2=_____°.
13.如图,ABCD,EFCD,平分,,则__.
14.完成下面的证明:
看图填空:已知如图,于,于,,求证:平分.
证明:于,于G(_____),
,(_____).
(_____).
(_____).
_____(_____),
_____(_____).
又(已知),
(_____),
平分(_____).
三、解答题
15.如图,已知于点F,于点D,,求证.
16.如图,ABCD,点E在直线CD上,BG平分∠ABE交CD于点G.
(1)求证:∠BGE=∠GBE;
(2)若∠DEF=70°,求∠FBG的度数.
17.如图,,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一个动点P,满足.
(1)试问:∠AEP,∠CFP,∠EPF满足怎样的数量关系?
解:由于点P是平行线AB,CD之间一动点,因此需对点P的位置进行分类讨论.
①如图1,当点P在EF的左侧时,猜想∠AEP,∠CFP,∠EPF满足的数量关系,并说明理由;
②如图2,当点P在EF的右侧时,直接写出∠AEP,∠CFP,∠EPF满足的数量关系为______.
(2)如图3,QE,QF分别平分∠PEB,∠PFD,且点P在EF左侧.
①若∠EPF=100°,则∠EQF的度数为______;
②猜想∠EPF与∠EQF的数量关系,并说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
根据两直线平行,同位角相等,可得∠FAC=∠1,再根据角平分线的定义可求得∠BAC的度数,再利用平行线的性质可求解.
【详解】
解:∵DF∥AC,
∴∠FAC=∠1=25°,
∵AF是∠BAC的平分线,
∴∠BAF=∠FAC=25°,
∴∠BAC=50°,
∵DF∥AC,
∴∠BDF=∠BAC=50°.
故选:B
【点睛】
本题主要考查了平行线的性质,角平分线的定义,熟练掌握两直线平行,同位角相等是解题的关键.
2.A
【解析】
【分析】
直接利用平行线的性质分析得出答案.
【详解】
解:,
(两直线平行,内错角相等),
故选:A.
【点睛】
此题主要考查了平行线的性质,正确把握平行线的性质是解题关键.
3.C
【解析】
【分析】
逐项进行计算,然后进行判断即可.
【详解】
解:A. a=2,b=3,有a<b, a2<b2,不符合题意;
B. a=﹣2,b=﹣3,有a>b,不符合题意;
C. a=﹣3,b=﹣2,有a<b, a2>b2,符合题意;
D. a=﹣2,b=3有a<b, a2<b2,不符合题意;
故选:C.
【点睛】
本题考查了有理数的运算和假命题的判断,解题关键是熟练进行计算,准确进行判断.
4.A
【解析】
【分析】
根据补角、三角形内角和定理、平方的计算、对顶角的性质及两点之间线段最短依次进行判断即可得出结论.
【详解】
解:①一个角的补角大于这个角,若这个角是钝角,则其补角小于这个角,错误,假命题;
②三角形的内角和是180°,正确,是真命题;
③若,则或,错误,是假命题;
④相等的角不一定是对顶角,错误,假命题;
⑤两点之间,线段最短,正确,真命题;
综上可得:②⑤是真命题,
故选:A.
【点睛】
题目主要考查命题真假的判断,理解题意,熟练掌握各个定理是解题关键.
5.A
【解析】
略
6.A
【解析】
【分析】
根据两直线平行,同位角相等求出∠1的同位角∠3的度数,再根据邻补角进行求解.
【详解】
∵直线l1∥l2,∠1=136°,
∴∠1=∠3=136°
∴∠2=180°-∠3=180°-136°=44°.
故选:A.
【点睛】
本题考查了平行线的性质,熟记性质两直线平行,同位角相等是解题的关键.
7.C
【解析】
【分析】
根据,可得,根据平行线的性质,两直线平行,内错角相等可得
【详解】
解:∵
∴
.
故选C
【点睛】
本题考查了平行线的性质与判定求角度,掌握平行线的性质与判定是解题的关键.
8.D
【解析】
【分析】
根据平角的定义和平行线的性质即可得到结论.
【详解】
解:由题意得,∠4=90°-30°=60°,
∵∠1=35°,
∴∠3=180°-60°-35°=85°,
∵AB∥CD,
∴∠3=∠2=85°,
故选:D.
【点睛】
本题考查了平行线的性质,平角的定义,熟练掌握平行线的性质是解题的关键.
9.B
【解析】
【分析】
由AB与CD平行,利用两直线平行同旁内角互补得到∠2+∠3=180°,由对顶角相等得到∠1=∠3,等量代换得到∠1=180°-∠2,再代入∠2=2∠1﹣6°,即可求出∠2的度数.
【详解】
解:如图:
∵AB∥CD,
∴∠2+∠3=180°,
∴∠3=180°-∠2,
∵∠1=∠3,
∴∠1=180°-∠2,
∴∠2=2(180°-∠2)﹣6°,
∴∠2=118°,
故选:B.
【点睛】
此题考查了对顶角性质和平行线的性质,掌握两直线平行同旁内角互补是解答此题的关键.
10.B
【解析】
【分析】
根据题意aij的值要么为1,要么为0,当关键词Ai出现在书Bj中时,元素aij=1,否则aij=0(i,j为正整数),按照此规定对每个选项分析推理即可.
【详解】
解:根据题意aij的值要么为1,要么为0,
A、a21+a51+a61=3,说明a21=1,a51=1,a61=1,故关键词“A2,A5,A6”同时出现在书B1中,
而读者去图书馆寻找书中同时有关键词“A2,A5,A6”的书,故A表述正确;
B、当a22+a52+a62<3时,则a22、a52、a62是必有值为0的,即关键词“A2,A5,A6”不同时具有,
从而不选择B2这本书,故B表述错误;
C、当a2j,a5j,a6j全是1时,则a2j=1,a5j=1,a6j=1,故关键词“A2,A5,A6”同时出现在书Bj中,
则选择Bj这本书,故C表述正确;
D、根据前述分析可知,只有当a22+a52+a62=3时,才能选择B2这本书,而a22+a52+a62的值可能为0、1、2、3,
故D表述正确.
故选:B.
【点睛】
本题考查了推理与论证,读懂题意,按照规定进行计算与推理是解题的关键.
11.27°
【解析】
【分析】
利用平角定义求出∠EAC的度数,根据,求出∠C.
【详解】
解:∵∠BAC=105°,∠DAE=48°,
∴∠EAC=180°-∠BAC-∠DAE=27°,
∵,
∴∠C=∠EAC=27°,
故答案为:27°.
【点睛】
此题考查了平角的定义,平行线的性质:两直线平行内错角相等,熟记平行线的性质是解题的关键.
12.80
【解析】
【分析】
根据直尺的两边平行,三角板的角度和已知条件,根据平行线的性质求解即可.
【详解】
如图,
,∠1=40°,
故答案为:80
【点睛】
本题考查了三角板中角度的计算,平行线的性质,掌握平行线的性质是解题的关键.
13.##147度
【解析】
【分析】
先根据平行线的性质求出的度数,再由角平分线的定义得出的度数,根据即可得出的度数.
【详解】
解:,
,
,
.
平分,
.
,
,
.
故答案为:.
【点睛】
本题考查的是平行线的性质,熟记平行线的性质是解题的关键.
14.已知;垂直定义;等量代换;同位角相等,两直线平行;3,两直线平行,内错角相等;,两直线平行,同位角相等;等量代换;角平分线的定义
【解析】
【分析】
根据平行线的性质,平行线的判定等相关知识解答即可.
【详解】
证明:于,于(已知),
,(垂直定义).
(等量代换).
(同位角相等,两直线平行).
(两直线平行,内错角相等),
(两直线平行,同位角相等).
又(已知),
(等量代换),
平分(角平分线的定义).
故答案为:已知;垂直定义;等量代换;同位角相等,两直线平行;3,两直线平行,内错角相等;,两直线平行,同位角相等;等量代换;角平分线的定义.
【点睛】
本题考查了平行线的性质和判定,垂直即两条直角相交所成的四个角中,有一个直角;角的平分线即从角的顶点出发的射线把角分成两个相等的角,熟练掌握平行线的性质和判定是解题的关键.
15.见解析
【解析】
【分析】
根据平行线的判定与性质,求解即可.
【详解】
证明:∵,,
∴,
∴,
∵,
∴,
∴.
∴.
【点睛】
此题考查了平行线的判定与性质,解题的关键是掌握平行线的判定方法与性质.
16.(1)见解析
(2)145°
【解析】
【分析】
(1)根据ABCD,可得∠ABG=∠BGE,根据BG平分∠ABE,可得∠ABG=∠GBE,进而可得∠BGE=∠GBE;
(2)根据ABCD,可得∠ABE=∠DEF=70°,根据平角定义可得∠ABF=180° ∠ABE=110°,根据BG平分∠ABE,可得∠ABG=∠ABE=35°,进而可得∠FBG的度数.
(1)
证明:∵ABCD,
∴∠ABG=∠BGE,
∵BG平分∠ABE,
∴∠ABG=∠GBE,
∴∠BGE=∠GBE;
(2)
∵ABCD,
∴∠ABE=∠DEF=70°,
∴∠ABF=180° ∠ABE=110°,
∵BG平分∠ABE,
∴∠ABG= ∠ABE=35°,
∴∠FBG=∠ABF+∠ABG=110°+35°=145°.
答:∠FBG的度数为145°.
【点睛】
本题考查了平行线的性质,解决本题的关键是掌握平行线的性质.
17.(1)①∠EPF=∠AEP+∠CFP,理由见解析;②∠AEP+∠EPF+∠PFC=360°
(2)①130°;②∠EPF+2∠EQF=360°,理由见解析
【解析】
【分析】
(1)①过点P作,利用平行线的性质即可求解;
②过点P作,利用平行线的性质即可求解;
(2)①根据(1)的结论,结合角平分线的定义可求解;
②设:,,则可求∠P,∠Q,即可求解.
(1)
解:(1)①如图1,当点P在EF的左侧时,过点P作,则,
∴∠AEP=∠EPH,∠FPH=∠CFP,
∴∠EPF=∠EPH+∠FPH=∠AEP+∠CFP,
②当点P在EF的右侧时,过点P作,则,
∴∠AEP+∠EPM=180°,∠PFC+∠MPF=180°,
∴∠AEP+∠EPM+∠PFC+∠MPF=360°,
即,∠AEP+∠EPF+∠PFC=360°;
故答案为:∠AEP+∠EPF+∠PFC=360°;
(2)
①由(1)知∠PEA+∠PFC=∠EPF=100°,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠PFC+2∠DFQ=180°,∠PEA+2∠BEQ=180°,
故∠DFQ+∠BEQ=130°=∠EQF,
故答案为130°;
②∠EPF+2∠EQF=360°.
理由:如图3,QE,QF分别平分∠PEB和∠PFD,
设:,,
则,,
即:∠EPF+2∠EQF=360°.
【点睛】
本题主要考查了平行线的性质,平行公理和及推论、角平分线的定义以及性质等知识点,作辅助线后能求出各个角的度数,是解此题的关键..
答案第1页,共2页
答案第1页,共2页
