华东师大版七年级下册数学 10.1.2 轴对称再认识 课件(共32张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 10.1.2 轴对称再认识 课件(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
数学七年级下册(华东师大版)
第10章 轴对称、平移与旋转
10.1 轴对称
第1课时 生活中的轴对称
请您欣赏:身边的数学美
发现美
请您欣赏:生活中的数学美
发现美
问题1.观察这些图形,它们有什么共同特征?
问题2.你能将上图中的图形沿某条直线折叠,
使直线两旁的部分完全重合吗?
观察想一想
探索美
探究一 轴对称图形的概念
将一张纸对折后,任意剪出一个你认为美丽的图案(折痕处不要完全剪断),然后将纸打开后铺平,观察所得到的图案,位于折痕两侧的部分有什么关系?与同伴交流.
动手做一做
探索美
小组交流:什么样的图形是轴对称图形?
归纳说一说
探索美
探索美
探索美: 轴对称图形的概念
如果一个图形沿一条直线对折,对折后的两部分
能够完全重合,这个图形就叫做轴对称图形.
折痕所在的这条直线就是对称轴.
1.下面的标志,从几何图形的角度看哪些是轴对称图形?
及时练一练
探索美:轴对称图形
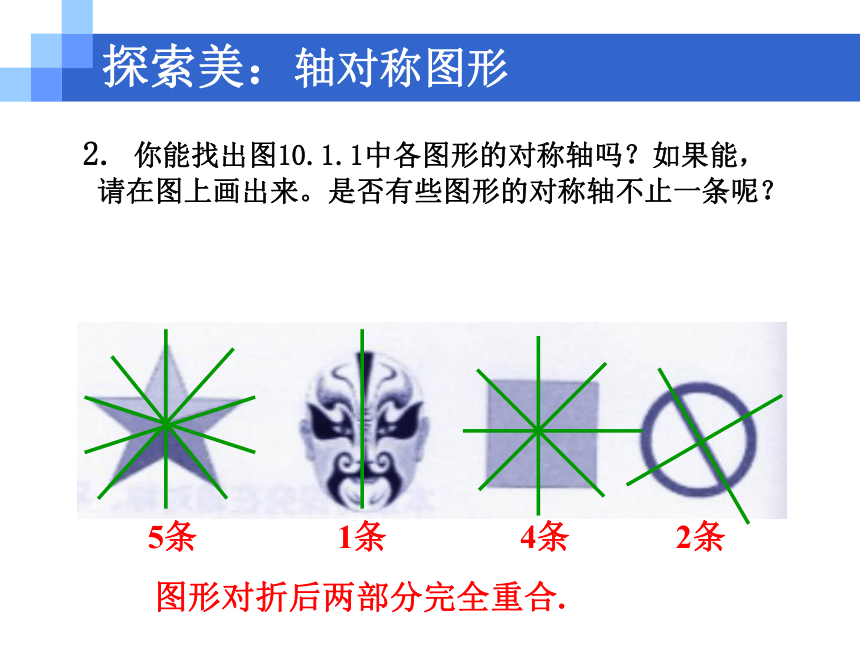
图形对折后两部分完全重合.
5条
1条
4条
2条
2. 你能找出图10.1.1中各图形的对称轴吗?如果能,
请在图上画出来。是否有些图形的对称轴不止一条呢?
探索美:轴对称图形
图形 形状 是否轴对称图形 对称轴条数
长方形
正方形
平行四边形
等腰三角形
圆形
线段
角
是
2
1
无数
1
2
是
是
是
是
4
不是
0
是
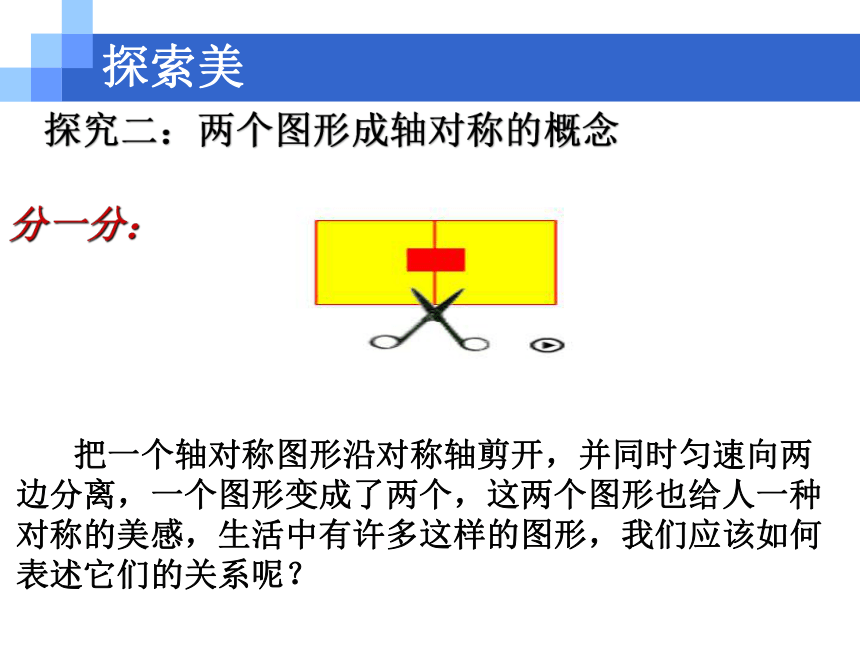
把一个轴对称图形沿对称轴剪开,并同时匀速向两边分离,一个图形变成了两个,这两个图形也给人一种对称的美感,生活中有许多这样的图形,我们应该如何表述它们的关系呢?
探索美
分一分:
分一分:
把一个图形沿着某条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形成轴对称.
这条直线叫做对称轴.
折叠后重合的点是对应点,叫做对称点.
探索美:两个图形成轴对称的概念
A1
C1
B1
图1沿直线m折叠后可与图2重合
1.确定 A、B、C 三点的对称点A1、B1、 C1
2.讨论AC与A1C1之间的关系,∠ACB与∠ A1C1B1的大小。
1
2
m
探索美
思考:
根据你对轴对称的理解,你能发现轴对称有哪些基本特征?
探索美
基本特征:
轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的,所以轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
探索美
2cm
55°
如图,△ABC与△DEF关于直线a对称,
若AB=2cm,∠C=55°,则DE= ,∠F= 。
练习反馈
探索美
议一议:
问题1:轴对称图形与两个图形成轴对称有什么区别?
问题2:如果把两个成轴对称的图形看成一个整体,它
是一个轴对称图形吗?
探索美
轴对称图形
成轴对称
一分为二
合二为一
探索美
轴对称图形 两个图形成轴对称
区别 一个图形(具有特殊形状) 两个图形(具有特殊位置关系)
对称轴( )
与位置无关
对称轴 ( )
与位置有关
联系 1.沿着某条直线对折后,直线两旁的部分都能完全重合.
2.如果把一个轴对称图形沿对称轴分成两个图形,那么这 两个图形关于这条直线对称;如果把两个成轴对称的图形看成一个图形,那么这个图形就是轴对称图形.
探究三:轴对称图形与两个图形成轴对称的区别和联系
探索美
至少一条
只有一条
(1)下图整个图形是轴对称图形吗?如果是,请指出它的对称轴.
(3)在下图中任选一个三角形,你能指出它分别与哪个三角形成轴对称吗?
(2)下图可以看作某两个图形成轴对称吗?
练一练
探索美
1.(嘉兴)下列图形中,轴对称图形
是( )
(A)
B
2.下列图形中对称轴最多的是( )
A.长方形 B.正方形
C.圆 D.五角星
c
应用
3.下面哪一个选项的右边图形与左边图形成轴对称?
C
应用
优美的自然风光及倒影
天安门
北京天坛
大 众
雪 铁 龙
奔 驰
丰 田
汽 车 标 志
实物图案
课堂小结
数学源于生活,对称之美一直在我们身边,并且给我们带来丰富多彩的视觉享受。
让我们走出去,
发现身边的!美
!
2、收集生活中具有轴对称图形特征的
图片与物体,和同学一起欣赏交流。
3、用圆规画出多个大小不一的圆,剪下来,
拼一拼,看看能拼出多少种轴对称图形,并画出他们的对称轴。
课后作业:
1、课本P100,练习1,2
数学七年级下册(华东师大版)
第10章 轴对称、平移与旋转
10.1 轴对称
第1课时 生活中的轴对称
请您欣赏:身边的数学美
发现美
请您欣赏:生活中的数学美
发现美
问题1.观察这些图形,它们有什么共同特征?
问题2.你能将上图中的图形沿某条直线折叠,
使直线两旁的部分完全重合吗?
观察想一想
探索美
探究一 轴对称图形的概念
将一张纸对折后,任意剪出一个你认为美丽的图案(折痕处不要完全剪断),然后将纸打开后铺平,观察所得到的图案,位于折痕两侧的部分有什么关系?与同伴交流.
动手做一做
探索美
小组交流:什么样的图形是轴对称图形?
归纳说一说
探索美
探索美
探索美: 轴对称图形的概念
如果一个图形沿一条直线对折,对折后的两部分
能够完全重合,这个图形就叫做轴对称图形.
折痕所在的这条直线就是对称轴.
1.下面的标志,从几何图形的角度看哪些是轴对称图形?
及时练一练
探索美:轴对称图形
图形对折后两部分完全重合.
5条
1条
4条
2条
2. 你能找出图10.1.1中各图形的对称轴吗?如果能,
请在图上画出来。是否有些图形的对称轴不止一条呢?
探索美:轴对称图形
图形 形状 是否轴对称图形 对称轴条数
长方形
正方形
平行四边形
等腰三角形
圆形
线段
角
是
2
1
无数
1
2
是
是
是
是
4
不是
0
是
把一个轴对称图形沿对称轴剪开,并同时匀速向两边分离,一个图形变成了两个,这两个图形也给人一种对称的美感,生活中有许多这样的图形,我们应该如何表述它们的关系呢?
探索美
分一分:
分一分:
把一个图形沿着某条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形成轴对称.
这条直线叫做对称轴.
折叠后重合的点是对应点,叫做对称点.
探索美:两个图形成轴对称的概念
A1
C1
B1
图1沿直线m折叠后可与图2重合
1.确定 A、B、C 三点的对称点A1、B1、 C1
2.讨论AC与A1C1之间的关系,∠ACB与∠ A1C1B1的大小。
1
2
m
探索美
思考:
根据你对轴对称的理解,你能发现轴对称有哪些基本特征?
探索美
基本特征:
轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的,所以轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
探索美
2cm
55°
如图,△ABC与△DEF关于直线a对称,
若AB=2cm,∠C=55°,则DE= ,∠F= 。
练习反馈
探索美
议一议:
问题1:轴对称图形与两个图形成轴对称有什么区别?
问题2:如果把两个成轴对称的图形看成一个整体,它
是一个轴对称图形吗?
探索美
轴对称图形
成轴对称
一分为二
合二为一
探索美
轴对称图形 两个图形成轴对称
区别 一个图形(具有特殊形状) 两个图形(具有特殊位置关系)
对称轴( )
与位置无关
对称轴 ( )
与位置有关
联系 1.沿着某条直线对折后,直线两旁的部分都能完全重合.
2.如果把一个轴对称图形沿对称轴分成两个图形,那么这 两个图形关于这条直线对称;如果把两个成轴对称的图形看成一个图形,那么这个图形就是轴对称图形.
探究三:轴对称图形与两个图形成轴对称的区别和联系
探索美
至少一条
只有一条
(1)下图整个图形是轴对称图形吗?如果是,请指出它的对称轴.
(3)在下图中任选一个三角形,你能指出它分别与哪个三角形成轴对称吗?
(2)下图可以看作某两个图形成轴对称吗?
练一练
探索美
1.(嘉兴)下列图形中,轴对称图形
是( )
(A)
B
2.下列图形中对称轴最多的是( )
A.长方形 B.正方形
C.圆 D.五角星
c
应用
3.下面哪一个选项的右边图形与左边图形成轴对称?
C
应用
优美的自然风光及倒影
天安门
北京天坛
大 众
雪 铁 龙
奔 驰
丰 田
汽 车 标 志
实物图案
课堂小结
数学源于生活,对称之美一直在我们身边,并且给我们带来丰富多彩的视觉享受。
让我们走出去,
发现身边的!美
!
2、收集生活中具有轴对称图形特征的
图片与物体,和同学一起欣赏交流。
3、用圆规画出多个大小不一的圆,剪下来,
拼一拼,看看能拼出多少种轴对称图形,并画出他们的对称轴。
课后作业:
1、课本P100,练习1,2
