2.4 单摆 同步练习题(Word版含答案)
文档属性
| 名称 | 2.4 单摆 同步练习题(Word版含答案) | 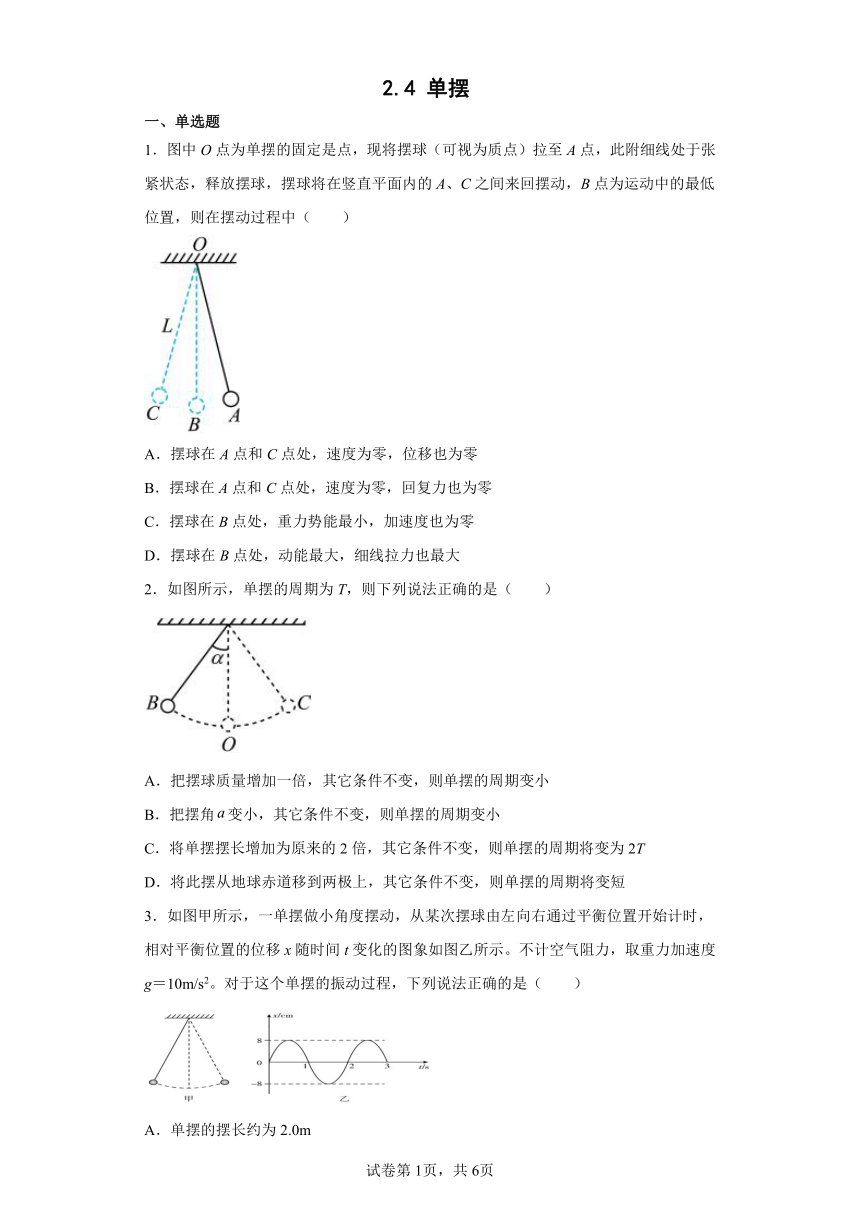 | |
| 格式 | doc | ||
| 文件大小 | 424.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-24 22:32:45 | ||
图片预览





文档简介
2.4 单摆
一、单选题
1.图中O点为单摆的固定是点,现将摆球(可视为质点)拉至A点,此附细线处于张紧状态,释放摆球,摆球将在竖直平面内的A、C之间来回摆动,B点为运动中的最低位置,则在摆动过程中( )
A.摆球在A点和C点处,速度为零,位移也为零
B.摆球在A点和C点处,速度为零,回复力也为零
C.摆球在B点处,重力势能最小,加速度也为零
D.摆球在B点处,动能最大,细线拉力也最大
2.如图所示,单摆的周期为T,则下列说法正确的是( )
A.把摆球质量增加一倍,其它条件不变,则单摆的周期变小
B.把摆角变小,其它条件不变,则单摆的周期变小
C.将单摆摆长增加为原来的2倍,其它条件不变,则单摆的周期将变为2T
D.将此摆从地球赤道移到两极上,其它条件不变,则单摆的周期将变短
3.如图甲所示,一单摆做小角度摆动,从某次摆球由左向右通过平衡位置开始计时,相对平衡位置的位移x随时间t变化的图象如图乙所示。不计空气阻力,取重力加速度g=10m/s2。对于这个单摆的振动过程,下列说法正确的是( )
A.单摆的摆长约为2.0m
B.单摆的位移x随时间t变化的关系式为x=8cosπt(cm)
C.从t=0.5s到t=1.0s的过程中,摆球的重力势能逐渐增大
D.从t=1.0s到t=1.5s的过程中,摆球所受回复力逐渐增大
4.一单摆做小角度摆动,其振动图像如图所示,以下说法正确的是( )
A.t1时刻摆球的速度最大,悬线对它的拉力最小
B.t2时刻摆球的速度为零,悬线对它的拉力最小
C.t3时刻摆球的速度最大,悬线对它的拉力最大
D.t4时刻摆球的速度最大,悬线对它的拉力最大
5.惠更斯利用摆的等时性原理制成了第一座摆钟。如图甲所示为日常生活中我们能见到的一种摆钟,图乙为摆钟的结构示意图,圆盘固定在摆杆上,螺母可以沿摆杆上下移动。在黄山山脚走时准确的摆钟移到黄山山顶(未做其他调整),摆钟摆动变慢了,下列说法正确的是( )
A.黄山山顶的重力加速度较小,若要调准摆钟可将螺母适当向下移动
B.黄山山顶的重力加速度较小,若要调准摆钟可将螺母适当向上移动
C.黄山山顶的重力加速度较大,若要调准摆钟可将螺母适当向下移动
D.黄山山顶的重力加速度较大,若要调准摆钟可将螺母适当向上移动
6.如图所示,倾角为的斜面上的B点固定一光滑圆弧槽(对应的圆心角小于),其圆心在B点正上方的O点,另外,光滑斜面和的下端亦在上,让可视为质点的小球分别无初速出发,从A点到达B的时间为,从O点到达C的时间为,从O点到达D的时间为。比较这三段时间,正确的是( )
A. B. C. D.
二、多选题
7.单摆在两点之间做简谐运动,点为平衡位置,如图甲所示,单摆的振动图像如图乙所示(向右为正方向),取重力加速度大小,下列说法正确的是( )
A.单摆的振幅为 B.单摆的摆动频率为
C.时,摆球在点 D.单摆的摆长为
8.固定光滑圆弧面上有一个小球,将它从最低点移开一小段距离,时刻将小球由静止释放,小球以最低点为平衡位置左右振动。已知圆弧半径,当地的重力加速度大小,,下列哪些时刻小球运动到最低点( )
A.0.5s B.1s C.1.5s D.2s
9.单摆做简谐运动时( )
A.不同的摆,摆长大的,周期大
B.不同的摆,摆球质量大的,周期大
C.相同的摆,振动能量由振幅决定
D.相同的摆,振动能量也相同
10.如图所示为同一地点两单摆甲、乙的振动图象,则下列说法正确的是( )
A.甲摆的振幅比乙摆振幅大
B.甲摆的机械能比乙摆的大
C.甲、乙两单摆的摆长相等
D.由图象可以求出当地的重力加速度
E.在t=1.0s时刻乙摆具有最大速度
三、填空题
11.中国载人登月工程计划在2030年前后实现航天员登月。已知月球表面重力加速度是地球表面重力加速度的,航天员若将地球上的单摆带到月球上去,此单摆的周期会变为原来的______倍。
12.某同学利用计算机绘制了a、b两个摆球的振动图像如图所示,由图可知,两单摆摆长之比______。在时,b球相对平衡位置的位移是______。
13.一个理想的单摆,已知其周期为T。如果由于某种原因重力加速度变为原来的2倍,振幅变为原来的3倍,摆长变为原来的8倍,摆球质量变为原来的2倍,它的周期变为___________。
14.有甲、乙两个单摆,在同一地点、同一时间内甲摆摆动35次,乙摆摆动21次,如甲摆的摆长是45cm,则乙摆的摆长是______。
四、解答题
15.如图所示为一个双线摆,由挂在水平天花板上两根等长的细绳悬挂一个小球组成,绳长均为L,细绳与天花板成角,当地重力加速度为g,当小球垂直纸面做简谐振动时,求振动N次所需时间。不计摆球的直径。
16. 秋千由踏板和绳构成,人在秋千上的摆动过程可以简化为单摆的摆动,等效“摆球”的质量为m,人蹲在踏板上时摆长为,人站立时摆长为。不计空气阻力,重力加速度大小为g 。
(1)如果摆长为,“摆球”摆到最高点时摆角为θ,求此时“摆球”加速度的大小。
(2)人蹲着摆动和站立摆动时如果摆角均小于5°,则时间t内哪一种情况摆动次数多?多几次?
(3)在没有别人帮助的情况下,人可以通过在低处站起、在高处蹲下的方式使“摆球”摆得越来越高。设人蹲在踏板上从最大摆角开始运动,到最低点时突然站起,此后保持站立姿势摆到另一边的最大摆角为。假定人在最低点站起前后“摆球”摆动速度大小不变,通过计算证明。
17.如图,将一倾角为的斜面体(斜面光滑且足够长)固定在水平地面上,一劲度系数为、自然长度为的轻弹簧的上端固定在斜面上,下端与质量为的小滑块连接且弹簧与斜面平行。用外力控制小滑块使弹簧压缩了时将小滑块由静止开始释放,重力加速度为g。
(1) 求小滑块做简谐运动的振幅A;
(2) 若沿斜面向下为正方向且小滑块在斜面上简谐运动的周期为,小滑块沿斜面向下运动经过平衡位置时开始计时,请写出小滑块振动过程中位移随时间变化的函数关系式。
(3) 求小滑块的最大加速度am和弹簧的最大长度Lm。
18.有一单摆,在地球表面的周期为2s,已知月球表面的重力加速度约为地球表面重力加速度的。(取,结果均保留2位有效数字)
(1)将该单摆置于月球表面,其周期为多大?
(2)该单摆的摆长为多少?
试卷第1页,共3页
试卷第6页,共6页
参考答案:
1.D
【解析】
【分析】
【详解】
AB.摆球在摆动过程中,最高点C处是摆球的最大位移位置,速度为零,回复力最大,故AB错误;
CD.在最低点B,是摆球的平衡位置,速度最大,动能最大,重力势能最小,摆球做圆周运动,绳的拉力最大,加速度不为零,故C错误、D正确。
故选D。
2.D
【解析】
【分析】
【详解】
ABC.根据单摆周期公式
可知,周期与摆角和摆球的质量无关,摆长增加为原来的2倍,其它条件不变,则单摆的周期将变为倍,故ABC错误;
D.地球两极的重力加速度大于赤道的重力加速度,根据
可得将此摆从地球赤道移到两极上,其它条件不变,则单摆的周期将变短,故D正确。
故选D。
3.D
【解析】
【分析】
【详解】
A.由图乙可知,单摆周期为2s,由单摆周期公式
可解得单摆的摆长为
A错误;
B.单摆的位移x随时间t变化的关系式为
B错误;
C.从t=0.5s到t=1.0s的过程中,摆球从最高点回到平衡位置,摆球的重力势能逐渐减小,C错误;
D.从t=1.0s到t=1.5s的过程中,摆球从平衡位置回到最高点,位移逐渐增大,回复力与位移成正比,古摆球所受回复力逐渐增大,D正确。
故选D。
4.D
【解析】
【详解】
AC.由题图可知,在t1时刻和t3时刻摆球的位移最大,回复力最大,速度为零,悬线的拉力最小,故AC错误;
BD.在t2时刻和t4时刻摆球在平衡位置,速度最大,悬线的拉力最大,回复力为零,故B错误,D正确。
故选D。
5.B
【解析】
【详解】
由题意可知摆钟由黄山山脚移到黄山山顶时周期变大,根据单摆周期公式
T=2π
可知山顶的重力加速度较小,为调准摆钟,使摆钟的周期适当变短,需要适当增大摆长,应将螺母适当向上移动。
故选B。
6.A
【解析】
【详解】
由单摆运动的等时性可知从A点到达B的时间
由于OD垂直于MN,则点D同样位于AB所构成的圆上,分析可知OD与竖直方向夹角为倾角,则OD段为
解得
同理利用等时圆分析可知小于,故A正确,BCD错误。
故选A。
7.BC
【解析】
【详解】
A.由图乙可知单摆的振幅为4cm,故A错误;
B.单摆的摆动频率为
故B正确;
C.由单摆的周期性可知,时和摆球的运动状态相同,可知摆球在点,故C正确;
D.由单摆的周期公式
代入数据解得
故D错误。
故选BC。
8.AC
【解析】
【详解】
小球运动可等效为单摆,摆动周期
小球从左侧最大位移处释放,在,n=0,1,2,3,…的时刻经过最低点,所以0.5s和1.5s时小球均经过最低点,故BD错误,AC选项正确。
故选AC。
9.AC
【解析】
【分析】
【详解】
A.根据单摆的周期公式
可知,不同的摆,摆长大的,周期大,所以A正确;
B.根据单摆的周期公式
可知,单摆的周期与摆球的质量无关,所以B错误;
CD.相同的摆,振动能量由振幅决定,振幅越大振动能量越大,所以C正确;D错误;
故选AC。
10.ACE
【解析】
【详解】
A.甲摆的振幅为10 cm,乙摆的振幅为7 cm,则甲摆的振幅比乙摆大,故A正确;
B.虽然甲摆的振幅比乙摆大,但由于两单摆的质量未知,所以无法比较机械能的大小,故B错误;
C.由题图看出,两单摆的周期相同,同一地点g相同,由单摆的周期公式
T=2π
知甲、乙两单摆的摆长l相等,故C正确;
D.由单摆的周期公式
得
由于单摆的摆长不知道,所以不能求得当地的重力加速度,故D错误;
E.在t=1.0s时刻乙摆经过平衡位置,具有最大速度,故E正确。
故选ACE。
11.
【解析】
【详解】
依题意,根据单摆周期公式
可得
所以,此单摆的周期会变为原来的倍。
12. 或
【解析】
【详解】
周期等于完成一次全振动的时间,由图可知,a、b两单摆的周期之比为2:3,根据
得
因为a、b的周期之比为2:3,则摆长之比为4:9
由图可知,b摆球的振幅
,
则
可得b的振动方程
所以当时,b球相对平衡位置的位移是
13.2T
14.125
【解析】
【详解】
甲、乙两个单摆,在同一地点、同一时间内甲摆摆动35次,乙摆摆动21次,由单摆周期公式可知
甲摆的摆长是45cm,则乙摆的摆长是125cm。
15.
【解析】
【详解】
如图所示,小球在摆动时,等效摆长为
l=Lsinα
由于小球做简谐运动,由单摆的振动周期为
振动N次所需时间为
16.(1)a=gsinθ;(2)站着摆动时振动次数多;Δn =;(3)见解析
【解析】
【详解】
(1)在最高点时受力如图
此时加速度垂直于摆线沿轨迹切线方向, 由牛顿第二定律:
mgsinθ=ma
所以
a=gsinθ
(2)摆角小于5°,单摆做简谐振动,周期
所以蹲着摆动时t时间内振动次数
站着摆动时t时间内振动次数
因为l1>l2,所以站着摆动时振动次数多。
多了次数
(3)设人在最低点站起前后“摆球”的摆动速度大小为v,根据功能关系(或机械能守恒) 人蹲在踏板上从最大摆角开始运动到最低点的过程中,有
保持站立姿势摆到另一边的最大摆角为的过程中,有:
由此可得
因为l1>l2,得
所以
17.(1);(2);(3),
【解析】
【详解】
(1)平衡位置时
解得
小滑块做简谐运动的振幅为
(2)角速度
位移随时间变化的函数关系式为
(3)由牛顿第二定律得
解得
由简谐运动的对称性可知,弹簧的最大长度为
18.1)4.9s或2s;(2)0.99m
【解析】
【详解】
(1)由单摆的周期公式知
所以
则
(或)
(2)根据周期公式知
答案第1页,共2页
答案第10页,共1页
一、单选题
1.图中O点为单摆的固定是点,现将摆球(可视为质点)拉至A点,此附细线处于张紧状态,释放摆球,摆球将在竖直平面内的A、C之间来回摆动,B点为运动中的最低位置,则在摆动过程中( )
A.摆球在A点和C点处,速度为零,位移也为零
B.摆球在A点和C点处,速度为零,回复力也为零
C.摆球在B点处,重力势能最小,加速度也为零
D.摆球在B点处,动能最大,细线拉力也最大
2.如图所示,单摆的周期为T,则下列说法正确的是( )
A.把摆球质量增加一倍,其它条件不变,则单摆的周期变小
B.把摆角变小,其它条件不变,则单摆的周期变小
C.将单摆摆长增加为原来的2倍,其它条件不变,则单摆的周期将变为2T
D.将此摆从地球赤道移到两极上,其它条件不变,则单摆的周期将变短
3.如图甲所示,一单摆做小角度摆动,从某次摆球由左向右通过平衡位置开始计时,相对平衡位置的位移x随时间t变化的图象如图乙所示。不计空气阻力,取重力加速度g=10m/s2。对于这个单摆的振动过程,下列说法正确的是( )
A.单摆的摆长约为2.0m
B.单摆的位移x随时间t变化的关系式为x=8cosπt(cm)
C.从t=0.5s到t=1.0s的过程中,摆球的重力势能逐渐增大
D.从t=1.0s到t=1.5s的过程中,摆球所受回复力逐渐增大
4.一单摆做小角度摆动,其振动图像如图所示,以下说法正确的是( )
A.t1时刻摆球的速度最大,悬线对它的拉力最小
B.t2时刻摆球的速度为零,悬线对它的拉力最小
C.t3时刻摆球的速度最大,悬线对它的拉力最大
D.t4时刻摆球的速度最大,悬线对它的拉力最大
5.惠更斯利用摆的等时性原理制成了第一座摆钟。如图甲所示为日常生活中我们能见到的一种摆钟,图乙为摆钟的结构示意图,圆盘固定在摆杆上,螺母可以沿摆杆上下移动。在黄山山脚走时准确的摆钟移到黄山山顶(未做其他调整),摆钟摆动变慢了,下列说法正确的是( )
A.黄山山顶的重力加速度较小,若要调准摆钟可将螺母适当向下移动
B.黄山山顶的重力加速度较小,若要调准摆钟可将螺母适当向上移动
C.黄山山顶的重力加速度较大,若要调准摆钟可将螺母适当向下移动
D.黄山山顶的重力加速度较大,若要调准摆钟可将螺母适当向上移动
6.如图所示,倾角为的斜面上的B点固定一光滑圆弧槽(对应的圆心角小于),其圆心在B点正上方的O点,另外,光滑斜面和的下端亦在上,让可视为质点的小球分别无初速出发,从A点到达B的时间为,从O点到达C的时间为,从O点到达D的时间为。比较这三段时间,正确的是( )
A. B. C. D.
二、多选题
7.单摆在两点之间做简谐运动,点为平衡位置,如图甲所示,单摆的振动图像如图乙所示(向右为正方向),取重力加速度大小,下列说法正确的是( )
A.单摆的振幅为 B.单摆的摆动频率为
C.时,摆球在点 D.单摆的摆长为
8.固定光滑圆弧面上有一个小球,将它从最低点移开一小段距离,时刻将小球由静止释放,小球以最低点为平衡位置左右振动。已知圆弧半径,当地的重力加速度大小,,下列哪些时刻小球运动到最低点( )
A.0.5s B.1s C.1.5s D.2s
9.单摆做简谐运动时( )
A.不同的摆,摆长大的,周期大
B.不同的摆,摆球质量大的,周期大
C.相同的摆,振动能量由振幅决定
D.相同的摆,振动能量也相同
10.如图所示为同一地点两单摆甲、乙的振动图象,则下列说法正确的是( )
A.甲摆的振幅比乙摆振幅大
B.甲摆的机械能比乙摆的大
C.甲、乙两单摆的摆长相等
D.由图象可以求出当地的重力加速度
E.在t=1.0s时刻乙摆具有最大速度
三、填空题
11.中国载人登月工程计划在2030年前后实现航天员登月。已知月球表面重力加速度是地球表面重力加速度的,航天员若将地球上的单摆带到月球上去,此单摆的周期会变为原来的______倍。
12.某同学利用计算机绘制了a、b两个摆球的振动图像如图所示,由图可知,两单摆摆长之比______。在时,b球相对平衡位置的位移是______。
13.一个理想的单摆,已知其周期为T。如果由于某种原因重力加速度变为原来的2倍,振幅变为原来的3倍,摆长变为原来的8倍,摆球质量变为原来的2倍,它的周期变为___________。
14.有甲、乙两个单摆,在同一地点、同一时间内甲摆摆动35次,乙摆摆动21次,如甲摆的摆长是45cm,则乙摆的摆长是______。
四、解答题
15.如图所示为一个双线摆,由挂在水平天花板上两根等长的细绳悬挂一个小球组成,绳长均为L,细绳与天花板成角,当地重力加速度为g,当小球垂直纸面做简谐振动时,求振动N次所需时间。不计摆球的直径。
16. 秋千由踏板和绳构成,人在秋千上的摆动过程可以简化为单摆的摆动,等效“摆球”的质量为m,人蹲在踏板上时摆长为,人站立时摆长为。不计空气阻力,重力加速度大小为g 。
(1)如果摆长为,“摆球”摆到最高点时摆角为θ,求此时“摆球”加速度的大小。
(2)人蹲着摆动和站立摆动时如果摆角均小于5°,则时间t内哪一种情况摆动次数多?多几次?
(3)在没有别人帮助的情况下,人可以通过在低处站起、在高处蹲下的方式使“摆球”摆得越来越高。设人蹲在踏板上从最大摆角开始运动,到最低点时突然站起,此后保持站立姿势摆到另一边的最大摆角为。假定人在最低点站起前后“摆球”摆动速度大小不变,通过计算证明。
17.如图,将一倾角为的斜面体(斜面光滑且足够长)固定在水平地面上,一劲度系数为、自然长度为的轻弹簧的上端固定在斜面上,下端与质量为的小滑块连接且弹簧与斜面平行。用外力控制小滑块使弹簧压缩了时将小滑块由静止开始释放,重力加速度为g。
(1) 求小滑块做简谐运动的振幅A;
(2) 若沿斜面向下为正方向且小滑块在斜面上简谐运动的周期为,小滑块沿斜面向下运动经过平衡位置时开始计时,请写出小滑块振动过程中位移随时间变化的函数关系式。
(3) 求小滑块的最大加速度am和弹簧的最大长度Lm。
18.有一单摆,在地球表面的周期为2s,已知月球表面的重力加速度约为地球表面重力加速度的。(取,结果均保留2位有效数字)
(1)将该单摆置于月球表面,其周期为多大?
(2)该单摆的摆长为多少?
试卷第1页,共3页
试卷第6页,共6页
参考答案:
1.D
【解析】
【分析】
【详解】
AB.摆球在摆动过程中,最高点C处是摆球的最大位移位置,速度为零,回复力最大,故AB错误;
CD.在最低点B,是摆球的平衡位置,速度最大,动能最大,重力势能最小,摆球做圆周运动,绳的拉力最大,加速度不为零,故C错误、D正确。
故选D。
2.D
【解析】
【分析】
【详解】
ABC.根据单摆周期公式
可知,周期与摆角和摆球的质量无关,摆长增加为原来的2倍,其它条件不变,则单摆的周期将变为倍,故ABC错误;
D.地球两极的重力加速度大于赤道的重力加速度,根据
可得将此摆从地球赤道移到两极上,其它条件不变,则单摆的周期将变短,故D正确。
故选D。
3.D
【解析】
【分析】
【详解】
A.由图乙可知,单摆周期为2s,由单摆周期公式
可解得单摆的摆长为
A错误;
B.单摆的位移x随时间t变化的关系式为
B错误;
C.从t=0.5s到t=1.0s的过程中,摆球从最高点回到平衡位置,摆球的重力势能逐渐减小,C错误;
D.从t=1.0s到t=1.5s的过程中,摆球从平衡位置回到最高点,位移逐渐增大,回复力与位移成正比,古摆球所受回复力逐渐增大,D正确。
故选D。
4.D
【解析】
【详解】
AC.由题图可知,在t1时刻和t3时刻摆球的位移最大,回复力最大,速度为零,悬线的拉力最小,故AC错误;
BD.在t2时刻和t4时刻摆球在平衡位置,速度最大,悬线的拉力最大,回复力为零,故B错误,D正确。
故选D。
5.B
【解析】
【详解】
由题意可知摆钟由黄山山脚移到黄山山顶时周期变大,根据单摆周期公式
T=2π
可知山顶的重力加速度较小,为调准摆钟,使摆钟的周期适当变短,需要适当增大摆长,应将螺母适当向上移动。
故选B。
6.A
【解析】
【详解】
由单摆运动的等时性可知从A点到达B的时间
由于OD垂直于MN,则点D同样位于AB所构成的圆上,分析可知OD与竖直方向夹角为倾角,则OD段为
解得
同理利用等时圆分析可知小于,故A正确,BCD错误。
故选A。
7.BC
【解析】
【详解】
A.由图乙可知单摆的振幅为4cm,故A错误;
B.单摆的摆动频率为
故B正确;
C.由单摆的周期性可知,时和摆球的运动状态相同,可知摆球在点,故C正确;
D.由单摆的周期公式
代入数据解得
故D错误。
故选BC。
8.AC
【解析】
【详解】
小球运动可等效为单摆,摆动周期
小球从左侧最大位移处释放,在,n=0,1,2,3,…的时刻经过最低点,所以0.5s和1.5s时小球均经过最低点,故BD错误,AC选项正确。
故选AC。
9.AC
【解析】
【分析】
【详解】
A.根据单摆的周期公式
可知,不同的摆,摆长大的,周期大,所以A正确;
B.根据单摆的周期公式
可知,单摆的周期与摆球的质量无关,所以B错误;
CD.相同的摆,振动能量由振幅决定,振幅越大振动能量越大,所以C正确;D错误;
故选AC。
10.ACE
【解析】
【详解】
A.甲摆的振幅为10 cm,乙摆的振幅为7 cm,则甲摆的振幅比乙摆大,故A正确;
B.虽然甲摆的振幅比乙摆大,但由于两单摆的质量未知,所以无法比较机械能的大小,故B错误;
C.由题图看出,两单摆的周期相同,同一地点g相同,由单摆的周期公式
T=2π
知甲、乙两单摆的摆长l相等,故C正确;
D.由单摆的周期公式
得
由于单摆的摆长不知道,所以不能求得当地的重力加速度,故D错误;
E.在t=1.0s时刻乙摆经过平衡位置,具有最大速度,故E正确。
故选ACE。
11.
【解析】
【详解】
依题意,根据单摆周期公式
可得
所以,此单摆的周期会变为原来的倍。
12. 或
【解析】
【详解】
周期等于完成一次全振动的时间,由图可知,a、b两单摆的周期之比为2:3,根据
得
因为a、b的周期之比为2:3,则摆长之比为4:9
由图可知,b摆球的振幅
,
则
可得b的振动方程
所以当时,b球相对平衡位置的位移是
13.2T
14.125
【解析】
【详解】
甲、乙两个单摆,在同一地点、同一时间内甲摆摆动35次,乙摆摆动21次,由单摆周期公式可知
甲摆的摆长是45cm,则乙摆的摆长是125cm。
15.
【解析】
【详解】
如图所示,小球在摆动时,等效摆长为
l=Lsinα
由于小球做简谐运动,由单摆的振动周期为
振动N次所需时间为
16.(1)a=gsinθ;(2)站着摆动时振动次数多;Δn =;(3)见解析
【解析】
【详解】
(1)在最高点时受力如图
此时加速度垂直于摆线沿轨迹切线方向, 由牛顿第二定律:
mgsinθ=ma
所以
a=gsinθ
(2)摆角小于5°,单摆做简谐振动,周期
所以蹲着摆动时t时间内振动次数
站着摆动时t时间内振动次数
因为l1>l2,所以站着摆动时振动次数多。
多了次数
(3)设人在最低点站起前后“摆球”的摆动速度大小为v,根据功能关系(或机械能守恒) 人蹲在踏板上从最大摆角开始运动到最低点的过程中,有
保持站立姿势摆到另一边的最大摆角为的过程中,有:
由此可得
因为l1>l2,得
所以
17.(1);(2);(3),
【解析】
【详解】
(1)平衡位置时
解得
小滑块做简谐运动的振幅为
(2)角速度
位移随时间变化的函数关系式为
(3)由牛顿第二定律得
解得
由简谐运动的对称性可知,弹簧的最大长度为
18.1)4.9s或2s;(2)0.99m
【解析】
【详解】
(1)由单摆的周期公式知
所以
则
(或)
(2)根据周期公式知
答案第1页,共2页
答案第10页,共1页
