人教版三年级下册数学第八单元测试卷(含答案)
文档属性
| 名称 | 人教版三年级下册数学第八单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 188.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 07:36:19 | ||
图片预览




文档简介
第八单元测试卷(含答案)
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 六 总分
得分
一、填空题(共36分)
1.(本题4分)从2、7、0、5中任取三个数字,可以组成( )个不同的三位数,在这些三位数中,最大的是( )。
2.(本题4分)数字3、7、5共可以组成( )个不同的三位数,其中最大数比最小数多( )。
3.(本题3分)用6,5,2,1四张卡片能组成的最大三位数是( ),能组成的最小三位数是( ),它们相差( )。
4.(本题3分)唐僧师徒四人排成一排照相,如果最左边的猪八戒站着不动,其他三人可以任意调换位置,一共有( )种站法。
5.(本题3分)6名同学进行象棋比赛,如果每两人赛一场,一共要赛( )场。
6.(本题3分)有5个城市,每两个城市之间修一条高速公路,可以修( ) 条高速公路。
7.(本题4分)用5、7和6这三个数字可以写出( )个没有重复的两位小数,其中最大的是( )。
8.(本题3分)运动会上,301班何一、沈倩、王晓、刘丽将参加女子组4×100米接力赛,何一跑得最快,体育老师已经将她排在第一棒。这四名同学跑接力赛一共有( )种排法。
9.(本题3分)现有1克、2克、5克的砝码各一个(砝码只能放在右盘),在天平上最多能称出( )种不同的质量。
10.(本题3分)班级图书角有3本故事书,2本科技书。李刚两种书各借一本,有( )种不同的选择方法。
11.(本题3分)从3、4、5这三个数中,任意选其中两个数组成乘法算式,有________种不同的积。
二、判断题(共8分)
12.(本题2分)有5道不同的计算题,小明任意选4道做,共有20种不同选法。( )
13.(本题2分)5人中每2人通一次电话,一共要通10次电话。( )
14.(本题2分)李老师要从甲、乙、丙、丁中选出1名班长和1名副班长,共有14种不同的选法。( )
15.(本题2分)5个身高各不相同的同学按从高到矮的顺序排列,只能有1种排法.。( )
三、选择题(共12分)
16.(本题2分)明明、红红、丽丽、君君在元旦前互赠1张贺卡,一共需要( )张贺卡。
A.4 B.12 C.16
17.(本题2分)用3、0、5、7能组成( )个没有重复数字的两位数。
A.6 B.9 C.12
18.(本题2分)小明有5元和2元面值的人民币各6张,如果要买一个30元的书包,有几种恰好付给30元的方式?( )
A.4种 B.3种 C.2种
19.(本题2分)下图有几个长方形?( )
A.5个 B.8个 C.9个
20.(本题2分)兰兰有两件上衣、三条裤子,每次上装和下装各穿一件,一共有( )种不同的穿法。
A.4 B.5 C.6
21.(本题2分)三位同学竞选体育委员和卫生委员各1名,一共有( )种不同的竞选结果。
A.4 B.6 C.8
四、连线题(共6分)
22.(本题6分)我来做“小厨(chú )师”﹣﹣“午餐(cān)搭配”.
请你从下面的5种食品中选出2种来作为我们的“午餐”,其中一种是主食,另一种是副食.(①②为主食,③④⑤为副食.)可以有几种不同的搭配方法?请用线连接起来.
五、作图题(共4分)
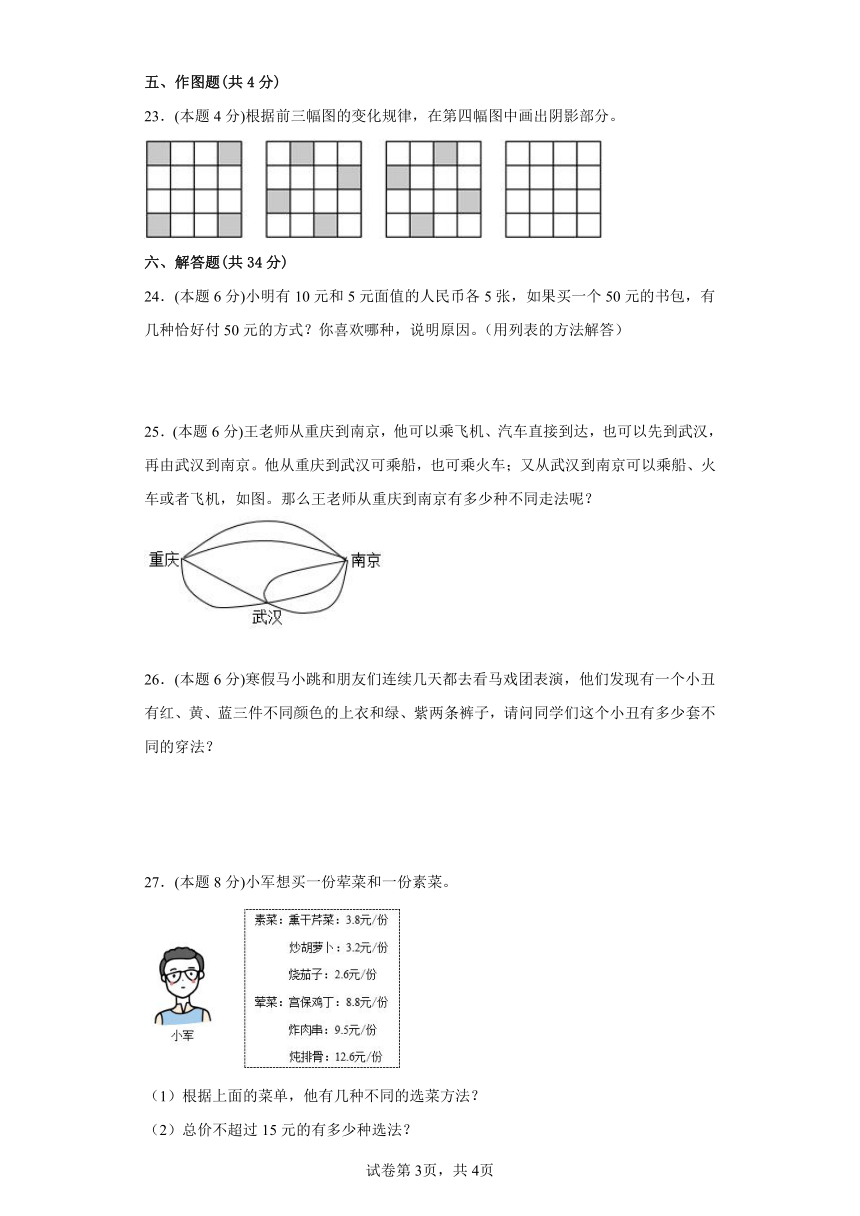
23.(本题4分)根据前三幅图的变化规律,在第四幅图中画出阴影部分。
六、解答题(共34分)
24.(本题6分)小明有10元和5元面值的人民币各5张,如果买一个50元的书包,有几种恰好付50元的方式?你喜欢哪种,说明原因。(用列表的方法解答)
25.(本题6分)王老师从重庆到南京,他可以乘飞机、汽车直接到达,也可以先到武汉,再由武汉到南京。他从重庆到武汉可乘船,也可乘火车;又从武汉到南京可以乘船、火车或者飞机,如图。那么王老师从重庆到南京有多少种不同走法呢?
(本题6分)寒假马小跳和朋友们连续几天都去看马戏团表演,他们发现有一个小丑有红、黄、蓝三件不同颜色的上衣和绿、紫两条裤子,请问同学们这个小丑有多少套不同的穿法?
27.(本题8分)小军想买一份荤菜和一份素菜。
(1)根据上面的菜单,他有几种不同的选菜方法?
(2)总价不超过15元的有多少种选法?
(3)最便宜的搭配要花多少元?
28.(本题8分)书店新进了4种书。丽丽有几种不同的选法?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 18 752
【解析】
【分析】
(1)从2、7、0、5四个数字卡片中任取三张组成不同的三位数,百位上可选择2、5、7,共有3种选法;百位选完后,还剩下3个数,则十位上有3种选法;百位和十位选完后剩下2个数字,个位上有2种选法;那么可以组成(3×3×2)个不同的三位数;
(2)从2、7、0、5四个数字卡片中任取三张组成最大的三位数,选择最大的数字在最高位,百位选7;十位选择剩下三个数字中最大的5,个位选择剩下两个数字中最大的2,组成最大的三位数是752。
【详解】
3×3×2=18(个)
百位选7,十位选5,个位选2,组成最大的三位数是752。
【点睛】
本题主要考查排列组合知识,排列组合的乘法原理是解决排列组合问题的常用方法。
2. 6 396
【解析】
【分析】
先将3、7、5组成的三位数写出来,找出最大和最小的数,再求出差即可。
【详解】
3、7、5组成的三位数有:375,357,573,537,753,735共6个不同的三位数;
最大753,最小是357
753-357=396
【点睛】
本题考查简单的排列、组合的方法以及应用,关键是按照一定的顺序写书,注意不要漏写和重复写。
3. 652 125 527
【解析】
【分析】
要想组成的数最大,要把数按照从大到小的顺序从高位到低位排下来;要想组成的数最小,要把数按照从小到大的顺序从高位到低位排下来,但是最高位不能是零;再求出它们的差即可。
【详解】
因为6>5>2>1,
所以,用6,5,2,1四张卡片能组成的最大三位数是652,能组成的最小三位数是125,它们相差652-125=527。
【点睛】
本题主要考查数的组成方法,组大数时:按照从大到小的顺序把数从高位排下来,组小数时:按照从小到大的顺序把数从高位排下来,注意0不能放在最高位。
4.6
【解析】
【分析】
最左边的猪八戒站着不动,后面可以是唐僧、沙僧和孙悟空,或者唐僧、孙悟空和沙僧。也可以是沙僧、唐僧和孙悟空,或者沙僧、孙悟空和唐僧。还可以是孙悟空、唐僧和沙僧,孙悟空、沙僧和唐僧。据此可知一共有6种站法。
【详解】
唐僧师徒四人排成一排照相,如果最左边的猪八戒站着不动,其他三人可以任意调换位置,一共有6种站法。
【点睛】
本题考查搭配问题,可以采用列举法,应按照顺序数,才能不重不漏。
5.15
【解析】
【分析】
因为每一名同学都要和其他(6-1)名同学比赛;每人比赛5场,一共比赛5×6=30场;但两人之间重复一次,因此需要比赛的场次是30÷2,据此解答。
【详解】
6×(6-1)÷2
=6×5÷2
=15(场)
【点睛】
在循环赛制中,参赛人数和比赛场数的关系:比赛场次=参赛人数×(参赛人数-1)÷2。
6.10
【解析】
【分析】
由于每个城市都要和另外的4个城市修一条高速公路,一共要修高速公路:4×5=20(条);又因为两个城市只修一条高速公路,去掉重复计算的情况,实际只修了:20÷2=10(条),据此解答。
【详解】
(5-1)×5÷2
=20÷2
=10(条)
【点睛】
本题考查了排列组合问题的实际应用,要注意去掉重复计算的情况,如果城市数比较少可以用枚举法解答,如果城市数比较多可以用公式:条数=n(n-1)÷2解答。
7. 6 7.65
【解析】
【分析】
由三个数字组成两位小数,则这个小数的整数部分只有个位上的数,小数部分有十分位和百分位上的数。当个位上的5时,可以组成5.67、5.76。当个位上是6时,可以组成6.57、6.75。当个位上是7时,可以组成7.56、7.65。再将这几个小数比较大小解答。
【详解】
7.65>7.56>6.75>6.57>5.76>5.67
用5、7和6这三个数字可以写出6个没有重复的两位小数,其中最大的是7.65
【点睛】
搭配问题中,可以采用枚举法解答。要注意按一定的顺序,才能做到不重不漏。小数比较大小时,从高位起,依次比较相同数位上的数。
8.6
【解析】
【分析】
根据搭配的方法可知,何一跑第一棒固定,因此第二棒有3种可能,第三棒就有2种可能,第四棒就只有1种可能,然后将每一棒的可能数加起来即可。
【详解】
3+2+1=6(种)
【点睛】
熟练掌握搭配问题的计算是解答此题的关键。
9.7
【解析】
【分析】
先分类,右盘放1个砝码,2个砝码或3个砝码共三类情况,然后再一一列举出来各种情况,如果有相同的情况,要注意排除。
【详解】
放1个砝码:1克,2克,5克;
放2个砝码:1+2=3(克),1+5=6(克),2+5=7(克)
放3个砝码:1+2+5=8(克)
共有7种不同的质量。
【点睛】
本题考查列举法的应用,列举时做到有序列举才能不重不漏。
10.6
【解析】
【分析】
根据题意,一本故事书分别与每本科技书搭配一次,就有2种不同的搭配方法,那么3本故事书就有(2×3)本搭配方法,据此解题即可。
【详解】
2×3=6(种)
所以,班级图书角有3本故事书,2本科技书。李刚两种书各借一本,有6种不同的选择方法。
【点睛】
熟练掌握搭配问题的解题方法,是解答此题的关键。
11.3
【解析】
【详解】
略
12.×
【解析】
【分析】
此题是组合问题,其中任意一道和其他四道中选择三道进行搭配,有3种,一共有4个3,列式即可解答;也可以用列举法或连线法解答。
【详解】
因为4×3=12(种)所以,此题说法错误。
故答案为:×
【点睛】
此题是组合问题,注意:不要重复或遗漏,组合问题和顺序无关。
13.√
【解析】
【分析】
假设有A、B、C、D、E五个人,将它们两两搭配,将所有搭配方法画出来,然后再判断。
【详解】
因此5人中每2人通一次电话,一共要通10次电话。
故答案为:√
【点睛】
熟练掌握搭配问题的计算是解答此题的关键。
14.×
【解析】
【分析】
先将甲、乙、丙、丁两两搭配,有甲乙、甲丙、甲丁、乙丙、乙丁、丙丁,共六种搭配方式。每一种搭配,如甲乙,可能甲为班长,乙为副班长,也可能甲为副班长,乙为班长,每一种搭配里面又有两种选择,所以一共有6×2=12种选法,据此即可解答。
【详解】
根据分析可知,要从甲、乙、丙、丁中选出1名班长和1名副班长,一共有:3×4÷2×2=12÷2×2=6×2=12(种)。
故题干说法错误。
【点睛】
本题考查的是搭配问题,除了考虑甲、乙、丙、丁的二者搭配,还需要考虑班长和副班长二者可调换位置。
15.错误
【解析】
【详解】
试题分析:因为没有说是站成横队还是纵队,所以从前到后的顺序,从后到前;从左到右或从右到左排列方法都不同,据此解答即可.
解:由分析得出:5个身高各不相同的同学按从高到矮的顺序排列,只能有1种排法说法错误.
故答案为错误.
点评:解决本题的关键是明确方向的不同也会造成排列方法的不同.
16.B
【解析】
如果4个同学互相赠一张贺卡,每个人都要得到另外的3个人的3张,由于每两人要互送,-共需要:3×4=12张贺卡,据此解答。
【详解】
4×(4-1)
=4×3
=12(张)
一共需要12张贺卡。
故选择:B。
【点睛】
此题考查了搭配问题,要注意区分互赠与握手问题。
17.B
【解析】
【分析】
十位上是3时,可以组成30、35、37三个没有重复数字的两位数,同理十位上是5、7时都可以分别组成三个没有重复数字的两位数,共可以组成3×3=9个没有重复数字的两位数。
【详解】
根据分析可知,用3、0、5、7能组成3×3=9(个)没有重复数字的两位数。
故答案为:B。
【点睛】
解答本题时要注意,0不能放在十位上。
18.C
【解析】
【分析】
首先用书包的价格除以5,判断出买这个书包需要多少张5元的人民币,然后根据每减少2张5元的人民币就需要增加5张2元的人民币,据此判断即可。
【详解】
30÷5=6(张)
(1)6张5元的的人民币;
(2)4张5元的人民币和5张2元的人民币;
共2种恰好支付的方式,故答案选:C。
【点睛】
本题考查搭配问题的应用,可以一一排列组合选择。
19.C
【解析】
略
20.C
【解析】
【分析】
根据题意可知,每件上衣都可以与3条裤子搭配,所以有3种穿法;每条裤子都可以与2件上衣搭配,所以有2种穿法。则2件上衣搭配3条裤子一共就有2×3种不同的穿法;据此解答即可。
【详解】
2×3=6(种)
则一共有6种不同的穿法。
故答案为:C。
【点睛】
本题考查了排列组合中的乘法原理,需要明确2件上衣和3条裤子各有几种选择,然后相乘即可得解。
21.B
【解析】
【分析】
从三人中选一位当体育委员有3种选法,从剩余的两人中选一人当卫生委员有2种选法,根据乘法原理可得:一共有3×2=6种不同的选法。
【详解】
3×2=6(种)
故答案为:B
【点睛】
本题考查了乘法原理即做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法……,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×……×Mn种不同的方法。
22.
【解析】
【详解】
试题分析:从2种是主食中选一种有2种选法;从3种是副食中选一种有3种选法;根据乘法原理,可得共有:2×3=6(种);据此解答.
解:2×3=6(种);
答:可以有6种不同的搭配方法.
故用线连接如右图:
点评:本题考查了乘法原理即做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法,…,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×…×Mn种不同的方法.
23.见详解
【解析】
【分析】
观察图形可知,图形中的阴影部分的四个小正方形分别绕大正方形的四周顺时针依次移动1格,即可得出后面的图形,据此即可画图
【详解】
【点睛】
主要考查了学生通过特例分析从而归纳总结出一般结论的能力。对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解。
24.见详解
【解析】
【分析】
先全部付10元的人民币得5张,然后10元人民币张数逐渐减少,5元人民币张数增加,注意10元减少1张,5元得增加2张,但5元人民币不得超过5张,据此列表即可解答
【详解】
方案 10元 5元 总钱数
① 5张 0张 50元
② 4张 2张 50元
③ 3张 4张 50元
一共有3种方式,我喜欢付5张10元,这样简单。
【点睛】
不管哪种方式,付出10元和5元面值的人民币钱数和等于50元,这是解答本题的关键。
25.8种
【解析】
【分析】
从重庆到南京的走法有两类:第一类从重庆经过武汉去南京,第二类不经过武汉,直接去南京,两种的方法数相加,得到总数。
【详解】
第一类:
(种)
第二类:有2种走法;
根据加法原理,从重庆到南京一共有种不同走法。
答:从重庆到南京一共有8种不同走法。
【点睛】
本题考查的是加乘原理的计数问题,加法分类,类类相加,乘法分步,步步相乘。
26.6套
【解析】
【分析】
根据题意,用画图连线的形式表示出裤子和上衣,连线表示一种穿法,数出连线数即可。
【详解】
搭配方式如图:
由图可知总共有6套不同的穿法。
答:小丑有6套不同的穿法。
【点睛】
本题为典型的搭配问题,用图示方法个人能够容易理解搭配问题的解法。
27.(1)9种
(2)6种
(3)11.4元
【解析】
【分析】
(1)小军要选一份荤菜和一份,菜单中荤菜共3种,青菜也是3种,共有3×3=9(种)不同的选菜方法;
(2)将每一种搭配按照价钱算出来与15元进行比较即可知道总价不超过15元的有多少种选法;
(3)根据第二问直接得到最便宜的搭配方法。
【详解】
(1)3×3=9(种)
答:他有9种不同的选菜方法。
(2)熏干芹菜+宫保鸡丁=3.8+8.8=12.6(元)<15元;
熏干芹菜+炸肉串=3.8+9.5=13.3(元)<15元;
熏干芹菜+炖排骨=3.8+12.6=16.4(元);
炒胡萝卜+宫保鸡丁=3.2+8.8=12(元)<15元;
炒胡萝卜+炸肉串=3.2+9.5=12.7(元)<15元;
炒胡萝卜+炖排骨=3.2+12.6=15.8(元);
烧茄子+宫保鸡丁=2.6+8.8=11.4(元)<15元;
烧茄子+炸肉串=2.6+9.5=12.1(元)<15元;
烧茄子+炖排骨=2.6+12.6=15.2(元);
答:总价不超过15元的有6种选法。
(3)最便宜的为烧茄子+宫保鸡丁=2.6+8.8=11.4(元)
答:最便宜的搭配要花11.4元。
【点睛】
本题考查的是简单的搭配问题,关键是注意搞清楚搭配,做到不重不漏。
28.6种
【解析】
【详解】
4本书分别用A、B、C、D表示,则有以下6种选法:AB、AC、AD、BC、BD、CD。
答:丽丽有6种不同的选法。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 六 总分
得分
一、填空题(共36分)
1.(本题4分)从2、7、0、5中任取三个数字,可以组成( )个不同的三位数,在这些三位数中,最大的是( )。
2.(本题4分)数字3、7、5共可以组成( )个不同的三位数,其中最大数比最小数多( )。
3.(本题3分)用6,5,2,1四张卡片能组成的最大三位数是( ),能组成的最小三位数是( ),它们相差( )。
4.(本题3分)唐僧师徒四人排成一排照相,如果最左边的猪八戒站着不动,其他三人可以任意调换位置,一共有( )种站法。
5.(本题3分)6名同学进行象棋比赛,如果每两人赛一场,一共要赛( )场。
6.(本题3分)有5个城市,每两个城市之间修一条高速公路,可以修( ) 条高速公路。
7.(本题4分)用5、7和6这三个数字可以写出( )个没有重复的两位小数,其中最大的是( )。
8.(本题3分)运动会上,301班何一、沈倩、王晓、刘丽将参加女子组4×100米接力赛,何一跑得最快,体育老师已经将她排在第一棒。这四名同学跑接力赛一共有( )种排法。
9.(本题3分)现有1克、2克、5克的砝码各一个(砝码只能放在右盘),在天平上最多能称出( )种不同的质量。
10.(本题3分)班级图书角有3本故事书,2本科技书。李刚两种书各借一本,有( )种不同的选择方法。
11.(本题3分)从3、4、5这三个数中,任意选其中两个数组成乘法算式,有________种不同的积。
二、判断题(共8分)
12.(本题2分)有5道不同的计算题,小明任意选4道做,共有20种不同选法。( )
13.(本题2分)5人中每2人通一次电话,一共要通10次电话。( )
14.(本题2分)李老师要从甲、乙、丙、丁中选出1名班长和1名副班长,共有14种不同的选法。( )
15.(本题2分)5个身高各不相同的同学按从高到矮的顺序排列,只能有1种排法.。( )
三、选择题(共12分)
16.(本题2分)明明、红红、丽丽、君君在元旦前互赠1张贺卡,一共需要( )张贺卡。
A.4 B.12 C.16
17.(本题2分)用3、0、5、7能组成( )个没有重复数字的两位数。
A.6 B.9 C.12
18.(本题2分)小明有5元和2元面值的人民币各6张,如果要买一个30元的书包,有几种恰好付给30元的方式?( )
A.4种 B.3种 C.2种
19.(本题2分)下图有几个长方形?( )
A.5个 B.8个 C.9个
20.(本题2分)兰兰有两件上衣、三条裤子,每次上装和下装各穿一件,一共有( )种不同的穿法。
A.4 B.5 C.6
21.(本题2分)三位同学竞选体育委员和卫生委员各1名,一共有( )种不同的竞选结果。
A.4 B.6 C.8
四、连线题(共6分)
22.(本题6分)我来做“小厨(chú )师”﹣﹣“午餐(cān)搭配”.
请你从下面的5种食品中选出2种来作为我们的“午餐”,其中一种是主食,另一种是副食.(①②为主食,③④⑤为副食.)可以有几种不同的搭配方法?请用线连接起来.
五、作图题(共4分)
23.(本题4分)根据前三幅图的变化规律,在第四幅图中画出阴影部分。
六、解答题(共34分)
24.(本题6分)小明有10元和5元面值的人民币各5张,如果买一个50元的书包,有几种恰好付50元的方式?你喜欢哪种,说明原因。(用列表的方法解答)
25.(本题6分)王老师从重庆到南京,他可以乘飞机、汽车直接到达,也可以先到武汉,再由武汉到南京。他从重庆到武汉可乘船,也可乘火车;又从武汉到南京可以乘船、火车或者飞机,如图。那么王老师从重庆到南京有多少种不同走法呢?
(本题6分)寒假马小跳和朋友们连续几天都去看马戏团表演,他们发现有一个小丑有红、黄、蓝三件不同颜色的上衣和绿、紫两条裤子,请问同学们这个小丑有多少套不同的穿法?
27.(本题8分)小军想买一份荤菜和一份素菜。
(1)根据上面的菜单,他有几种不同的选菜方法?
(2)总价不超过15元的有多少种选法?
(3)最便宜的搭配要花多少元?
28.(本题8分)书店新进了4种书。丽丽有几种不同的选法?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 18 752
【解析】
【分析】
(1)从2、7、0、5四个数字卡片中任取三张组成不同的三位数,百位上可选择2、5、7,共有3种选法;百位选完后,还剩下3个数,则十位上有3种选法;百位和十位选完后剩下2个数字,个位上有2种选法;那么可以组成(3×3×2)个不同的三位数;
(2)从2、7、0、5四个数字卡片中任取三张组成最大的三位数,选择最大的数字在最高位,百位选7;十位选择剩下三个数字中最大的5,个位选择剩下两个数字中最大的2,组成最大的三位数是752。
【详解】
3×3×2=18(个)
百位选7,十位选5,个位选2,组成最大的三位数是752。
【点睛】
本题主要考查排列组合知识,排列组合的乘法原理是解决排列组合问题的常用方法。
2. 6 396
【解析】
【分析】
先将3、7、5组成的三位数写出来,找出最大和最小的数,再求出差即可。
【详解】
3、7、5组成的三位数有:375,357,573,537,753,735共6个不同的三位数;
最大753,最小是357
753-357=396
【点睛】
本题考查简单的排列、组合的方法以及应用,关键是按照一定的顺序写书,注意不要漏写和重复写。
3. 652 125 527
【解析】
【分析】
要想组成的数最大,要把数按照从大到小的顺序从高位到低位排下来;要想组成的数最小,要把数按照从小到大的顺序从高位到低位排下来,但是最高位不能是零;再求出它们的差即可。
【详解】
因为6>5>2>1,
所以,用6,5,2,1四张卡片能组成的最大三位数是652,能组成的最小三位数是125,它们相差652-125=527。
【点睛】
本题主要考查数的组成方法,组大数时:按照从大到小的顺序把数从高位排下来,组小数时:按照从小到大的顺序把数从高位排下来,注意0不能放在最高位。
4.6
【解析】
【分析】
最左边的猪八戒站着不动,后面可以是唐僧、沙僧和孙悟空,或者唐僧、孙悟空和沙僧。也可以是沙僧、唐僧和孙悟空,或者沙僧、孙悟空和唐僧。还可以是孙悟空、唐僧和沙僧,孙悟空、沙僧和唐僧。据此可知一共有6种站法。
【详解】
唐僧师徒四人排成一排照相,如果最左边的猪八戒站着不动,其他三人可以任意调换位置,一共有6种站法。
【点睛】
本题考查搭配问题,可以采用列举法,应按照顺序数,才能不重不漏。
5.15
【解析】
【分析】
因为每一名同学都要和其他(6-1)名同学比赛;每人比赛5场,一共比赛5×6=30场;但两人之间重复一次,因此需要比赛的场次是30÷2,据此解答。
【详解】
6×(6-1)÷2
=6×5÷2
=15(场)
【点睛】
在循环赛制中,参赛人数和比赛场数的关系:比赛场次=参赛人数×(参赛人数-1)÷2。
6.10
【解析】
【分析】
由于每个城市都要和另外的4个城市修一条高速公路,一共要修高速公路:4×5=20(条);又因为两个城市只修一条高速公路,去掉重复计算的情况,实际只修了:20÷2=10(条),据此解答。
【详解】
(5-1)×5÷2
=20÷2
=10(条)
【点睛】
本题考查了排列组合问题的实际应用,要注意去掉重复计算的情况,如果城市数比较少可以用枚举法解答,如果城市数比较多可以用公式:条数=n(n-1)÷2解答。
7. 6 7.65
【解析】
【分析】
由三个数字组成两位小数,则这个小数的整数部分只有个位上的数,小数部分有十分位和百分位上的数。当个位上的5时,可以组成5.67、5.76。当个位上是6时,可以组成6.57、6.75。当个位上是7时,可以组成7.56、7.65。再将这几个小数比较大小解答。
【详解】
7.65>7.56>6.75>6.57>5.76>5.67
用5、7和6这三个数字可以写出6个没有重复的两位小数,其中最大的是7.65
【点睛】
搭配问题中,可以采用枚举法解答。要注意按一定的顺序,才能做到不重不漏。小数比较大小时,从高位起,依次比较相同数位上的数。
8.6
【解析】
【分析】
根据搭配的方法可知,何一跑第一棒固定,因此第二棒有3种可能,第三棒就有2种可能,第四棒就只有1种可能,然后将每一棒的可能数加起来即可。
【详解】
3+2+1=6(种)
【点睛】
熟练掌握搭配问题的计算是解答此题的关键。
9.7
【解析】
【分析】
先分类,右盘放1个砝码,2个砝码或3个砝码共三类情况,然后再一一列举出来各种情况,如果有相同的情况,要注意排除。
【详解】
放1个砝码:1克,2克,5克;
放2个砝码:1+2=3(克),1+5=6(克),2+5=7(克)
放3个砝码:1+2+5=8(克)
共有7种不同的质量。
【点睛】
本题考查列举法的应用,列举时做到有序列举才能不重不漏。
10.6
【解析】
【分析】
根据题意,一本故事书分别与每本科技书搭配一次,就有2种不同的搭配方法,那么3本故事书就有(2×3)本搭配方法,据此解题即可。
【详解】
2×3=6(种)
所以,班级图书角有3本故事书,2本科技书。李刚两种书各借一本,有6种不同的选择方法。
【点睛】
熟练掌握搭配问题的解题方法,是解答此题的关键。
11.3
【解析】
【详解】
略
12.×
【解析】
【分析】
此题是组合问题,其中任意一道和其他四道中选择三道进行搭配,有3种,一共有4个3,列式即可解答;也可以用列举法或连线法解答。
【详解】
因为4×3=12(种)所以,此题说法错误。
故答案为:×
【点睛】
此题是组合问题,注意:不要重复或遗漏,组合问题和顺序无关。
13.√
【解析】
【分析】
假设有A、B、C、D、E五个人,将它们两两搭配,将所有搭配方法画出来,然后再判断。
【详解】
因此5人中每2人通一次电话,一共要通10次电话。
故答案为:√
【点睛】
熟练掌握搭配问题的计算是解答此题的关键。
14.×
【解析】
【分析】
先将甲、乙、丙、丁两两搭配,有甲乙、甲丙、甲丁、乙丙、乙丁、丙丁,共六种搭配方式。每一种搭配,如甲乙,可能甲为班长,乙为副班长,也可能甲为副班长,乙为班长,每一种搭配里面又有两种选择,所以一共有6×2=12种选法,据此即可解答。
【详解】
根据分析可知,要从甲、乙、丙、丁中选出1名班长和1名副班长,一共有:3×4÷2×2=12÷2×2=6×2=12(种)。
故题干说法错误。
【点睛】
本题考查的是搭配问题,除了考虑甲、乙、丙、丁的二者搭配,还需要考虑班长和副班长二者可调换位置。
15.错误
【解析】
【详解】
试题分析:因为没有说是站成横队还是纵队,所以从前到后的顺序,从后到前;从左到右或从右到左排列方法都不同,据此解答即可.
解:由分析得出:5个身高各不相同的同学按从高到矮的顺序排列,只能有1种排法说法错误.
故答案为错误.
点评:解决本题的关键是明确方向的不同也会造成排列方法的不同.
16.B
【解析】
如果4个同学互相赠一张贺卡,每个人都要得到另外的3个人的3张,由于每两人要互送,-共需要:3×4=12张贺卡,据此解答。
【详解】
4×(4-1)
=4×3
=12(张)
一共需要12张贺卡。
故选择:B。
【点睛】
此题考查了搭配问题,要注意区分互赠与握手问题。
17.B
【解析】
【分析】
十位上是3时,可以组成30、35、37三个没有重复数字的两位数,同理十位上是5、7时都可以分别组成三个没有重复数字的两位数,共可以组成3×3=9个没有重复数字的两位数。
【详解】
根据分析可知,用3、0、5、7能组成3×3=9(个)没有重复数字的两位数。
故答案为:B。
【点睛】
解答本题时要注意,0不能放在十位上。
18.C
【解析】
【分析】
首先用书包的价格除以5,判断出买这个书包需要多少张5元的人民币,然后根据每减少2张5元的人民币就需要增加5张2元的人民币,据此判断即可。
【详解】
30÷5=6(张)
(1)6张5元的的人民币;
(2)4张5元的人民币和5张2元的人民币;
共2种恰好支付的方式,故答案选:C。
【点睛】
本题考查搭配问题的应用,可以一一排列组合选择。
19.C
【解析】
略
20.C
【解析】
【分析】
根据题意可知,每件上衣都可以与3条裤子搭配,所以有3种穿法;每条裤子都可以与2件上衣搭配,所以有2种穿法。则2件上衣搭配3条裤子一共就有2×3种不同的穿法;据此解答即可。
【详解】
2×3=6(种)
则一共有6种不同的穿法。
故答案为:C。
【点睛】
本题考查了排列组合中的乘法原理,需要明确2件上衣和3条裤子各有几种选择,然后相乘即可得解。
21.B
【解析】
【分析】
从三人中选一位当体育委员有3种选法,从剩余的两人中选一人当卫生委员有2种选法,根据乘法原理可得:一共有3×2=6种不同的选法。
【详解】
3×2=6(种)
故答案为:B
【点睛】
本题考查了乘法原理即做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法……,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×……×Mn种不同的方法。
22.
【解析】
【详解】
试题分析:从2种是主食中选一种有2种选法;从3种是副食中选一种有3种选法;根据乘法原理,可得共有:2×3=6(种);据此解答.
解:2×3=6(种);
答:可以有6种不同的搭配方法.
故用线连接如右图:
点评:本题考查了乘法原理即做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法,…,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×…×Mn种不同的方法.
23.见详解
【解析】
【分析】
观察图形可知,图形中的阴影部分的四个小正方形分别绕大正方形的四周顺时针依次移动1格,即可得出后面的图形,据此即可画图
【详解】
【点睛】
主要考查了学生通过特例分析从而归纳总结出一般结论的能力。对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解。
24.见详解
【解析】
【分析】
先全部付10元的人民币得5张,然后10元人民币张数逐渐减少,5元人民币张数增加,注意10元减少1张,5元得增加2张,但5元人民币不得超过5张,据此列表即可解答
【详解】
方案 10元 5元 总钱数
① 5张 0张 50元
② 4张 2张 50元
③ 3张 4张 50元
一共有3种方式,我喜欢付5张10元,这样简单。
【点睛】
不管哪种方式,付出10元和5元面值的人民币钱数和等于50元,这是解答本题的关键。
25.8种
【解析】
【分析】
从重庆到南京的走法有两类:第一类从重庆经过武汉去南京,第二类不经过武汉,直接去南京,两种的方法数相加,得到总数。
【详解】
第一类:
(种)
第二类:有2种走法;
根据加法原理,从重庆到南京一共有种不同走法。
答:从重庆到南京一共有8种不同走法。
【点睛】
本题考查的是加乘原理的计数问题,加法分类,类类相加,乘法分步,步步相乘。
26.6套
【解析】
【分析】
根据题意,用画图连线的形式表示出裤子和上衣,连线表示一种穿法,数出连线数即可。
【详解】
搭配方式如图:
由图可知总共有6套不同的穿法。
答:小丑有6套不同的穿法。
【点睛】
本题为典型的搭配问题,用图示方法个人能够容易理解搭配问题的解法。
27.(1)9种
(2)6种
(3)11.4元
【解析】
【分析】
(1)小军要选一份荤菜和一份,菜单中荤菜共3种,青菜也是3种,共有3×3=9(种)不同的选菜方法;
(2)将每一种搭配按照价钱算出来与15元进行比较即可知道总价不超过15元的有多少种选法;
(3)根据第二问直接得到最便宜的搭配方法。
【详解】
(1)3×3=9(种)
答:他有9种不同的选菜方法。
(2)熏干芹菜+宫保鸡丁=3.8+8.8=12.6(元)<15元;
熏干芹菜+炸肉串=3.8+9.5=13.3(元)<15元;
熏干芹菜+炖排骨=3.8+12.6=16.4(元);
炒胡萝卜+宫保鸡丁=3.2+8.8=12(元)<15元;
炒胡萝卜+炸肉串=3.2+9.5=12.7(元)<15元;
炒胡萝卜+炖排骨=3.2+12.6=15.8(元);
烧茄子+宫保鸡丁=2.6+8.8=11.4(元)<15元;
烧茄子+炸肉串=2.6+9.5=12.1(元)<15元;
烧茄子+炖排骨=2.6+12.6=15.2(元);
答:总价不超过15元的有6种选法。
(3)最便宜的为烧茄子+宫保鸡丁=2.6+8.8=11.4(元)
答:最便宜的搭配要花11.4元。
【点睛】
本题考查的是简单的搭配问题,关键是注意搞清楚搭配,做到不重不漏。
28.6种
【解析】
【详解】
4本书分别用A、B、C、D表示,则有以下6种选法:AB、AC、AD、BC、BD、CD。
答:丽丽有6种不同的选法。
答案第1页,共2页
答案第1页,共2页
