3.2用关系式表示的变量间关系 课件(共27张PPT)
文档属性
| 名称 | 3.2用关系式表示的变量间关系 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 20:31:34 | ||
图片预览



文档简介
(共27张PPT)
北师大版七年级下册数学
第三章 变量之间的关系
3.2用关系式表示的变量间关系
游戏:数青蛙
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿;
……
1.青蛙的眼睛数和只数有关系吗?能用数学式表达吗?
2.青蛙的腿数和只数有关系吗?能用数学式表达吗?
这个游戏你能继续玩下去吗?
情景引入
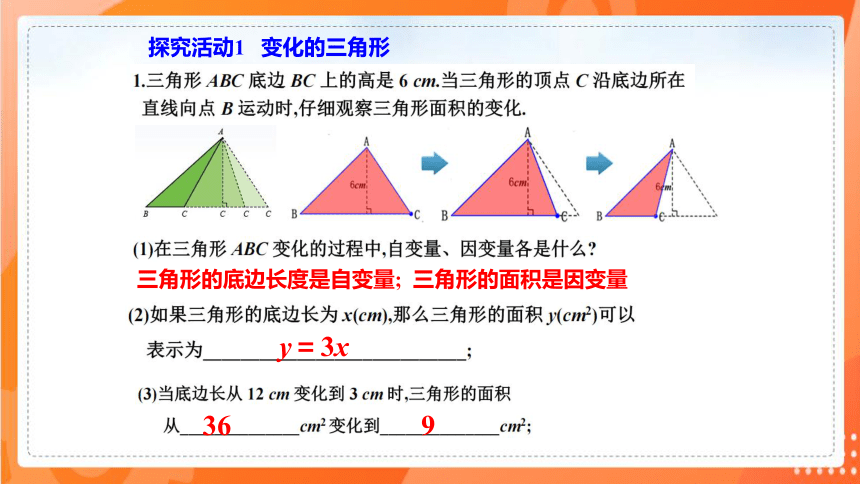
探究活动1 变化的三角形
y=3x
36
9
三角形的底边长度是自变量; 三角形的面积是因变量
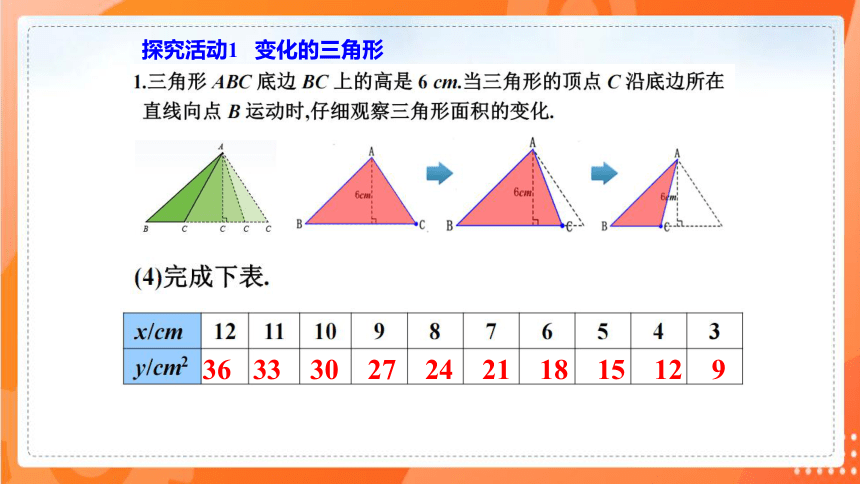
探究活动1 变化的三角形
36 33 30 27 24 21 18 15 12 9
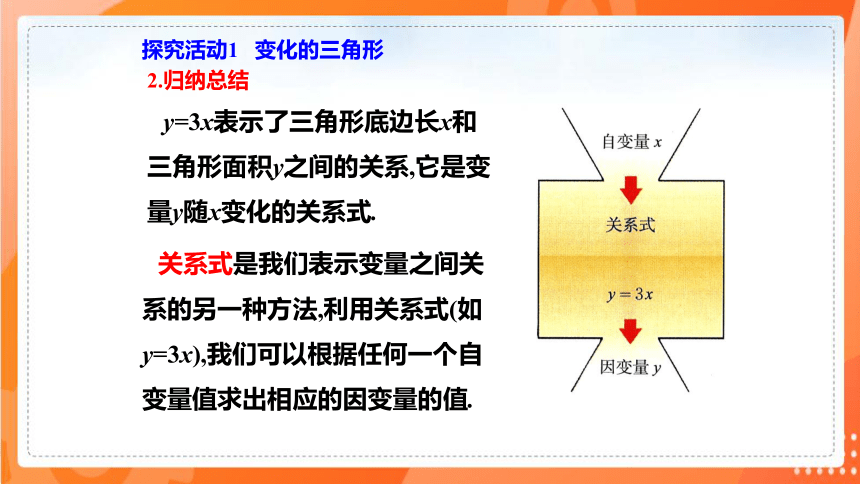
关系式是我们表示变量之间关系的另一种方法,利用关系式(如y=3x),我们可以根据任何一个自变量值求出相应的因变量的值.
y=3x表示了三角形底边长x和三角形面积y之间的关系,它是变量y随x变化的关系式.
探究活动1 变化的三角形
2.归纳总结
探究活动2 表格和关系式对比
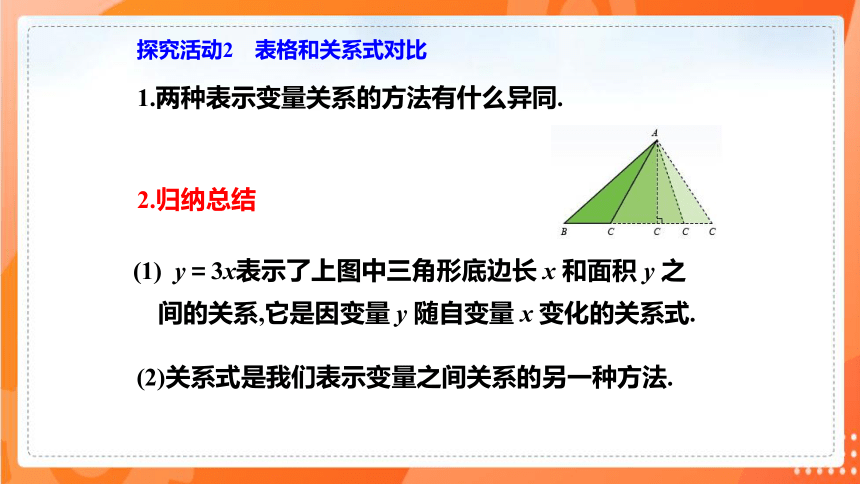
1.两种表示变量关系的方法有什么异同.
2.归纳总结
(2)关系式是我们表示变量之间关系的另一种方法.
(1) y=3x表示了上图中三角形底边长 x 和面积 y 之
间的关系,它是因变量 y 随自变量 x 变化的关系式.
探究活动2 表格和关系式对比
2.归纳总结
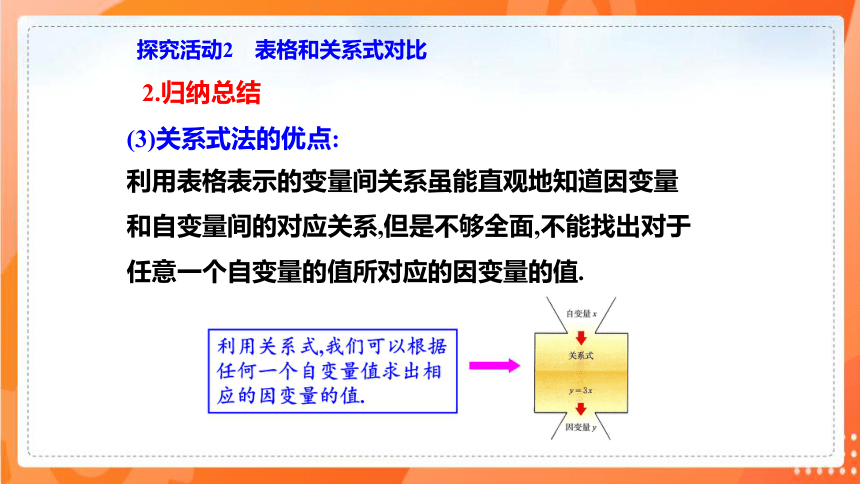
(3)关系式法的优点:
利用表格表示的变量间关系虽能直观地知道因变量
和自变量间的对应关系,但是不够全面,不能找出对于
任意一个自变量的值所对应的因变量的值.
自变量为圆锥的底面半径,
因变量为圆锥的体积
1.用来表示自变量和因变量之间关系的等式叫做关系式
要点精析:
关系式的基本特征是:
①等式的左边是因变量,等式的右边是关于自变
量的代数式;
②等式中只含有自变量和因变量这两个变量,其
他的量都是常量;
③自变量可在允许的范围内任意取值.
小结
2.求两个变量之间的关系式常用的方法:
(1)利用公式:如图形的周长公式、面积公式、体积公
式等;
(2)利用生活中特定的数量 关系,如行程问题中“路
程=时间×速度”,销售问题中“销售额=单价×
数量”等;
(3)根据表格与图象中的信息列关系式(这种方法以后
会学习)等.
例1
长方形的周长为24 cm,其中一边长为x cm(x>0),面积为y cm2,则该长方形中y与x的关系可以写为
( )
A.y=x2 B.y=(12-x)2
C.y=(12-x)·x D.y=2(12-x)
因为长方形的周长为24 cm,其中一边长为x cm,
所以另一边长为(12-x) cm,因为面积为y cm2,
所以该长方形中y与x的关系可以写为y=(12-x)·x.
导引:
C
典型例题
例2
百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其销售量x(米)与售价y(元)如下表:
下列用销售量x(米)表示售价y(元)的关系式中,正确的是
( )
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
通过观察表格内x与y的关系,可知y的值相对于x=1时是
成倍增长的,由此可得y=(8+0.3)x.
导引:
销售量x/米 1 2 3 4 …
售价y/元 8+0.3 16+0.6 24+0.9 32+1.2 …
B
议一议
你知道什么是“低碳生活”吗? “低碳生活”
是指人们生活中尽量减少所耗能量,从而降低碳(特
别是二氧化碳)的排放量的一种生活方式.
用关系式求值
y = 0.785x
y 表示二氧化碳的排放量(kg),
x 表示的是耗电量(kW·h)
0.785 kg
0.785 kg
78.5 kg
提示:根据上面的排碳计算公式,
用电排放的二氧化碳数量为0.785×110=86.35(kg);
用天然气排放的二氧化碳数量为20×0.19=3.8(kg);
用自来水排放的二氧化碳数量为5×0.91=4.55(kg);
开私家车耗油排放的二氧化碳数量为75×2.7=202.5(kg).
以上各项相加得297.2 kg.
即小明家这几项的二氧化碳排放量为297.2 kg
例3
某工厂现在年产值是15万元,计划今后每年增加2
万元.
(1)年产值y(万元)与年数x之间的关系式为 __________;
(2)5年后的年产值是______万元.
(1)根据题意可知,现在年产值是15万元,计划今后
每年增加2万元,x年后增加2x万元,所以年产值
y(万元)与年数x之间的关系式为y=2x+15;
(2)将x=5代入关系式得:y=2x+15=2×5+15=25.
导引:
y=2x+15
25
典型例题
1.变量x与y之间的关系式是y=x2-3,当自变量x=2
时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
C
【解析】将x=2代入y=x2-3,得y=22-3=1.
课堂练习
2.一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为( )
A.y=2x B.y=10-2x
C.y=5x D.y=10-5x
【解析】由题意,有y=2(5-x),即y=10-2x.
B
3.如图是一个简单的数值运算程序,当输入x的值
为1时,则输出的数值为____.
【解析】根据程序,计算过程可以表示为:-x+3,
所以当x=1时,原式=-1+3=2.
4.在关系式S=40t中,当t=1.5时,S=____.
【解析】把t=1.5代入S=40t中,得S=40×1.5=60.
60
2
5.已知水池中有800立方米的水,每小时抽50立方米.
(1)写出剩余水的体积Q(立方米)与时间t(小时)之间的关系式;
(2)6小时后,池中还有多少水
(3)几小时后,池中还有200立方米的水
解析 (1)Q=800-50t(0≤t≤16).
(2)当t=6时,Q=800-50×6=500(立方米).
(3)当Q=200时,800-50t=200,解得t=12.
所以12小时后,池中还有200立方米的水.
6.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(1)在这个变化中,自变量和因变量各
是什么?
(2)写出圆柱的体积V与高h之间的关系式.
自变量是圆柱的高,因变量是圆柱的体积.
V= =πh.
7.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(3)当h由10 cm变化到5 cm时,V是怎样变化的?
(4)当h=0时,V等于多少?此时表示什么?
当h=10cm时,V=πh=10πcm3;
当h=5cm时,V=πh=5πcm3.
所以当h由10cm变化到5cm时,
V从10πcm3变化到5πcm3.
V=0,此时表示平面图形——直径为2cm的圆.
8.对于气温,有的地方用摄氏温度表
示,有的地方用华氏温度表示,摄氏
温度x(℃)与华氏温度y(°F)之间存在
的关系为:y=1.8x+32,如图所示:
(1)用表格表示当x从-10到30(每次增加10),y的相
应的值.
解:(1)
(2)某天,连云港的最高气温是8℃,悉尼的最高气
温是91°F,问这一天悉尼的最高气温比连云港
的最高气温高多少摄氏度(结果保留整数)?
解:(2)y=91,则1.8x+32=91,
所以有x≈33,
33-8=25(℃).
所以这一天悉尼的最高气温比连云港的高25℃.
求变量之间关系式的“三途径”
1.根据表格中所列的数据,归纳总结两个变量的关
系式.
2.利用公式写出两个变量之间的关系式,比如各类
几何图形的周长、面积、体积公式等.
3.结合实际问题写出两个变量之间的关系式,比如
销量×(售价-进价)=利润等.
课堂小结
https://www.21cnjy.com/help/help_extract.php
北师大版七年级下册数学
第三章 变量之间的关系
3.2用关系式表示的变量间关系
游戏:数青蛙
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿;
……
1.青蛙的眼睛数和只数有关系吗?能用数学式表达吗?
2.青蛙的腿数和只数有关系吗?能用数学式表达吗?
这个游戏你能继续玩下去吗?
情景引入
探究活动1 变化的三角形
y=3x
36
9
三角形的底边长度是自变量; 三角形的面积是因变量
探究活动1 变化的三角形
36 33 30 27 24 21 18 15 12 9
关系式是我们表示变量之间关系的另一种方法,利用关系式(如y=3x),我们可以根据任何一个自变量值求出相应的因变量的值.
y=3x表示了三角形底边长x和三角形面积y之间的关系,它是变量y随x变化的关系式.
探究活动1 变化的三角形
2.归纳总结
探究活动2 表格和关系式对比
1.两种表示变量关系的方法有什么异同.
2.归纳总结
(2)关系式是我们表示变量之间关系的另一种方法.
(1) y=3x表示了上图中三角形底边长 x 和面积 y 之
间的关系,它是因变量 y 随自变量 x 变化的关系式.
探究活动2 表格和关系式对比
2.归纳总结
(3)关系式法的优点:
利用表格表示的变量间关系虽能直观地知道因变量
和自变量间的对应关系,但是不够全面,不能找出对于
任意一个自变量的值所对应的因变量的值.
自变量为圆锥的底面半径,
因变量为圆锥的体积
1.用来表示自变量和因变量之间关系的等式叫做关系式
要点精析:
关系式的基本特征是:
①等式的左边是因变量,等式的右边是关于自变
量的代数式;
②等式中只含有自变量和因变量这两个变量,其
他的量都是常量;
③自变量可在允许的范围内任意取值.
小结
2.求两个变量之间的关系式常用的方法:
(1)利用公式:如图形的周长公式、面积公式、体积公
式等;
(2)利用生活中特定的数量 关系,如行程问题中“路
程=时间×速度”,销售问题中“销售额=单价×
数量”等;
(3)根据表格与图象中的信息列关系式(这种方法以后
会学习)等.
例1
长方形的周长为24 cm,其中一边长为x cm(x>0),面积为y cm2,则该长方形中y与x的关系可以写为
( )
A.y=x2 B.y=(12-x)2
C.y=(12-x)·x D.y=2(12-x)
因为长方形的周长为24 cm,其中一边长为x cm,
所以另一边长为(12-x) cm,因为面积为y cm2,
所以该长方形中y与x的关系可以写为y=(12-x)·x.
导引:
C
典型例题
例2
百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其销售量x(米)与售价y(元)如下表:
下列用销售量x(米)表示售价y(元)的关系式中,正确的是
( )
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
通过观察表格内x与y的关系,可知y的值相对于x=1时是
成倍增长的,由此可得y=(8+0.3)x.
导引:
销售量x/米 1 2 3 4 …
售价y/元 8+0.3 16+0.6 24+0.9 32+1.2 …
B
议一议
你知道什么是“低碳生活”吗? “低碳生活”
是指人们生活中尽量减少所耗能量,从而降低碳(特
别是二氧化碳)的排放量的一种生活方式.
用关系式求值
y = 0.785x
y 表示二氧化碳的排放量(kg),
x 表示的是耗电量(kW·h)
0.785 kg
0.785 kg
78.5 kg
提示:根据上面的排碳计算公式,
用电排放的二氧化碳数量为0.785×110=86.35(kg);
用天然气排放的二氧化碳数量为20×0.19=3.8(kg);
用自来水排放的二氧化碳数量为5×0.91=4.55(kg);
开私家车耗油排放的二氧化碳数量为75×2.7=202.5(kg).
以上各项相加得297.2 kg.
即小明家这几项的二氧化碳排放量为297.2 kg
例3
某工厂现在年产值是15万元,计划今后每年增加2
万元.
(1)年产值y(万元)与年数x之间的关系式为 __________;
(2)5年后的年产值是______万元.
(1)根据题意可知,现在年产值是15万元,计划今后
每年增加2万元,x年后增加2x万元,所以年产值
y(万元)与年数x之间的关系式为y=2x+15;
(2)将x=5代入关系式得:y=2x+15=2×5+15=25.
导引:
y=2x+15
25
典型例题
1.变量x与y之间的关系式是y=x2-3,当自变量x=2
时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
C
【解析】将x=2代入y=x2-3,得y=22-3=1.
课堂练习
2.一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为( )
A.y=2x B.y=10-2x
C.y=5x D.y=10-5x
【解析】由题意,有y=2(5-x),即y=10-2x.
B
3.如图是一个简单的数值运算程序,当输入x的值
为1时,则输出的数值为____.
【解析】根据程序,计算过程可以表示为:-x+3,
所以当x=1时,原式=-1+3=2.
4.在关系式S=40t中,当t=1.5时,S=____.
【解析】把t=1.5代入S=40t中,得S=40×1.5=60.
60
2
5.已知水池中有800立方米的水,每小时抽50立方米.
(1)写出剩余水的体积Q(立方米)与时间t(小时)之间的关系式;
(2)6小时后,池中还有多少水
(3)几小时后,池中还有200立方米的水
解析 (1)Q=800-50t(0≤t≤16).
(2)当t=6时,Q=800-50×6=500(立方米).
(3)当Q=200时,800-50t=200,解得t=12.
所以12小时后,池中还有200立方米的水.
6.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(1)在这个变化中,自变量和因变量各
是什么?
(2)写出圆柱的体积V与高h之间的关系式.
自变量是圆柱的高,因变量是圆柱的体积.
V= =πh.
7.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(3)当h由10 cm变化到5 cm时,V是怎样变化的?
(4)当h=0时,V等于多少?此时表示什么?
当h=10cm时,V=πh=10πcm3;
当h=5cm时,V=πh=5πcm3.
所以当h由10cm变化到5cm时,
V从10πcm3变化到5πcm3.
V=0,此时表示平面图形——直径为2cm的圆.
8.对于气温,有的地方用摄氏温度表
示,有的地方用华氏温度表示,摄氏
温度x(℃)与华氏温度y(°F)之间存在
的关系为:y=1.8x+32,如图所示:
(1)用表格表示当x从-10到30(每次增加10),y的相
应的值.
解:(1)
(2)某天,连云港的最高气温是8℃,悉尼的最高气
温是91°F,问这一天悉尼的最高气温比连云港
的最高气温高多少摄氏度(结果保留整数)?
解:(2)y=91,则1.8x+32=91,
所以有x≈33,
33-8=25(℃).
所以这一天悉尼的最高气温比连云港的高25℃.
求变量之间关系式的“三途径”
1.根据表格中所列的数据,归纳总结两个变量的关
系式.
2.利用公式写出两个变量之间的关系式,比如各类
几何图形的周长、面积、体积公式等.
3.结合实际问题写出两个变量之间的关系式,比如
销量×(售价-进价)=利润等.
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
