2021-2022学年冀教版数学八年级下册20.2.1函数 同步课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年冀教版数学八年级下册20.2.1函数 同步课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第二十章 函数
20.2 函数
第1课时 函数的概念
“早穿皮袄午穿纱”
说明__________随_________的
变化而变化.
“高处不胜寒”
说明_________随__________的
变化而变化.
高度
气温
时间
气温
创设情景
新课导入
问题1
思考并解决下列问题:
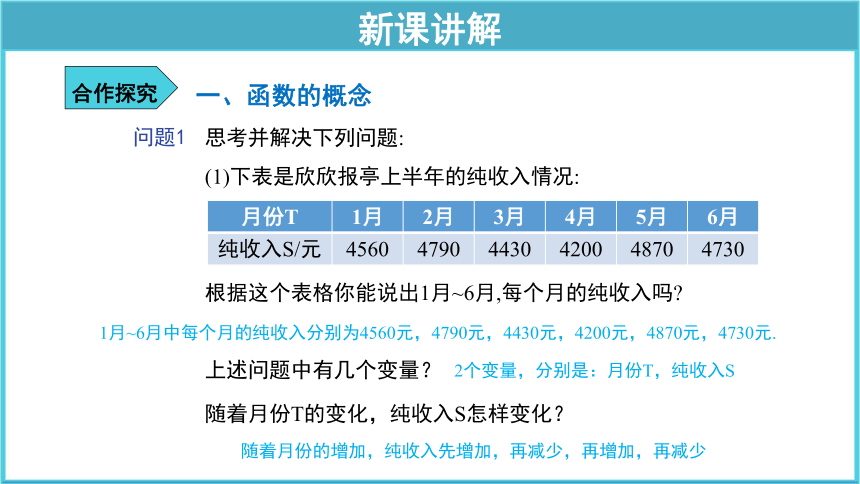
(1)下表是欣欣报亭上半年的纯收入情况:
根据这个表格你能说出1月~6月,每个月的纯收入吗
月份T 1月 2月 3月 4月 5月 6月
纯收入S/元 4560 4790 4430 4200 4870 4730
1月~6月中每个月的纯收入分别为4560元,4790元,4430元,4200元,4870元,4730元.
新课讲解
合作探究
一、函数的概念
上述问题中有几个变量?
随着月份T的变化,纯收入S怎样变化?
2个变量,分别是:月份T,纯收入S
随着月份的增加,纯收入先增加,再减少,再增加,再减少
问题1
思考并解决下列问题:
新课讲解
一、函数的概念
(2)如图所示的是某市冬季某天的气温变化图.观察这个气温变化图,你能找到凌晨3时、上午9时和下午16时对应的温度吗 你能得到这天24小时内任意时刻对应的温度吗
凌晨3时、上午9时和下午16时对应的温度分别是:-3℃,1℃,4℃;
上述问题中有几个变量?
随着时间t的变化,温度T怎样变化?
能
2个变量,分别是:时间t、温度T
凌晨0时-凌晨3时、下午14时-凌晨24时,温度随时间的增加而降低;
凌晨3时-下午14时,温度随时间的增加而升高;
合作探究
问题1
思考并解决下列问题:
新课讲解
一、函数的概念
(3)我们曾做过“对折纸”的游戏:取一张纸,第1次对折,1页纸折为2层;第2次对折,2层纸折为4层;第3次对折,4层纸折为8层……用n表示对折的次数,p表示对折后的层数,请写出用n表示p的表达式.根据写出的表达式,是否可以得出任意次对折后的层数
p=2n.
可以得出任意次对折后的层数
上述问题中有几个变量?
随着对折次数n的变化,对折后的层数p怎样变化?
2个变量,分别是:对折次数n、对折后的层数p
对折后的层数p随着对折次数n的增加而增加
合作探究
新课讲解
一、函数的概念
三个实例中的两个变量之间分别具有相互依赖关系,
当其中一个变量变化时,另一个变量也相应地变化,
并且当其中一个变量取定一个值时,另一个变量也相应地取定一个值.
问题2
在上述三个问题中, 试说明在同一个问题中:
当其中一个量变化时,另一个量是否也在相应地变化;
当其中一个量取定一个值时,另一个量是否也相应地取定一个值.
合作探究
新课讲解
一般地,在某个变化过程中,有两个变量x和y.如果给定x的一个值,就能相应地确定y的一个值,那么,我们就说y是x的函数.其中,x叫做自变量.
y与x具有函数关系
新课讲解
欣欣报亭上半年的纯收入S(元)是月份T的函数,T是自变量;
(2)
某市某一天的气温T(℃)是时刻t的函数,t是自变量;
(3)折纸游戏中,折纸次数n与折纸的层数p满足关系:p=2n.
折纸的层数p是折纸次数n的函数,n是自变量.
你能说出前面问题1(1)~(3)中的函数和自变量吗?
1.如果y是x的函数,那么哪个量是自变量,哪个量是自变量的函数
想一想
2.在上面的问题中,我们认识了用“数值表、图像、表达式”三种方式分别表示的函数,请你再用这三种方式各举一个表示函数关系的例子.
x是自变量、 y是自变量x的函数
x 1 2 3 4 5
y 12 24 36 48 60
y=3x+1
新课讲解
例1:改革开放以来,我国城乡居民的生活发生了巨大变化.下表是国家统计局公布的近几年人民币储蓄存款余额的情况:
在这里,存款余额(亿元)与年份两个量之间是否具有函数关系 若具有函数关系,请指出其中的自变量和关于自变量的函数.
年 份 2005 2006 2007 2008 2009 2010
存款余额/亿元 141 051 161 587 172 534 217 885 260 772 303 302
存款余额与年份具有函数关系,
年份是自变量,存款余额是年份的函数.
例题讲解
新课讲解
例2:海水受日月的引力而产生潮汐现象.海水早晨上涨的现象叫做潮,黄昏上涨的现象叫做汐,潮与汐合称潮汐.某港口的某一天,从0时至24时的水位情况如图所示.变量h与变量t是否具有函数关系 若具有函数关系,则哪个量是自变量,哪个量是这个自变量的函数
例题讲解
h与t具有函数关系,t是自变量,h是t的函数.
新课讲解
练一练
下列关于变量x,y的关系中,y不是x的函数的是( )
D
x 1 2 3 4
y 2 4 6 8
x -3 0 3
y 9 0 9
x 1 2 3 4
y -1 -2 -3 -4
x 1 4
y ±1 ±2
A.
C.
B.
D.
归纳总结
函数不是数,函数的本质是对应,函数关系就是变量之间的对应关系,且是一种特殊的对应关系,必须是“对于x的每一个值,y都有唯一的值和它对应”.
新课讲解
√
√
√
×
课堂练习
1.下列各曲线中表示y是x的函数的是( )
D
√
×
×
×
课堂练习
2. 下列说法正确的是 ( )
A.若y<2x,则y是x的函数
B.正方形的面积是其周长的函数
C.变量x,y满足y2=2x,y是x的函数
D.温度是变量
D
√
×
S=( )2
×
当x=2时,y=±2
×
视情况而定,如:在科学实验时,可以控制温度固定不变.
课堂练习
3.已知△ABC的底边BC上的高为8 cm,当它的底边BC从16 cm变化到5 cm时,△ABC的面积( )
A.从20 cm2变化到64 cm2 B.从64 cm2变化到20 cm2
C.从128 cm2变化到40 cm2 D.从40 cm2变化到128 cm2
B
当底边BC=16cm时;
当高为定值时,面积随底边的减小而减小
= ×16×8=64cm2
当底边BC=5cm时;
= ×5×8=20cm2
函 数
一般地,在某个变化过程中,有两个变量x和y.如果给定x的一个值,就能相应地确定y的一个值,那么,我们就说y是x的函数.其中,x叫做自变量.
对于函数的理解:
(1)在某一个变化过程中有两个变量;
(2)一个变量的数值随着另一个变量的数值的变化而发生变化;
(3)自变量的每一个确定的值,函数有且只有一个值与之对应,即单对应.
课堂小结
再 见
第二十章 函数
20.2 函数
第1课时 函数的概念
“早穿皮袄午穿纱”
说明__________随_________的
变化而变化.
“高处不胜寒”
说明_________随__________的
变化而变化.
高度
气温
时间
气温
创设情景
新课导入
问题1
思考并解决下列问题:
(1)下表是欣欣报亭上半年的纯收入情况:
根据这个表格你能说出1月~6月,每个月的纯收入吗
月份T 1月 2月 3月 4月 5月 6月
纯收入S/元 4560 4790 4430 4200 4870 4730
1月~6月中每个月的纯收入分别为4560元,4790元,4430元,4200元,4870元,4730元.
新课讲解
合作探究
一、函数的概念
上述问题中有几个变量?
随着月份T的变化,纯收入S怎样变化?
2个变量,分别是:月份T,纯收入S
随着月份的增加,纯收入先增加,再减少,再增加,再减少
问题1
思考并解决下列问题:
新课讲解
一、函数的概念
(2)如图所示的是某市冬季某天的气温变化图.观察这个气温变化图,你能找到凌晨3时、上午9时和下午16时对应的温度吗 你能得到这天24小时内任意时刻对应的温度吗
凌晨3时、上午9时和下午16时对应的温度分别是:-3℃,1℃,4℃;
上述问题中有几个变量?
随着时间t的变化,温度T怎样变化?
能
2个变量,分别是:时间t、温度T
凌晨0时-凌晨3时、下午14时-凌晨24时,温度随时间的增加而降低;
凌晨3时-下午14时,温度随时间的增加而升高;
合作探究
问题1
思考并解决下列问题:
新课讲解
一、函数的概念
(3)我们曾做过“对折纸”的游戏:取一张纸,第1次对折,1页纸折为2层;第2次对折,2层纸折为4层;第3次对折,4层纸折为8层……用n表示对折的次数,p表示对折后的层数,请写出用n表示p的表达式.根据写出的表达式,是否可以得出任意次对折后的层数
p=2n.
可以得出任意次对折后的层数
上述问题中有几个变量?
随着对折次数n的变化,对折后的层数p怎样变化?
2个变量,分别是:对折次数n、对折后的层数p
对折后的层数p随着对折次数n的增加而增加
合作探究
新课讲解
一、函数的概念
三个实例中的两个变量之间分别具有相互依赖关系,
当其中一个变量变化时,另一个变量也相应地变化,
并且当其中一个变量取定一个值时,另一个变量也相应地取定一个值.
问题2
在上述三个问题中, 试说明在同一个问题中:
当其中一个量变化时,另一个量是否也在相应地变化;
当其中一个量取定一个值时,另一个量是否也相应地取定一个值.
合作探究
新课讲解
一般地,在某个变化过程中,有两个变量x和y.如果给定x的一个值,就能相应地确定y的一个值,那么,我们就说y是x的函数.其中,x叫做自变量.
y与x具有函数关系
新课讲解
欣欣报亭上半年的纯收入S(元)是月份T的函数,T是自变量;
(2)
某市某一天的气温T(℃)是时刻t的函数,t是自变量;
(3)折纸游戏中,折纸次数n与折纸的层数p满足关系:p=2n.
折纸的层数p是折纸次数n的函数,n是自变量.
你能说出前面问题1(1)~(3)中的函数和自变量吗?
1.如果y是x的函数,那么哪个量是自变量,哪个量是自变量的函数
想一想
2.在上面的问题中,我们认识了用“数值表、图像、表达式”三种方式分别表示的函数,请你再用这三种方式各举一个表示函数关系的例子.
x是自变量、 y是自变量x的函数
x 1 2 3 4 5
y 12 24 36 48 60
y=3x+1
新课讲解
例1:改革开放以来,我国城乡居民的生活发生了巨大变化.下表是国家统计局公布的近几年人民币储蓄存款余额的情况:
在这里,存款余额(亿元)与年份两个量之间是否具有函数关系 若具有函数关系,请指出其中的自变量和关于自变量的函数.
年 份 2005 2006 2007 2008 2009 2010
存款余额/亿元 141 051 161 587 172 534 217 885 260 772 303 302
存款余额与年份具有函数关系,
年份是自变量,存款余额是年份的函数.
例题讲解
新课讲解
例2:海水受日月的引力而产生潮汐现象.海水早晨上涨的现象叫做潮,黄昏上涨的现象叫做汐,潮与汐合称潮汐.某港口的某一天,从0时至24时的水位情况如图所示.变量h与变量t是否具有函数关系 若具有函数关系,则哪个量是自变量,哪个量是这个自变量的函数
例题讲解
h与t具有函数关系,t是自变量,h是t的函数.
新课讲解
练一练
下列关于变量x,y的关系中,y不是x的函数的是( )
D
x 1 2 3 4
y 2 4 6 8
x -3 0 3
y 9 0 9
x 1 2 3 4
y -1 -2 -3 -4
x 1 4
y ±1 ±2
A.
C.
B.
D.
归纳总结
函数不是数,函数的本质是对应,函数关系就是变量之间的对应关系,且是一种特殊的对应关系,必须是“对于x的每一个值,y都有唯一的值和它对应”.
新课讲解
√
√
√
×
课堂练习
1.下列各曲线中表示y是x的函数的是( )
D
√
×
×
×
课堂练习
2. 下列说法正确的是 ( )
A.若y<2x,则y是x的函数
B.正方形的面积是其周长的函数
C.变量x,y满足y2=2x,y是x的函数
D.温度是变量
D
√
×
S=( )2
×
当x=2时,y=±2
×
视情况而定,如:在科学实验时,可以控制温度固定不变.
课堂练习
3.已知△ABC的底边BC上的高为8 cm,当它的底边BC从16 cm变化到5 cm时,△ABC的面积( )
A.从20 cm2变化到64 cm2 B.从64 cm2变化到20 cm2
C.从128 cm2变化到40 cm2 D.从40 cm2变化到128 cm2
B
当底边BC=16cm时;
当高为定值时,面积随底边的减小而减小
= ×16×8=64cm2
当底边BC=5cm时;
= ×5×8=20cm2
函 数
一般地,在某个变化过程中,有两个变量x和y.如果给定x的一个值,就能相应地确定y的一个值,那么,我们就说y是x的函数.其中,x叫做自变量.
对于函数的理解:
(1)在某一个变化过程中有两个变量;
(2)一个变量的数值随着另一个变量的数值的变化而发生变化;
(3)自变量的每一个确定的值,函数有且只有一个值与之对应,即单对应.
课堂小结
再 见
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
