2.2.1直线与平面平行的判定
文档属性
| 名称 | 2.2.1直线与平面平行的判定 |  | |
| 格式 | zip | ||
| 文件大小 | 121.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-10 22:01:26 | ||
图片预览


文档简介
课件17张PPT。2.2.1直线与平面平行的判定湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作
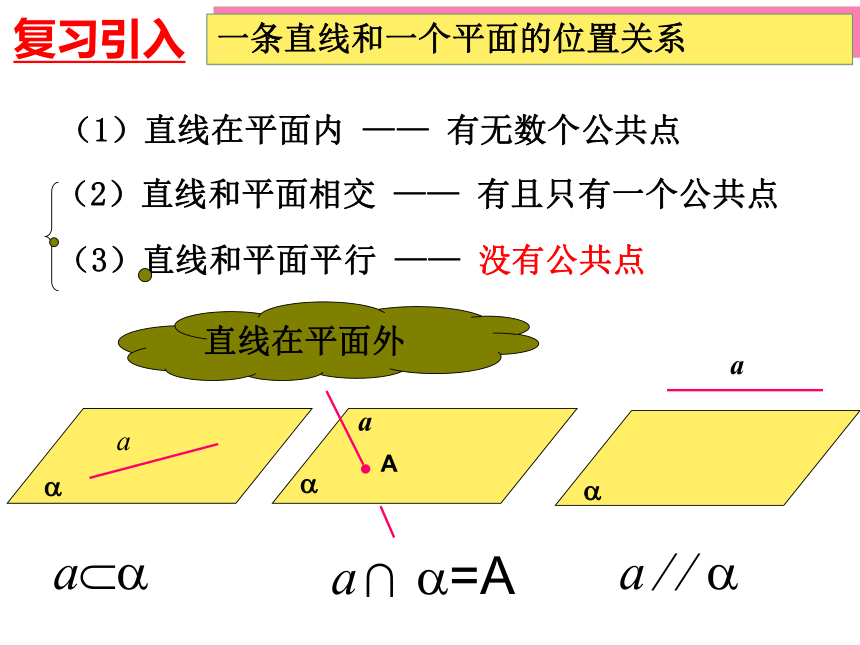
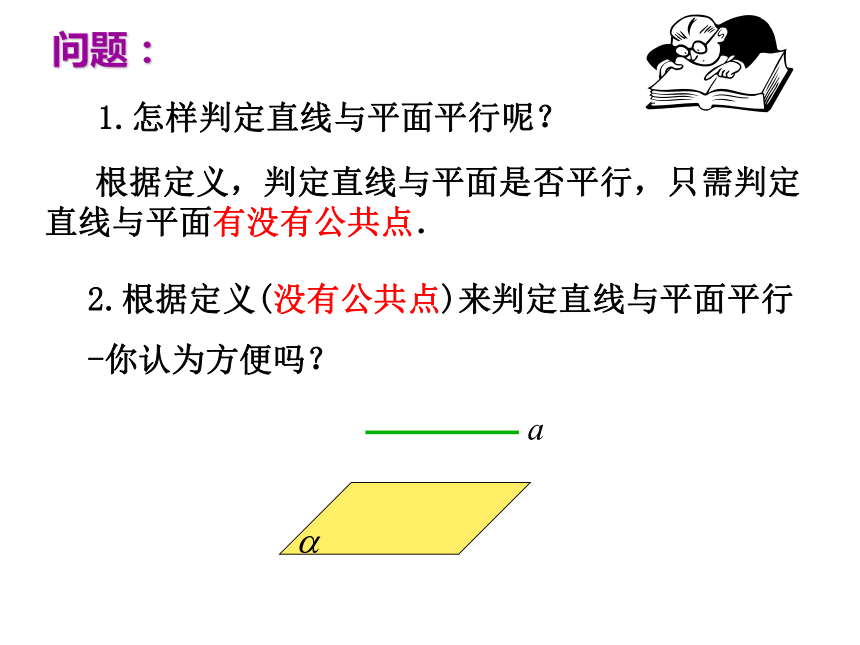
2012.12. 2一条直线和一个平面的位置关系(1)直线在平面内 —— 有无数个公共点 (2)直线和平面相交 —— 有且只有一个公共点 (3)直线和平面平行 —— 没有公共点 a??a ? ? ?复习引入a ?=A 1.怎样判定直线与平面平行呢?问题: 根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.2.根据定义(没有公共点)来判定直线与平面平行-你认为方便吗?
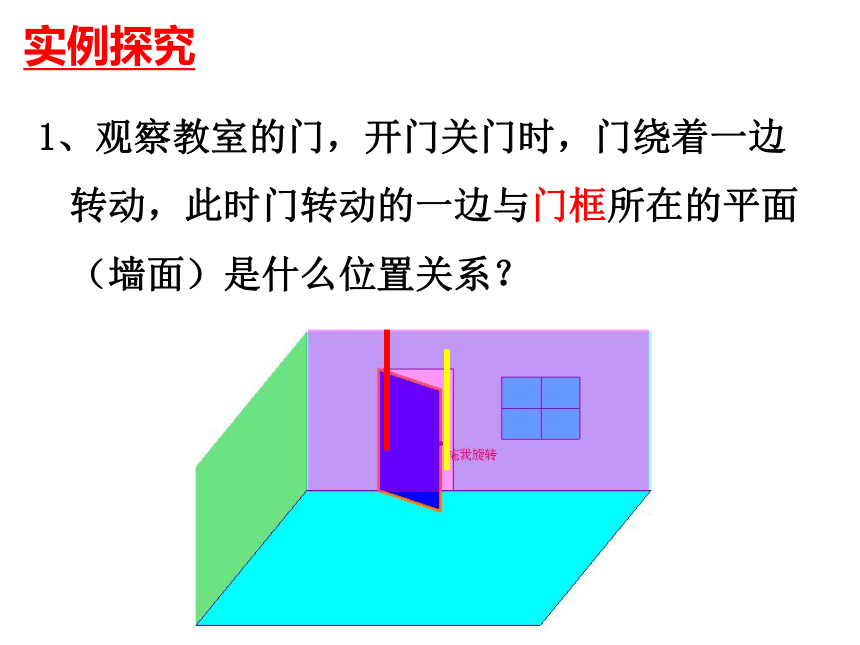
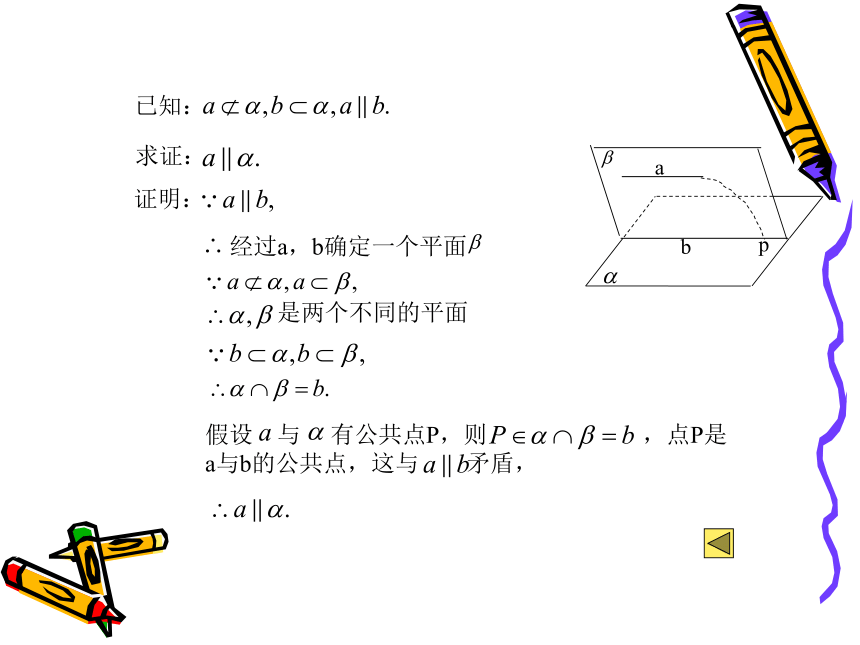
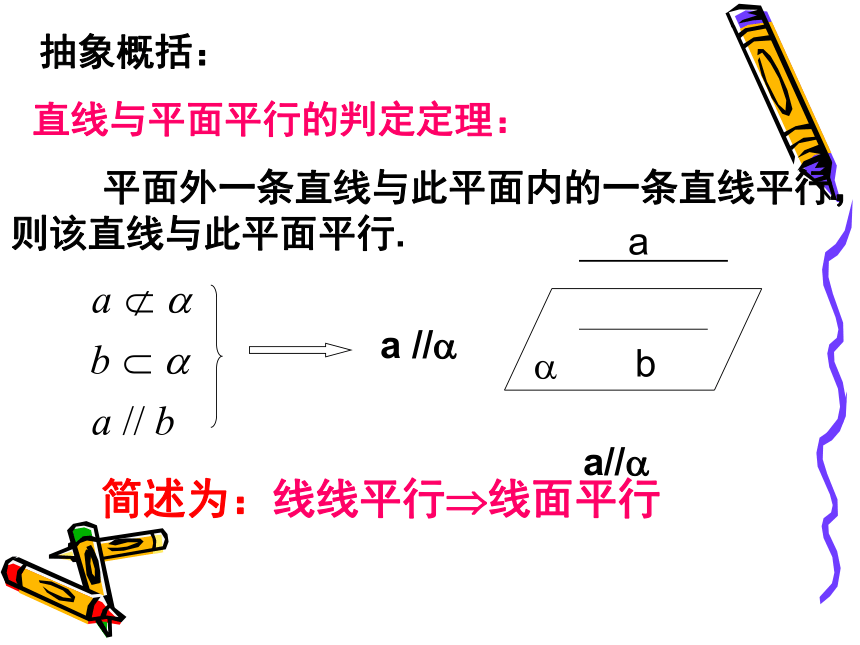
1、观察教室的门,开门关门时,门绕着一边转动,此时门转动的一边与门框所在的平面(墙面)是什么位置关系?实例探究2、将一本书平放在桌面上,翻动书的书页,观察书页边缘所在直线与桌面所在的平面具有怎样的位置关系?已知:求证:证明:经过a,b确定一个平面是两个不同的平面假设 与 有公共点P,则 ,点P是a与b的公共点,这与 矛盾,abp抽象概括:直线与平面平行的判定定理: 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.简述为:线线平行?线面平行温馨提示:
作用:判定或证明线面平行。
关键:在平面内找(或作)出一条直线与
面外的直线平行。
思想:线线平行?线面平行
(空间问题?平面问题)1、填空:b ∥ α,b与 α相交
巩固练习2、判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例
(1)如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;(2)如果直线a和平面α 满足a∥平面α ,那么a 与平面α内的任何直线平行(3)如果直线a、b和平面α 满足a ∥ α,b ∥ α,那么a ∥ b ;(4)如果直线a、b和平面α 满足a ∥ b,a ∥ α,b α,
那么 b ∥ α;(5)过平面外一点和这个平面平行的直线只有一条典型例题讲解 例1、求证:空间四边形相邻两边中点的连线,平行于经过另两边的平面。已知:空间四边形ABCD中,E、F分别是AB、AD的中点。
求证:EF ∥ 平面BCD
分析:EF在面BCD外,要证明EF∥面BCD,只要证明EF和面BCD内一条直线平行即可。EF和面BCD哪一条直线平行呢?连结BD立刻就清楚了。 1.在平面内寻求一条与已知直线可能具有平行关系的直线;2.证明两条直线平行;3.由判定定理得出结论。总结证明线面平行的一般步骤: 补充例题 在长方体ABCD—A1B1C1D1中.
(1)作出过直线AC且与直线BD1平行的
截面,并说明理由.
(2)设E,F分别是A1B和B1C的中点,
求证直线EF//平面ABCD.1、已知四棱锥S-ABCD,ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点.
求证:SA//平面MDBSMCDBA课堂练习2、已知E、F分别为正方体ABCD-A1B1C1D1棱BC、C1D1的中点,求证:EF ∥平面BB1DD1D证明:取BD中点O,则OE
为△ BDC 的中位线
∴D1OEF为平行四边形∴EF ∥D1O∴ EF ∥平面BB1DD1 EFO(1)线面平行的判定定理线线平行线面平行(空间问题?平面问题)(2)线面平行的判定方法;平行移动法注意六个字:
(1)面外
(2)面内 (3)平行关键是找平行课堂小结课后作业P55练习:1.
P62习题2.2A组:3,4.
高中数学老师欧阳文丰制作
2012.12. 2一条直线和一个平面的位置关系(1)直线在平面内 —— 有无数个公共点 (2)直线和平面相交 —— 有且只有一个公共点 (3)直线和平面平行 —— 没有公共点 a??a ? ? ?复习引入a ?=A 1.怎样判定直线与平面平行呢?问题: 根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.2.根据定义(没有公共点)来判定直线与平面平行-你认为方便吗?
1、观察教室的门,开门关门时,门绕着一边转动,此时门转动的一边与门框所在的平面(墙面)是什么位置关系?实例探究2、将一本书平放在桌面上,翻动书的书页,观察书页边缘所在直线与桌面所在的平面具有怎样的位置关系?已知:求证:证明:经过a,b确定一个平面是两个不同的平面假设 与 有公共点P,则 ,点P是a与b的公共点,这与 矛盾,abp抽象概括:直线与平面平行的判定定理: 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.简述为:线线平行?线面平行温馨提示:
作用:判定或证明线面平行。
关键:在平面内找(或作)出一条直线与
面外的直线平行。
思想:线线平行?线面平行
(空间问题?平面问题)1、填空:b ∥ α,b与 α相交
巩固练习2、判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例
(1)如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;(2)如果直线a和平面α 满足a∥平面α ,那么a 与平面α内的任何直线平行(3)如果直线a、b和平面α 满足a ∥ α,b ∥ α,那么a ∥ b ;(4)如果直线a、b和平面α 满足a ∥ b,a ∥ α,b α,
那么 b ∥ α;(5)过平面外一点和这个平面平行的直线只有一条典型例题讲解 例1、求证:空间四边形相邻两边中点的连线,平行于经过另两边的平面。已知:空间四边形ABCD中,E、F分别是AB、AD的中点。
求证:EF ∥ 平面BCD
分析:EF在面BCD外,要证明EF∥面BCD,只要证明EF和面BCD内一条直线平行即可。EF和面BCD哪一条直线平行呢?连结BD立刻就清楚了。 1.在平面内寻求一条与已知直线可能具有平行关系的直线;2.证明两条直线平行;3.由判定定理得出结论。总结证明线面平行的一般步骤: 补充例题 在长方体ABCD—A1B1C1D1中.
(1)作出过直线AC且与直线BD1平行的
截面,并说明理由.
(2)设E,F分别是A1B和B1C的中点,
求证直线EF//平面ABCD.1、已知四棱锥S-ABCD,ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点.
求证:SA//平面MDBSMCDBA课堂练习2、已知E、F分别为正方体ABCD-A1B1C1D1棱BC、C1D1的中点,求证:EF ∥平面BB1DD1D证明:取BD中点O,则OE
为△ BDC 的中位线
∴D1OEF为平行四边形∴EF ∥D1O∴ EF ∥平面BB1DD1 EFO(1)线面平行的判定定理线线平行线面平行(空间问题?平面问题)(2)线面平行的判定方法;平行移动法注意六个字:
(1)面外
(2)面内 (3)平行关键是找平行课堂小结课后作业P55练习:1.
P62习题2.2A组:3,4.
