2.2.2《平面与平面平行的判定》课件(新人教版A必修2)
文档属性
| 名称 | 2.2.2《平面与平面平行的判定》课件(新人教版A必修2) |  | |
| 格式 | zip | ||
| 文件大小 | 761.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-10 22:04:36 | ||
图片预览





文档简介
课件23张PPT。平面与平面平行的判定 湖南省耒阳市振兴学校
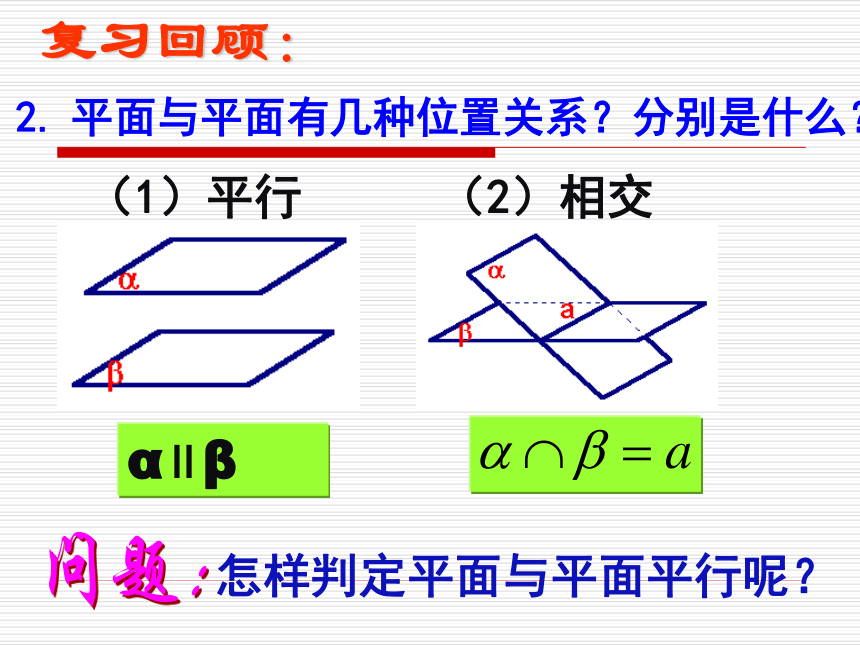
高中数学老师欧阳文丰制作复习回顾: 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.(2)直线与平面平行的判定定理:(1)定义法: 1.?到现在为止,我们一共学习过几种判断直线与平面平行的方法呢?(1)平行(2)相交α∥β复习回顾:怎样判定平面与平面平行呢?问题:2.?平面与平面有几种位置关系?分别是什么?生活中有没有平面与平面平行的例子呢?(1)三角板或课本的一条边所在直线与桌面平行,这个三角板或课本所在平面与桌面平行吗?
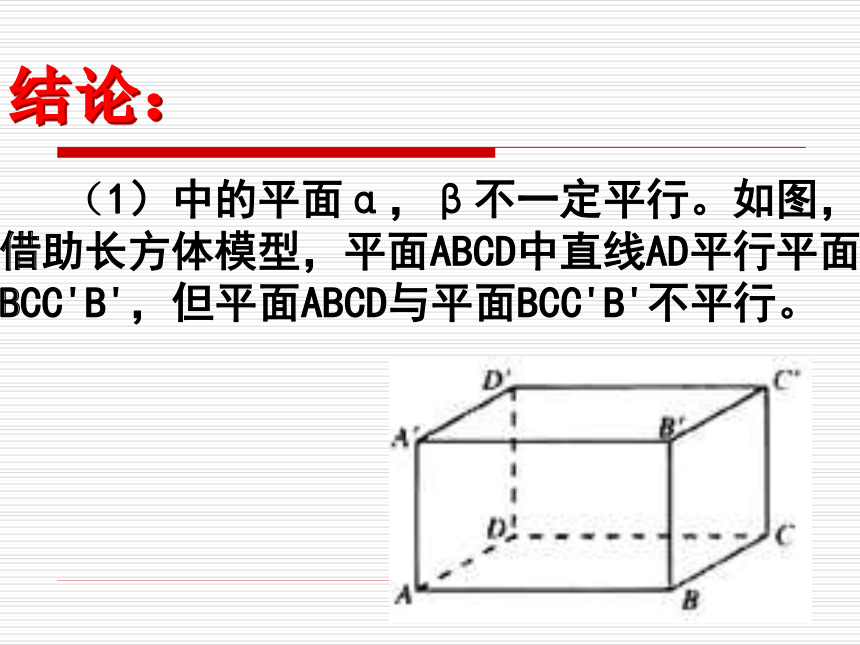
(2)三角板或课本的两条边所在直线分别与桌面平行,情况又如何呢?观察:思考: 教室的天花板与地面给人平行的感觉,前后两块黑板也是平行的。探究:当三角板的两条边所在直线分别与地面平行时,这个三角板所在平面与地面平行。结论:(1)平面?内有一条直线与平面?平行,?,?平行吗?结论: (1)中的平面α,β不一定平行。如图,借助长方体模型,平面ABCD中直线AD平行平面BCC'B',但平面ABCD与平面BCC'B'不平行。 (2)平面?内有两条直线与平面?
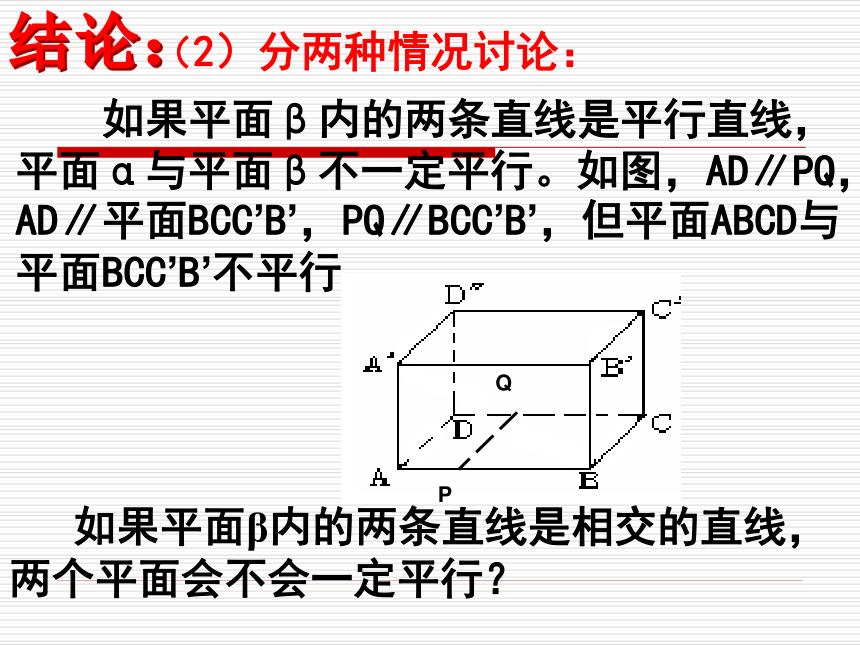
平行,?,?平行吗?探究:结论:(2)分两种情况讨论: 如果平面β内的两条直线是平行直线,
平面α与平面β不一定平行。如图,AD∥PQ,AD∥平面BCC’B’,PQ∥BCC’B’,但平面ABCD与
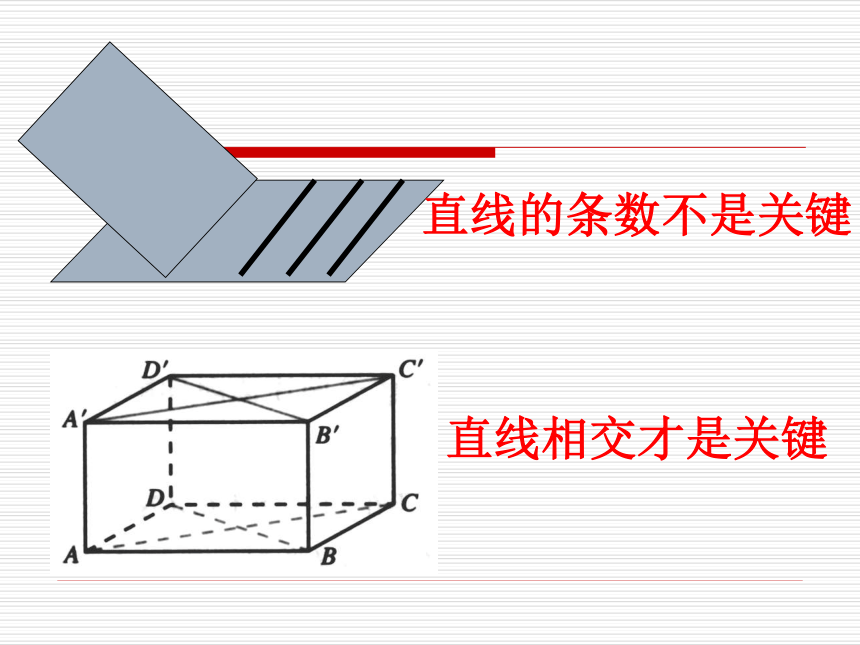
平面BCC’B’不平行。 如果平面β内的两条直线是相交的直线,两个平面会不会一定平行?直线的条数不是关键直线相交才是关键 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行 两个平面平行的判定定理:线不在多,重在相交符号表示: a??,b??,
a?b=P,
a???,b???图形表示:结论:?????线面平行 面面平行线线平行两个平面平行的判定定理的证明已知:在平面内 ,有两条直线 、 相交且和平面 平行. 求证: . 证明:用反证法证明. 假设 . 同理这与题设 和 是相交直线是矛盾的.推论1:如果一个平面内有两条相交直线分别平行与另一个平面内的两条直线,那么这两个平面平行。推论2:平行于同一个平面的两个平面平行。基础尝试性练习判断下列命题是否正确:
( )1、如果一个平面内有两条直线平行于另一个
平面,那么这两个平面平行;
( ) 2、如果一个平面内有两条不平行的直线都平
行于另一个平面,那么这两个平面平行;
( )3、如果一个平面内有无数条直线分别平行于
另一个平面,那么这两个平面平行;
( )4、如果一个平面内任意一条直线都平行于另
一个平面,那么这两个平面平行. 例1:已知正方体ABCD-A1B1C1D1,求证:平面AB1D1//平面C1BD证明:因为ABCD-A1B1C1D1为正方体,
所以 D1C1∥A1B1,D1C1=A1B1
又AB∥A1B1,AB=A1B1,
∴D1C1∥AB,D1C1=AB,
∴D1C1BA是平行四边形,
∴D1A∥C1B,又D1A 平面C1BD,
CB 平面C1BD.由直线与平面平行的判定,可知同理??D1B1∥平面C1BD,又 D1A∩D1B1=D1,所以,平面AB1D1∥平面C1BD。D1A∥平面C1BD,
2.寻找平行直线可以通过三角形的中位线、梯形的中位线、平行线的判定等来完成。反思~领悟:1. 线线平行 线面平行 面面平行来处理。 变式:在正方体ABCD-A1B1C1D1中,
若 M、N、E、F分别是棱A1B1,A1D1,B1C1,
C1D1的中点,求证:平面AMN//平面EFDB。ABCA1B1C1D1DMNEF∴MN∥B1D1 B1D1∥EF∴MN∥EFMN∥平面BDFEMF∥A1D1, A1D1∥AD∴MF∥AD且MF=A1D1= ADAM ∥DF∴ AM∥平面DBEF∴平面AMN∥平面EFDB 如图:三棱锥P-ABC, D,E,F分别是棱PA,PB,PC中点,
求证:平面DEF∥平面ABC。PDEFABC补充例题NMFEDCBAH1 如图所示,平面ABCD∩平面EFCD = CD,
M、N、H 分别是 DC、CF、CB 的中点,
求证 平面 MNH // 平面 DBF课堂练习 2、已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD的中点PQR求证:PQ∥平面BCE。思路1:在平面BCE内找PQ平行线。思路2:过PQ构造与平面BCE平行的平面。课堂总结:1、面面平行的定义;2、面面平行的判定定理;3、面面平行判定定理的应用:要证面面平行,只要证线面平行,而要证线面平行,只要证线线平行。在立体几何中,往往通过线线、线面、面面间的位置关系的转化使问题得到解决。作业布置:
第62页习题2.2?A组第7,8题。
高中数学老师欧阳文丰制作复习回顾: 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.(2)直线与平面平行的判定定理:(1)定义法: 1.?到现在为止,我们一共学习过几种判断直线与平面平行的方法呢?(1)平行(2)相交α∥β复习回顾:怎样判定平面与平面平行呢?问题:2.?平面与平面有几种位置关系?分别是什么?生活中有没有平面与平面平行的例子呢?(1)三角板或课本的一条边所在直线与桌面平行,这个三角板或课本所在平面与桌面平行吗?
(2)三角板或课本的两条边所在直线分别与桌面平行,情况又如何呢?观察:思考: 教室的天花板与地面给人平行的感觉,前后两块黑板也是平行的。探究:当三角板的两条边所在直线分别与地面平行时,这个三角板所在平面与地面平行。结论:(1)平面?内有一条直线与平面?平行,?,?平行吗?结论: (1)中的平面α,β不一定平行。如图,借助长方体模型,平面ABCD中直线AD平行平面BCC'B',但平面ABCD与平面BCC'B'不平行。 (2)平面?内有两条直线与平面?
平行,?,?平行吗?探究:结论:(2)分两种情况讨论: 如果平面β内的两条直线是平行直线,
平面α与平面β不一定平行。如图,AD∥PQ,AD∥平面BCC’B’,PQ∥BCC’B’,但平面ABCD与
平面BCC’B’不平行。 如果平面β内的两条直线是相交的直线,两个平面会不会一定平行?直线的条数不是关键直线相交才是关键 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行 两个平面平行的判定定理:线不在多,重在相交符号表示: a??,b??,
a?b=P,
a???,b???图形表示:结论:?????线面平行 面面平行线线平行两个平面平行的判定定理的证明已知:在平面内 ,有两条直线 、 相交且和平面 平行. 求证: . 证明:用反证法证明. 假设 . 同理这与题设 和 是相交直线是矛盾的.推论1:如果一个平面内有两条相交直线分别平行与另一个平面内的两条直线,那么这两个平面平行。推论2:平行于同一个平面的两个平面平行。基础尝试性练习判断下列命题是否正确:
( )1、如果一个平面内有两条直线平行于另一个
平面,那么这两个平面平行;
( ) 2、如果一个平面内有两条不平行的直线都平
行于另一个平面,那么这两个平面平行;
( )3、如果一个平面内有无数条直线分别平行于
另一个平面,那么这两个平面平行;
( )4、如果一个平面内任意一条直线都平行于另
一个平面,那么这两个平面平行. 例1:已知正方体ABCD-A1B1C1D1,求证:平面AB1D1//平面C1BD证明:因为ABCD-A1B1C1D1为正方体,
所以 D1C1∥A1B1,D1C1=A1B1
又AB∥A1B1,AB=A1B1,
∴D1C1∥AB,D1C1=AB,
∴D1C1BA是平行四边形,
∴D1A∥C1B,又D1A 平面C1BD,
CB 平面C1BD.由直线与平面平行的判定,可知同理??D1B1∥平面C1BD,又 D1A∩D1B1=D1,所以,平面AB1D1∥平面C1BD。D1A∥平面C1BD,
2.寻找平行直线可以通过三角形的中位线、梯形的中位线、平行线的判定等来完成。反思~领悟:1. 线线平行 线面平行 面面平行来处理。 变式:在正方体ABCD-A1B1C1D1中,
若 M、N、E、F分别是棱A1B1,A1D1,B1C1,
C1D1的中点,求证:平面AMN//平面EFDB。ABCA1B1C1D1DMNEF∴MN∥B1D1 B1D1∥EF∴MN∥EFMN∥平面BDFEMF∥A1D1, A1D1∥AD∴MF∥AD且MF=A1D1= ADAM ∥DF∴ AM∥平面DBEF∴平面AMN∥平面EFDB 如图:三棱锥P-ABC, D,E,F分别是棱PA,PB,PC中点,
求证:平面DEF∥平面ABC。PDEFABC补充例题NMFEDCBAH1 如图所示,平面ABCD∩平面EFCD = CD,
M、N、H 分别是 DC、CF、CB 的中点,
求证 平面 MNH // 平面 DBF课堂练习 2、已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD的中点PQR求证:PQ∥平面BCE。思路1:在平面BCE内找PQ平行线。思路2:过PQ构造与平面BCE平行的平面。课堂总结:1、面面平行的定义;2、面面平行的判定定理;3、面面平行判定定理的应用:要证面面平行,只要证线面平行,而要证线面平行,只要证线线平行。在立体几何中,往往通过线线、线面、面面间的位置关系的转化使问题得到解决。作业布置:
第62页习题2.2?A组第7,8题。
