鲁教版(五四制)数学六年级下册6.2 幂的乘方与积的乘方 课件(共26张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学六年级下册6.2 幂的乘方与积的乘方 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 09:30:55 | ||
图片预览







文档简介
(共26张PPT)
2022年春鲁教版数学
六年级下册数学精品课件
6.2 幂的乘方与积的乘方
1.经历探索幂的乘方与积的乘方的运算性质的过程,进一步体会幂的意义,提高推理能力和有条理的表达能力.
2.了解幂的乘方与积的乘方的运算性质,并能解决一些问题.
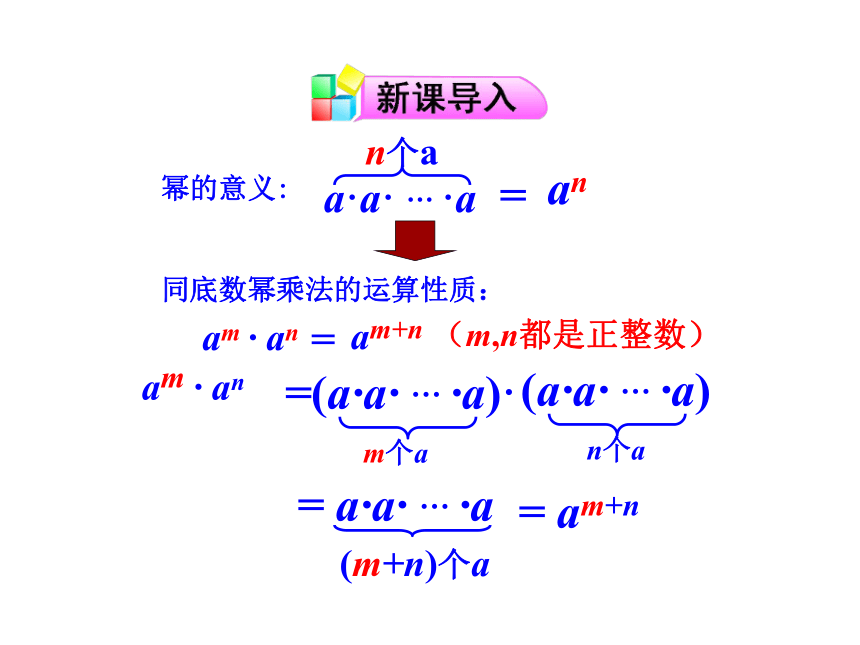
am · an
(a·a· … ·a)
n个a
=(a·a· … ·a)·
m个a
= a·a· … ·a
(m+n)个a
= am+n
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂乘法的运算性质:
am · an
=
am+n
(m,n都是正整数)
乙正方体的棱长是 2 cm, 则乙正方体的体积
V乙= cm3 ;
V甲是V乙 的 倍.
8
125
即53 倍
棱长比的
立方
甲正方体的棱长是乙正方体的 5 倍,则甲正方体的体积
V甲= cm3;
1 000
正方体的体积之比=
正方体的体积比与棱长比的关系:
乙球的半径为 3 cm, 则
乙球的体积V乙= cm3.
V甲 是 V乙 的 倍
即103 倍
球的体积比与半径比的关系
甲球的半径是乙球的10倍,则
甲球的体积V甲= cm3 .
1 000
36
36 000
半径比的
立方
如果甲球的半径是乙球的n倍,那么甲球体积是乙球
体积的 倍.
n3
球的体积之比=
地球、木星、太阳可以近似地看做是球体.木星、太阳的
半径分别约是地球的10倍和102倍,它们的体积分别约是地
球的 倍和 倍.
木星
地球
太阳
体积扩大的倍数比半径扩大的倍数大得多.
103
106
(102)3=106,为什么?
(102)3
=102×102×102
=102+2+2
=102×3
=106
(根据 _____________________)
(根据____________)
同底数幂的乘法性质
幂的意义
(102)3=106,为什么?
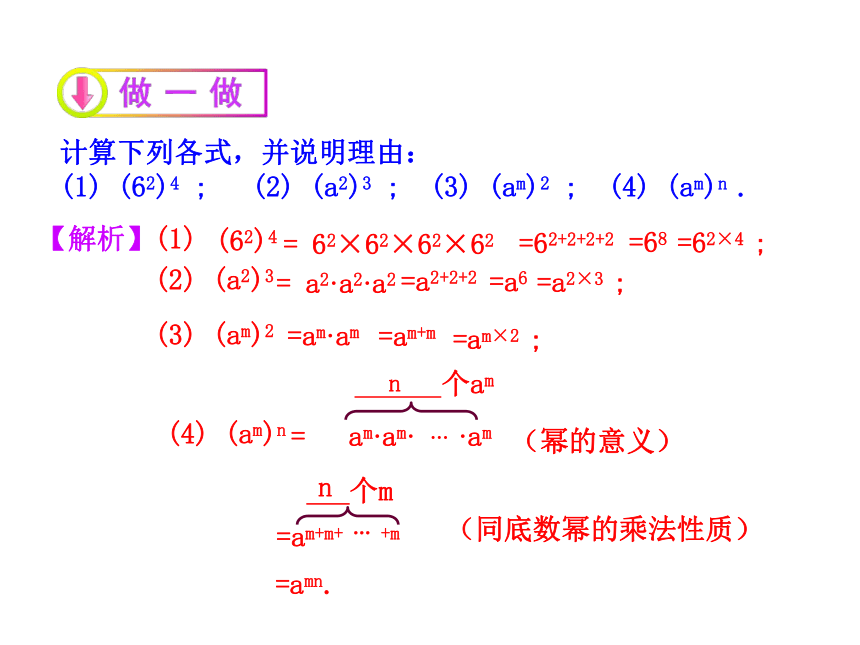
计算下列各式,并说明理由:
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ; (4) (am)n .
【解析】(1)
(2) (a2)3
(3) (am)2
= 62×62×62×62
=62+2+2+2
=68
= a2·a2·a2
=a2+2+2
=a6
=am·am
=am+m
(4) (am)n
= am·am· … ·am
个am
=am+m+ … +m
=amn.
(幂的意义)
(同底数幂的乘法性质)
=62×4 ;
(62)4
n
个m
n
=a2×3 ;
=am×2 ;
(am)n=amn (m,n都是正整数)
底数_______,
幂的乘方,
幂 的 乘 方 法 则
不变
相乘
指数________.
【例1】计算:
(1)(102)3 ; (2)(b5)5; (3)(an)3;
(4)-(x2)m ; (5)(y2)3 · y; (6)2(a2)6-(a3)4.
(6) 2(a2)6-(a3)4
=102×3
=106 ;
(1)(102)3
【解析】
(2) (b5)5
= b5×5
= b25 ;
(3) (an)3
= an×3
=a3n ;
(4) -(x2)m
= -x2×m
= -x2m ;
(5) (y2)3 · y
= y2×3 · y
= y6 · y
=2a2×6-a3×4
=2a12-a12
=a12.
= y7;
1.计算:
(1) (103)3 ; (2)-(a2)5 ; (3)(x3)4·x2 ;
(4) [(-x)2]3 ; (5)(-a)2(a2)2; (6)x·x4–x2·x3 .
2.下面的计算是否正确?如有错误请改正:
(1)(x3)3 = x6 ; (2)a6·a4 =a24 .
答案:(1)109 (2)-a10 (3)x14 (4)x6 (5)a6 (6)0
答案:(1)错,(x3)3 = x9; (2)错,a6 · a4 = a10.
在下面的推导中,说明每一步(变形)的依据:
(ab)n = (ab)·(ab) ·…·(ab) ( )
=(a·a·…·a)· (b·b·…·b) ( )
=an·bn. ( )
幂的意义
乘法交换律、结合律
幂的意义
n个ab
n个a
n个b
(ab)n =
an·bn
上式显示:
积的乘方= .
(ab)n =
an·bn
积的乘方
乘方的积
(n是正整数)
每个因式分别乘方后的积
积的乘方法则
(a+b)n,可以用积的乘方法则计算吗
即“(a+b)n= an·bn ”成立吗?
“(a+b)n= an+bn ”成立吗?
不能
不成立
不成立
【例2】计算:
(1)(3x)2 ; (2)(-2b)5 ;
(3)(-2xy)4 ; (4)(3a2)n .
=32x2
=9x2;
(1)(3x)2
【解析】
(2)(-2b)5
= (-2)5b5
=-32b5;
(3)(-2xy)4
= (-2x)4 y4
=(-2)4 x4 y4
(4)(3a2)n
= 3n (a2)n
=3n a2n.
=16x4 y4;
【例3】地球可以近似地看做是球体,如果用V, r分别
代表球的体积和半径,那么 . 地球的半径约为
6×103 千米,它的体积大约是多少立方千米?
【解析】
=
×(6×103)3
=
×
63×109
≈
9.05×1011
(立方千米)
注意
运算顺序 !
三个或三个以上的积的乘方,是否也具有上面的性质 怎样用公式表示
(abc)n=an·bn·cn
证明:
(abc)n=[(ab)·c]n
=(ab)n·cn
= an·bn·cn.
计算:
(1)(- 3n)3;
(2)(5xy)3;
(3)–a3 +(–4a)2 a.
答案:(1)-27n3
(2)125x3y3
(3)15a3
试用简便方法计算:
(ab)n = an·bn
(n是正整数)
逆用公式:
an·bn = (ab)n
(1) 23×53
(2) 28×58
(3) (-5)16×(-2)15
(4) 24 ×44 ×(-0.125)4
= (2×5)3
= 103.
= (2×5)8
= 108 .
= (-5)×[(-5)×(-2)]15
= -5×1015.
= [2×4×(-0.125)]4
=(-1)4
=1.
1.(济宁·中考)下列等式成立的是( )
(A)a +a =a5 (B)a3-a2=a
(C)a2·a3=a6 (D)(a2)3=a6
【解析】选D.A、B选项不是同类项不能合并,C选项为a5,D选项是正确的.
2.(重庆·中考)(a3)2计算的结果是( )
(A)a (B)a5 (C)a6 (D)a9
【解析】选C.本题考查幂的乘方,即底数不变,指数相乘.即(a3)2=a3×2=a6.
3. 计算 -(-3a)2的结果是( )
(A)-6a2 (B)-9a2 (C)6a2 (D)9a2
【解析】选B.因为-(-3a)2=-[(-3)2·a2]=-9a2.
同底数幂的乘法运算法则:
am·an
am+n
=
同底数幂的乘方运算法则:
(am) n=amn
反向使用am · an =am+n, (am)n =amn (m,n都是正整数)可使某些计算简捷.
积的乘方运算法则: (ab)n=anbn
积的乘方=
每个因式分别乘方后的积
(m,n都是正整数)
(n是正整数)
(m,n都是正整数)
人若志趣不远,心不在焉,虽学不成.
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
六年级下册数学精品课件
6.2 幂的乘方与积的乘方
1.经历探索幂的乘方与积的乘方的运算性质的过程,进一步体会幂的意义,提高推理能力和有条理的表达能力.
2.了解幂的乘方与积的乘方的运算性质,并能解决一些问题.
am · an
(a·a· … ·a)
n个a
=(a·a· … ·a)·
m个a
= a·a· … ·a
(m+n)个a
= am+n
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂乘法的运算性质:
am · an
=
am+n
(m,n都是正整数)
乙正方体的棱长是 2 cm, 则乙正方体的体积
V乙= cm3 ;
V甲是V乙 的 倍.
8
125
即53 倍
棱长比的
立方
甲正方体的棱长是乙正方体的 5 倍,则甲正方体的体积
V甲= cm3;
1 000
正方体的体积之比=
正方体的体积比与棱长比的关系:
乙球的半径为 3 cm, 则
乙球的体积V乙= cm3.
V甲 是 V乙 的 倍
即103 倍
球的体积比与半径比的关系
甲球的半径是乙球的10倍,则
甲球的体积V甲= cm3 .
1 000
36
36 000
半径比的
立方
如果甲球的半径是乙球的n倍,那么甲球体积是乙球
体积的 倍.
n3
球的体积之比=
地球、木星、太阳可以近似地看做是球体.木星、太阳的
半径分别约是地球的10倍和102倍,它们的体积分别约是地
球的 倍和 倍.
木星
地球
太阳
体积扩大的倍数比半径扩大的倍数大得多.
103
106
(102)3=106,为什么?
(102)3
=102×102×102
=102+2+2
=102×3
=106
(根据 _____________________)
(根据____________)
同底数幂的乘法性质
幂的意义
(102)3=106,为什么?
计算下列各式,并说明理由:
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ; (4) (am)n .
【解析】(1)
(2) (a2)3
(3) (am)2
= 62×62×62×62
=62+2+2+2
=68
= a2·a2·a2
=a2+2+2
=a6
=am·am
=am+m
(4) (am)n
= am·am· … ·am
个am
=am+m+ … +m
=amn.
(幂的意义)
(同底数幂的乘法性质)
=62×4 ;
(62)4
n
个m
n
=a2×3 ;
=am×2 ;
(am)n=amn (m,n都是正整数)
底数_______,
幂的乘方,
幂 的 乘 方 法 则
不变
相乘
指数________.
【例1】计算:
(1)(102)3 ; (2)(b5)5; (3)(an)3;
(4)-(x2)m ; (5)(y2)3 · y; (6)2(a2)6-(a3)4.
(6) 2(a2)6-(a3)4
=102×3
=106 ;
(1)(102)3
【解析】
(2) (b5)5
= b5×5
= b25 ;
(3) (an)3
= an×3
=a3n ;
(4) -(x2)m
= -x2×m
= -x2m ;
(5) (y2)3 · y
= y2×3 · y
= y6 · y
=2a2×6-a3×4
=2a12-a12
=a12.
= y7;
1.计算:
(1) (103)3 ; (2)-(a2)5 ; (3)(x3)4·x2 ;
(4) [(-x)2]3 ; (5)(-a)2(a2)2; (6)x·x4–x2·x3 .
2.下面的计算是否正确?如有错误请改正:
(1)(x3)3 = x6 ; (2)a6·a4 =a24 .
答案:(1)109 (2)-a10 (3)x14 (4)x6 (5)a6 (6)0
答案:(1)错,(x3)3 = x9; (2)错,a6 · a4 = a10.
在下面的推导中,说明每一步(变形)的依据:
(ab)n = (ab)·(ab) ·…·(ab) ( )
=(a·a·…·a)· (b·b·…·b) ( )
=an·bn. ( )
幂的意义
乘法交换律、结合律
幂的意义
n个ab
n个a
n个b
(ab)n =
an·bn
上式显示:
积的乘方= .
(ab)n =
an·bn
积的乘方
乘方的积
(n是正整数)
每个因式分别乘方后的积
积的乘方法则
(a+b)n,可以用积的乘方法则计算吗
即“(a+b)n= an·bn ”成立吗?
“(a+b)n= an+bn ”成立吗?
不能
不成立
不成立
【例2】计算:
(1)(3x)2 ; (2)(-2b)5 ;
(3)(-2xy)4 ; (4)(3a2)n .
=32x2
=9x2;
(1)(3x)2
【解析】
(2)(-2b)5
= (-2)5b5
=-32b5;
(3)(-2xy)4
= (-2x)4 y4
=(-2)4 x4 y4
(4)(3a2)n
= 3n (a2)n
=3n a2n.
=16x4 y4;
【例3】地球可以近似地看做是球体,如果用V, r分别
代表球的体积和半径,那么 . 地球的半径约为
6×103 千米,它的体积大约是多少立方千米?
【解析】
=
×(6×103)3
=
×
63×109
≈
9.05×1011
(立方千米)
注意
运算顺序 !
三个或三个以上的积的乘方,是否也具有上面的性质 怎样用公式表示
(abc)n=an·bn·cn
证明:
(abc)n=[(ab)·c]n
=(ab)n·cn
= an·bn·cn.
计算:
(1)(- 3n)3;
(2)(5xy)3;
(3)–a3 +(–4a)2 a.
答案:(1)-27n3
(2)125x3y3
(3)15a3
试用简便方法计算:
(ab)n = an·bn
(n是正整数)
逆用公式:
an·bn = (ab)n
(1) 23×53
(2) 28×58
(3) (-5)16×(-2)15
(4) 24 ×44 ×(-0.125)4
= (2×5)3
= 103.
= (2×5)8
= 108 .
= (-5)×[(-5)×(-2)]15
= -5×1015.
= [2×4×(-0.125)]4
=(-1)4
=1.
1.(济宁·中考)下列等式成立的是( )
(A)a +a =a5 (B)a3-a2=a
(C)a2·a3=a6 (D)(a2)3=a6
【解析】选D.A、B选项不是同类项不能合并,C选项为a5,D选项是正确的.
2.(重庆·中考)(a3)2计算的结果是( )
(A)a (B)a5 (C)a6 (D)a9
【解析】选C.本题考查幂的乘方,即底数不变,指数相乘.即(a3)2=a3×2=a6.
3. 计算 -(-3a)2的结果是( )
(A)-6a2 (B)-9a2 (C)6a2 (D)9a2
【解析】选B.因为-(-3a)2=-[(-3)2·a2]=-9a2.
同底数幂的乘法运算法则:
am·an
am+n
=
同底数幂的乘方运算法则:
(am) n=amn
反向使用am · an =am+n, (am)n =amn (m,n都是正整数)可使某些计算简捷.
积的乘方运算法则: (ab)n=anbn
积的乘方=
每个因式分别乘方后的积
(m,n都是正整数)
(n是正整数)
(m,n都是正整数)
人若志趣不远,心不在焉,虽学不成.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
