鲁教版(五四制)数学六年级下册6.7 完全平方公式 课件(共26张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学六年级下册6.7 完全平方公式 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
2022年春鲁教版数学
六年级下册数学精品课件
6.7 完全平方公式
1.经历探索完全平方公式的过程,进一步增强符号感和推理能力.
2.会推导完全平方公式,并能运用公式进行简单的计算.
3.了解完全平方公式的几何背景.
公式的结构特征:
a2 b2;
左边是两个二项式的乘积,
(a+b)(a b)=
即两数和与这两数差的积.
右边是
两数的平方差.
2.计算:
(3)(a+b)(a+b)
(4)(a-b)(a-b)
(1) (a+b)(a-b)
(2) (-a+b)(-a-b)
1.平方差公式
a
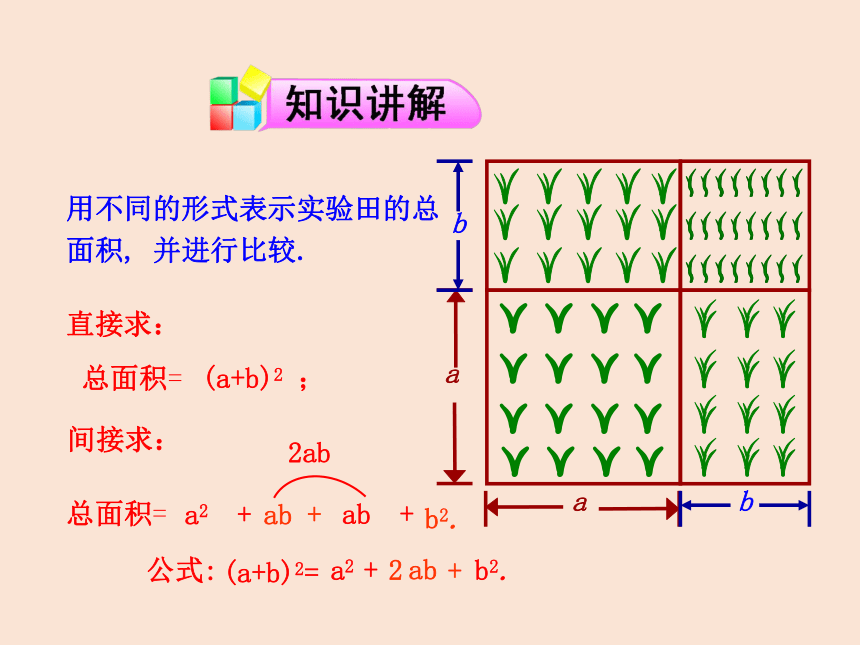
用不同的形式表示实验田的总面积, 并进行比较.
a
b
b
(a+b)2 ;
a2 +
ab +
ab +
b2.
(a+b)2=
a2 +
ab
+
b2.
2
公式:
总面积=
总面积=
直接求:
间接求:
2ab
完全平方公式
(1)你能用多项式的乘法法则来说明它成立吗
(a+b)2=a2+2ab+b2 ;
(2)
a2 2ab+b2.
小颖写出了如下的算式:
(a b)2=
[a+( b)]2
(a b)2=
她是怎么想的
你能继续做下去吗
【解析】(1)(a+b)2 =
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab +
b2.
利用两数和的
完全平方公式
推证公式
(a b)2 =
[a+( b)]2
= + 2 +_____
a2
a
( b)
( b)2
=
a2
2ab
b2.
+
(2)(a-b)2=(a-b)(a-b)=a2-2ab+b2
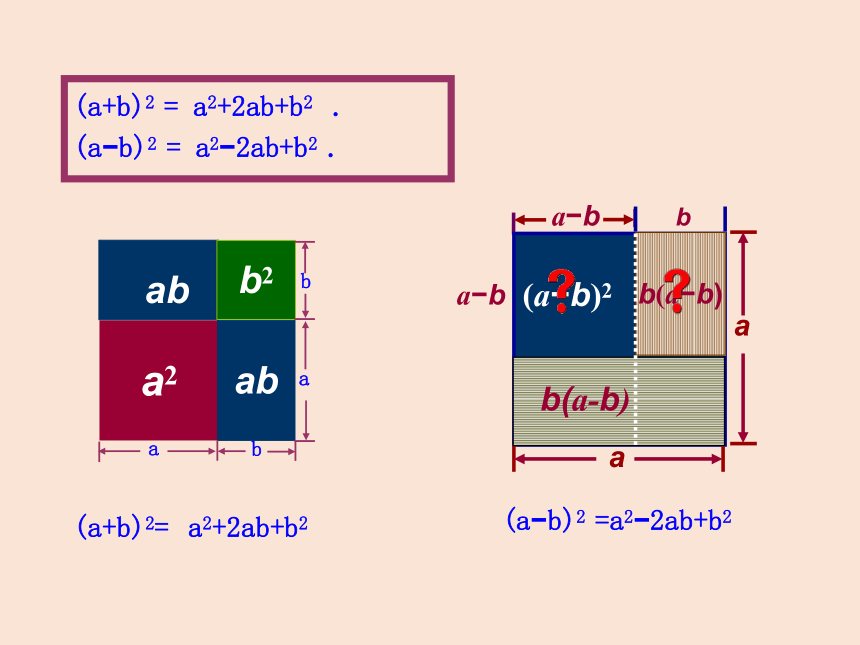
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
a2
ab
ab
b2
(a+b)2=
a b
a b
a
a
b(a-b)
b(a b)
b
(a b)2
a2+2ab+b2
(a b)2 =a2 2ab+b2
a
b
a
b
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
语言表述:
两数和 的平方
等于这两数的平方和
加上 这两数乘积的2倍.
(差)
(减去)
用自己的语言叙述上面的公式
【例1】利用完全平方公式计算:
(2x 3)2
完全平方公式的使用与平方差公式的使用一样,
先把要计算的式子与完全平方公式对照,
明确哪个是a , 哪个是b.
第一个数
4x2
2x
的平方,
( )2
减去
第一个数
与第二个数
2x
3
乘积
的2倍,
2
加上
+
第二个数
3
的平方.
2
=
12x
+
9 ;
【解析】 (2x 3)2
做题时要边念边写:
=
注意:
(1) ( x 2y)2 ;
(2) (2xy+ x )2 ;
计算:
(3)(n +1)2 n2.
1.指出下列各式中的错误,并加以改正:
(1) (2a 1)2=2a2 2a+1;
(2) (2a+1)2=4a2 +1;
(3) ( a 1)2= a2 2a 1.
【解析】
(1)第一数平方时,未添括号;
第一数与第二数乘积的2倍少乘了一个2 ;
应改为:(2a 1)2= (2a)2 2 2a 1+1;
(2)少了第一数与第二数乘积的2倍(丢了一项);
应改为:(2a+1)2=(2a)2+2 2a 1 +1;
(3)第一数平方未添括号,
第一数与第二数乘积的2倍错了符号;
第二数的平方这一项错了符号;
应改为:( a 1)2=( a)2 2 ( a ) 1+( 1)2.
2.下列等式是否成立 不成立的说明理由.
(1) ( 4a+1)2=(1 4a)2;
(2) ( 4a 1)2=(4a+1)2;
(3) (4a 1)(1 4a)=(4a 1)(4a 1)=(4a 1)2;
(4) (4a 1)( 1 4a)=(4a 1)(4a+1).
成立
理由:
成立
(3) 因为 (1 4a)= ( 1+4a)
不成立.
= (4a 1),
所以 (4a 1)(1 4a)=(4a 1)·[ (4a 1)]
= (4a 1)(4a 1)= (4a 1)2.
不成立.
(4) 右边应为:
(4a 1)(4a+1).
(1) 第一天有 a 个孩子一起去了老人家,老人一共给了这些孩子多少块糖果?
a2
(2) 第二天有 b个孩子一起去了老人家,老人一共给了这些孩子多少块糖果?
b2
(3) 第三天这(a+b)个孩子一起去了老人家,老人一共给了这些孩子多少块糖果?
(a+b)2
(4) 这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多?
第三天多;
多多少?
为什么?
多2ab.
因为(a+b)2=a2 + 2ab + b2
(a+b)2 ( a2 + b2 )=a2 + 2ab + b2 a2 b2=2ab.
一位老人非常喜欢孩子,每当有孩子到他家做客时,老人都要拿出糖果招待他们.如果来1个孩子,老人就给这个孩子1块糖果,如果来2个孩子,老人就给每个孩子2块糖果.如果来3个孩子,老人就给每个孩子3块糖果……
【例2】利用完全平方公式计算:(1)1022 ; (2)1972.
完全平方公式(a±b)2=a2 ± 2ab+ b2的左边的底数是两数的和或差.
把 1022 改写成 (a+b)2 还是(a b)2
a,b怎样确定?
【解析】
(1)1022
=(100+2)2
=1002+2×100×2+22
=10 000+400+4
=10 404.
(2)1972
=(200-3)2
=2002-2×200×3+32
=40 000-1 200+9
=38 809.
【例3】计算:(a+b+3)(a+b 3);
若不用一般的多项式乘以多项式法则, 怎样用公式来计算
因为两个多项式不同, 即不能写成( )2的形式,
故不能用完全平方公式来计算,只能用平方差公式来计算.
三项能看成两项吗
平方差公式中的
相等的项(a):
符号相反的项(b):
在本题中分别是什么?
[ (a+b) +3 ][ (a+b) 3 ]
【解析】
(a+b+3) (a+b 3)
=
+3
3
(a+b)
(a+b)
=( )2 2
a+b
3
=a2 +2ab+b2
9.
(a+b)
3
1.(益阳·中考)下列计算正确的是( )
(A)
(B)
(C)
(D)
【解析】选D.选项A的正确结果应为
选项B的正确结果应为
选项C的正确结果应为
故A,B,C都是错误的.
=
,故选项D正确.
2.用完全平方公式计算: 1012; 982.
3.⑴ x2 (x 3)2 ;
⑵ (a+b+3)(a b+3).
答案:2.10 201 9 604
3.(1) 6x-9
(2) a2+6a-b2+9
(1) 962 ;
(2) (a b 3)(a b+3).
4.利用公式计算:
答案:(1)9 216 (2)a2-2ab+b2-9
注意完全平方公式和平方差公式的不同:
(1)形式不同.
(2)结果不同:
完全平方公式的结果是三项,
即 (a b)2=a2 2ab+b2;
平方差公式的结果是两项,
即 (a+b)(a b)=a2 b2.
2.在解题过程中要准确确定a和b,对照公式原形的两边, 做到不丢项、不弄错符号、2ab项不少乘2是运用完全平方公式进行多项式乘法的关键.
1.
3.有时需要进行变形,使变形后的式子符合应用完全平方公式的条件,即为“两数和(或差)的平方”,然后应用公式计算.
理想是指路明灯.没有理想,就没有坚定的方向,而没有方向, 就没有生活.
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
六年级下册数学精品课件
6.7 完全平方公式
1.经历探索完全平方公式的过程,进一步增强符号感和推理能力.
2.会推导完全平方公式,并能运用公式进行简单的计算.
3.了解完全平方公式的几何背景.
公式的结构特征:
a2 b2;
左边是两个二项式的乘积,
(a+b)(a b)=
即两数和与这两数差的积.
右边是
两数的平方差.
2.计算:
(3)(a+b)(a+b)
(4)(a-b)(a-b)
(1) (a+b)(a-b)
(2) (-a+b)(-a-b)
1.平方差公式
a
用不同的形式表示实验田的总面积, 并进行比较.
a
b
b
(a+b)2 ;
a2 +
ab +
ab +
b2.
(a+b)2=
a2 +
ab
+
b2.
2
公式:
总面积=
总面积=
直接求:
间接求:
2ab
完全平方公式
(1)你能用多项式的乘法法则来说明它成立吗
(a+b)2=a2+2ab+b2 ;
(2)
a2 2ab+b2.
小颖写出了如下的算式:
(a b)2=
[a+( b)]2
(a b)2=
她是怎么想的
你能继续做下去吗
【解析】(1)(a+b)2 =
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab +
b2.
利用两数和的
完全平方公式
推证公式
(a b)2 =
[a+( b)]2
= + 2 +_____
a2
a
( b)
( b)2
=
a2
2ab
b2.
+
(2)(a-b)2=(a-b)(a-b)=a2-2ab+b2
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
a2
ab
ab
b2
(a+b)2=
a b
a b
a
a
b(a-b)
b(a b)
b
(a b)2
a2+2ab+b2
(a b)2 =a2 2ab+b2
a
b
a
b
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
语言表述:
两数和 的平方
等于这两数的平方和
加上 这两数乘积的2倍.
(差)
(减去)
用自己的语言叙述上面的公式
【例1】利用完全平方公式计算:
(2x 3)2
完全平方公式的使用与平方差公式的使用一样,
先把要计算的式子与完全平方公式对照,
明确哪个是a , 哪个是b.
第一个数
4x2
2x
的平方,
( )2
减去
第一个数
与第二个数
2x
3
乘积
的2倍,
2
加上
+
第二个数
3
的平方.
2
=
12x
+
9 ;
【解析】 (2x 3)2
做题时要边念边写:
=
注意:
(1) ( x 2y)2 ;
(2) (2xy+ x )2 ;
计算:
(3)(n +1)2 n2.
1.指出下列各式中的错误,并加以改正:
(1) (2a 1)2=2a2 2a+1;
(2) (2a+1)2=4a2 +1;
(3) ( a 1)2= a2 2a 1.
【解析】
(1)第一数平方时,未添括号;
第一数与第二数乘积的2倍少乘了一个2 ;
应改为:(2a 1)2= (2a)2 2 2a 1+1;
(2)少了第一数与第二数乘积的2倍(丢了一项);
应改为:(2a+1)2=(2a)2+2 2a 1 +1;
(3)第一数平方未添括号,
第一数与第二数乘积的2倍错了符号;
第二数的平方这一项错了符号;
应改为:( a 1)2=( a)2 2 ( a ) 1+( 1)2.
2.下列等式是否成立 不成立的说明理由.
(1) ( 4a+1)2=(1 4a)2;
(2) ( 4a 1)2=(4a+1)2;
(3) (4a 1)(1 4a)=(4a 1)(4a 1)=(4a 1)2;
(4) (4a 1)( 1 4a)=(4a 1)(4a+1).
成立
理由:
成立
(3) 因为 (1 4a)= ( 1+4a)
不成立.
= (4a 1),
所以 (4a 1)(1 4a)=(4a 1)·[ (4a 1)]
= (4a 1)(4a 1)= (4a 1)2.
不成立.
(4) 右边应为:
(4a 1)(4a+1).
(1) 第一天有 a 个孩子一起去了老人家,老人一共给了这些孩子多少块糖果?
a2
(2) 第二天有 b个孩子一起去了老人家,老人一共给了这些孩子多少块糖果?
b2
(3) 第三天这(a+b)个孩子一起去了老人家,老人一共给了这些孩子多少块糖果?
(a+b)2
(4) 这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多?
第三天多;
多多少?
为什么?
多2ab.
因为(a+b)2=a2 + 2ab + b2
(a+b)2 ( a2 + b2 )=a2 + 2ab + b2 a2 b2=2ab.
一位老人非常喜欢孩子,每当有孩子到他家做客时,老人都要拿出糖果招待他们.如果来1个孩子,老人就给这个孩子1块糖果,如果来2个孩子,老人就给每个孩子2块糖果.如果来3个孩子,老人就给每个孩子3块糖果……
【例2】利用完全平方公式计算:(1)1022 ; (2)1972.
完全平方公式(a±b)2=a2 ± 2ab+ b2的左边的底数是两数的和或差.
把 1022 改写成 (a+b)2 还是(a b)2
a,b怎样确定?
【解析】
(1)1022
=(100+2)2
=1002+2×100×2+22
=10 000+400+4
=10 404.
(2)1972
=(200-3)2
=2002-2×200×3+32
=40 000-1 200+9
=38 809.
【例3】计算:(a+b+3)(a+b 3);
若不用一般的多项式乘以多项式法则, 怎样用公式来计算
因为两个多项式不同, 即不能写成( )2的形式,
故不能用完全平方公式来计算,只能用平方差公式来计算.
三项能看成两项吗
平方差公式中的
相等的项(a):
符号相反的项(b):
在本题中分别是什么?
[ (a+b) +3 ][ (a+b) 3 ]
【解析】
(a+b+3) (a+b 3)
=
+3
3
(a+b)
(a+b)
=( )2 2
a+b
3
=a2 +2ab+b2
9.
(a+b)
3
1.(益阳·中考)下列计算正确的是( )
(A)
(B)
(C)
(D)
【解析】选D.选项A的正确结果应为
选项B的正确结果应为
选项C的正确结果应为
故A,B,C都是错误的.
=
,故选项D正确.
2.用完全平方公式计算: 1012; 982.
3.⑴ x2 (x 3)2 ;
⑵ (a+b+3)(a b+3).
答案:2.10 201 9 604
3.(1) 6x-9
(2) a2+6a-b2+9
(1) 962 ;
(2) (a b 3)(a b+3).
4.利用公式计算:
答案:(1)9 216 (2)a2-2ab+b2-9
注意完全平方公式和平方差公式的不同:
(1)形式不同.
(2)结果不同:
完全平方公式的结果是三项,
即 (a b)2=a2 2ab+b2;
平方差公式的结果是两项,
即 (a+b)(a b)=a2 b2.
2.在解题过程中要准确确定a和b,对照公式原形的两边, 做到不丢项、不弄错符号、2ab项不少乘2是运用完全平方公式进行多项式乘法的关键.
1.
3.有时需要进行变形,使变形后的式子符合应用完全平方公式的条件,即为“两数和(或差)的平方”,然后应用公式计算.
理想是指路明灯.没有理想,就没有坚定的方向,而没有方向, 就没有生活.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
