2021-2022学年度人教版八年级数学下册 17.2勾股定理 的逆定律 同步练习(word版、含答案)
文档属性
| 名称 | 2021-2022学年度人教版八年级数学下册 17.2勾股定理 的逆定律 同步练习(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 68.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 14:28:50 | ||
图片预览


文档简介
2021-2022学年度人教版八年级数学下册
17.2勾股定理 的逆定律 同步练习(含答案)
一、单选题
1.已知△ABC的三边长分别为5,13,12,则△ABC的面积为( )
A.30 B.60 C.78 D.不能确定
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,, C.6,7,8 D.2,3,4
3.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三条边的比是1∶2∶3 B.三条边满足关系a2=c2-b2
C.三个角的比是1∶2∶3 D.三个角满足关系∠B+∠C=∠A
4.如图,正方形ABCD的面积是( )
A.5 B.25 C.7 D.1
5.如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为5m,梯子的顶端B到地面的距离为12m,现将梯子的底端A向外移动到A',使梯子的底端A'到墙根O的距离等于6m,同时梯子的顶端B下降至B',那么BB'( )
A.小于1m B.大于1m
C.等于1m D.小于或等于1m
6.下列四组数据表示三角形的三边长,其中不能构成直角三角形的一组数据是( )
A.1 cm, cm, 4cm B.5cm, 12cm, 13cm:
C.3cm, 4cm, 5cm: D.7cm, 24cm, 25 cm
7.下列是勾股数的有( )
① 3、4、5;② 5、12 、13;③ 9、40 、41;④ 13、14、15;⑤ ;⑥ 11 、60 、61
A.6组 B.5组 C.4组 D.3组
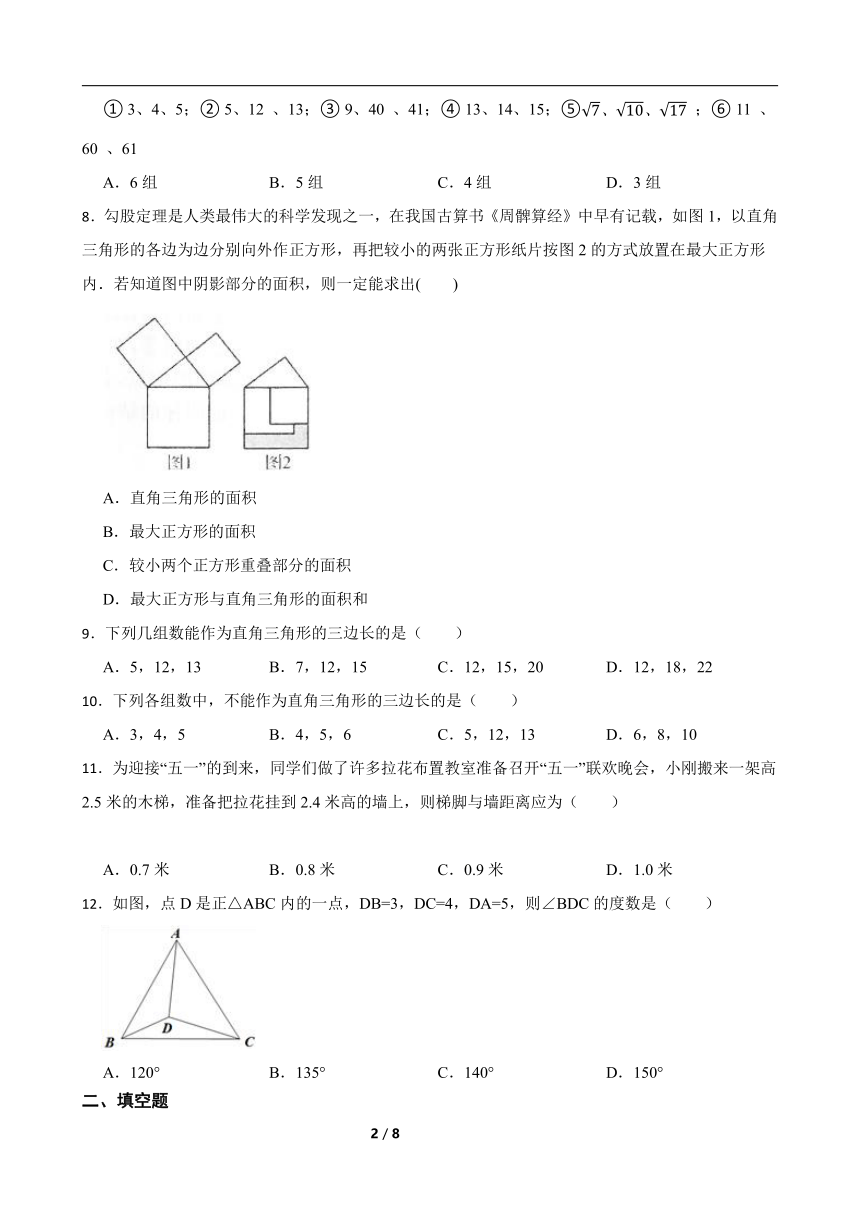
8.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载,如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
9.下列几组数能作为直角三角形的三边长的是( )
A.5,12,13 B.7,12,15 C.12,15,20 D.12,18,22
10.下列各组数中,不能作为直角三角形的三边长的是( )
A.3,4,5 B.4,5,6 C.5,12,13 D.6,8,10
11.为迎接“五一”的到来,同学们做了许多拉花布置教室准备召开“五一”联欢晚会,小刚搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙距离应为( )
A.0.7米 B.0.8米 C.0.9米 D.1.0米
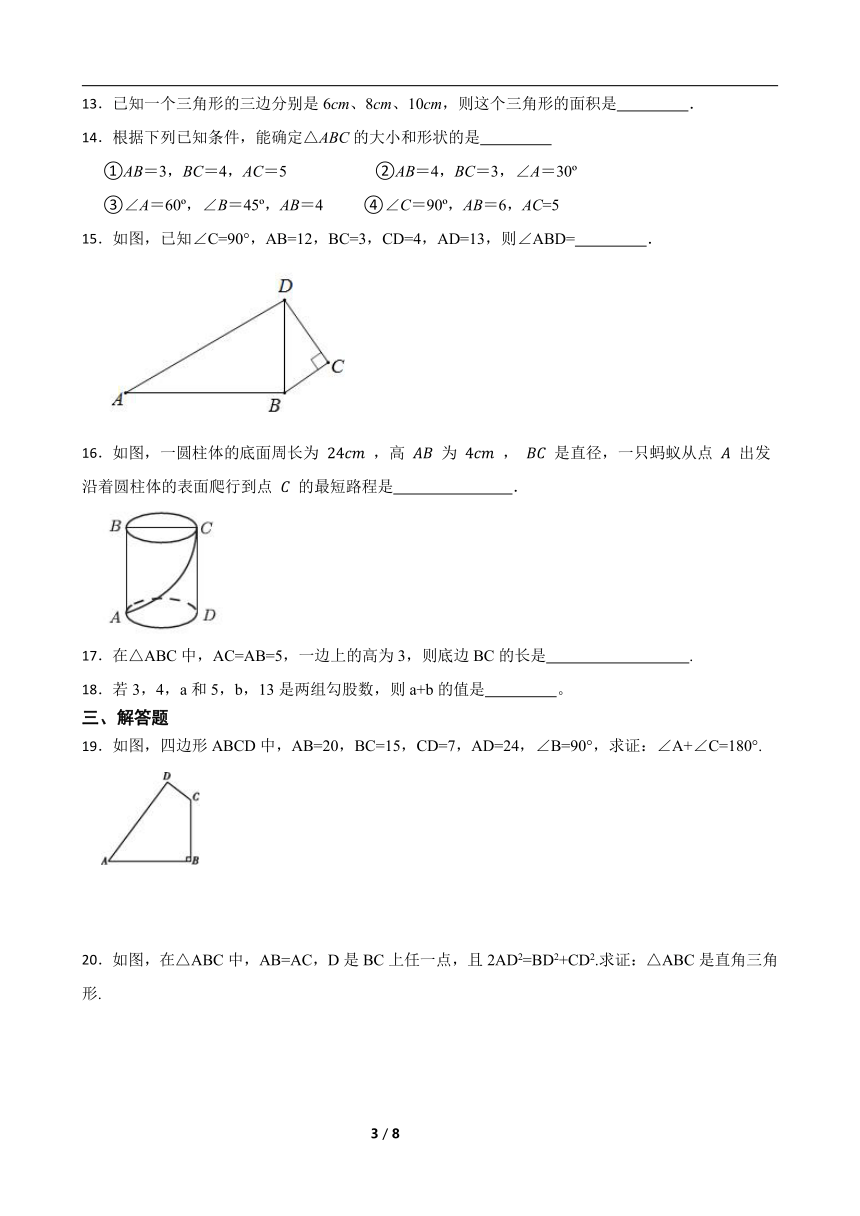
12.如图,点D是正△ABC内的一点,DB=3,DC=4,DA=5,则∠BDC的度数是( )
A.120° B.135° C.140° D.150°
二、填空题
13.已知一个三角形的三边分别是6cm、8cm、10cm,则这个三角形的面积是 .
14.根据下列已知条件,能确定△ABC的大小和形状的是
①AB=3,BC=4,AC=5 ②AB=4,BC=3,∠A=30
③∠A=60 ,∠B=45 ,AB=4 ④∠C=90 ,AB=6,AC=5
15.如图,已知∠C=90°,AB=12,BC=3,CD=4,AD=13,则∠ABD= .
16.如图,一圆柱体的底面周长为 ,高 为 , 是直径,一只蚂蚁从点 出发沿着圆柱体的表面爬行到点 的最短路程是 .
17.在△ABC中,AC=AB=5,一边上的高为3,则底边BC的长是 .
18.若3,4,a和5,b,13是两组勾股数,则a+b的值是 。
三、解答题
19.如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠A+∠C=180°.
20.如图,在△ABC中,AB=AC,D是BC上任一点,且2AD2=BD2+CD2.求证:△ABC是直角三角形.
21.小明想知道学校的旗杆有多高,他发现旗杆顶上的绳子BD垂到地面还多CD=1米,当他把绳子的下端D拉开5米到后,发现下端D刚好接触地面A.你能帮他把旗杆的高度求出来吗?
22.如图,在一棵树的10米高B处有两只猴子,其中一只爬下树走向离树20米的池塘C,而另一只爬到树顶D后直扑池塘C,结果两只猴子经过的距离相等,问这棵树有多高?
23.如图,四边形ABCD中,AB=AD,∠BAD=90°,若AB=2 ,CD=4 ,BC=8,求四边形ABCD的面积.
四、综合题
24.已知a、b、c满足|a- |+ +(c-4 )2=0
(1)求a、b、c的值:
(2)判断以a、b、c为边的三角形的形状,并说明理由。
答案解析部分
1.A
2.B
3.A
4.B
5.A
6.A
7.B
8.C
9.A
10.B
11.A
12.D
13.24cm2
14.①③④
15.90°
16.
17.8或 或
18.17
19.证明:连接AC.
∵AB=20,BC=15,∠B=90°,
∴由勾股定理,得AC2=202+152=625
又CD=7,AD=24,
∴CD2+AD2=625,
∴AC2=CD2+AD2
∴∠D=90°,
∴∠A+∠C=360° 180°=180°
20.证明:作AE⊥BC于E,如图所示:由题意得:ED=BD-BE=CE-CD,在△ABC中,AB=AC,BE=CE。由勾股定理可得:AD2=AE2+DE2BD2+CD2=(BE+ED)2+(CE-DE)2=BE2+CE2+2DE2,2AD2=BD2+CD2.2AE2+2DE2=BE2+CE2+2DE22AE2=BE2+CE2,AE=BE=CE.△AEB与△AEC都是等腰直角三角形,∠BAE=∠CAE=45°,∠BAC=90°,△ABC是直角三角形.
21.解:由题意得:AC=5米,AB=(BC+1)米,
∵BC2+AC2=AB2,
∴BC2+52=(BC+1)2,
解得:BC=12.
答:旗杆的高度是12米.
22.解:设BD=x米,则AD=(10+x)米,CD=(30﹣x)米,
根据题意,得:
(30﹣x)2﹣(x+10)2=202,
解得x=5.
即树的高度是10+5=15米.
23.解:∵ AB=AD,∠BAD=90°,AB= ,
∴ BD= =4,
∵ BD2+CD2=42+( )2=64,BC2=64,
∴ BD2+CD2=BC2,
∴ △BCD为直角三角形,
∴S四边形ABCD=S△ABD+S△BCD= × × + × ×4=4+8
24.(1)解:根据题意得:a- =0,b-5=0,c-4 =0,
解得:a= ,b=5,c=4
(2)解:以a、b、c为边的三角形是直角三角形,理由如下:
∵a2+b2=( )2+52= 32
c2=(4 )2=32,
∴a2+b2=c2,
∴以a、b、c为边的三角形是直角三角形
8 / 8
17.2勾股定理 的逆定律 同步练习(含答案)
一、单选题
1.已知△ABC的三边长分别为5,13,12,则△ABC的面积为( )
A.30 B.60 C.78 D.不能确定
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,, C.6,7,8 D.2,3,4
3.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三条边的比是1∶2∶3 B.三条边满足关系a2=c2-b2
C.三个角的比是1∶2∶3 D.三个角满足关系∠B+∠C=∠A
4.如图,正方形ABCD的面积是( )
A.5 B.25 C.7 D.1
5.如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为5m,梯子的顶端B到地面的距离为12m,现将梯子的底端A向外移动到A',使梯子的底端A'到墙根O的距离等于6m,同时梯子的顶端B下降至B',那么BB'( )
A.小于1m B.大于1m
C.等于1m D.小于或等于1m
6.下列四组数据表示三角形的三边长,其中不能构成直角三角形的一组数据是( )
A.1 cm, cm, 4cm B.5cm, 12cm, 13cm:
C.3cm, 4cm, 5cm: D.7cm, 24cm, 25 cm
7.下列是勾股数的有( )
① 3、4、5;② 5、12 、13;③ 9、40 、41;④ 13、14、15;⑤ ;⑥ 11 、60 、61
A.6组 B.5组 C.4组 D.3组
8.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载,如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
9.下列几组数能作为直角三角形的三边长的是( )
A.5,12,13 B.7,12,15 C.12,15,20 D.12,18,22
10.下列各组数中,不能作为直角三角形的三边长的是( )
A.3,4,5 B.4,5,6 C.5,12,13 D.6,8,10
11.为迎接“五一”的到来,同学们做了许多拉花布置教室准备召开“五一”联欢晚会,小刚搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙距离应为( )
A.0.7米 B.0.8米 C.0.9米 D.1.0米
12.如图,点D是正△ABC内的一点,DB=3,DC=4,DA=5,则∠BDC的度数是( )
A.120° B.135° C.140° D.150°
二、填空题
13.已知一个三角形的三边分别是6cm、8cm、10cm,则这个三角形的面积是 .
14.根据下列已知条件,能确定△ABC的大小和形状的是
①AB=3,BC=4,AC=5 ②AB=4,BC=3,∠A=30
③∠A=60 ,∠B=45 ,AB=4 ④∠C=90 ,AB=6,AC=5
15.如图,已知∠C=90°,AB=12,BC=3,CD=4,AD=13,则∠ABD= .
16.如图,一圆柱体的底面周长为 ,高 为 , 是直径,一只蚂蚁从点 出发沿着圆柱体的表面爬行到点 的最短路程是 .
17.在△ABC中,AC=AB=5,一边上的高为3,则底边BC的长是 .
18.若3,4,a和5,b,13是两组勾股数,则a+b的值是 。
三、解答题
19.如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠A+∠C=180°.
20.如图,在△ABC中,AB=AC,D是BC上任一点,且2AD2=BD2+CD2.求证:△ABC是直角三角形.
21.小明想知道学校的旗杆有多高,他发现旗杆顶上的绳子BD垂到地面还多CD=1米,当他把绳子的下端D拉开5米到后,发现下端D刚好接触地面A.你能帮他把旗杆的高度求出来吗?
22.如图,在一棵树的10米高B处有两只猴子,其中一只爬下树走向离树20米的池塘C,而另一只爬到树顶D后直扑池塘C,结果两只猴子经过的距离相等,问这棵树有多高?
23.如图,四边形ABCD中,AB=AD,∠BAD=90°,若AB=2 ,CD=4 ,BC=8,求四边形ABCD的面积.
四、综合题
24.已知a、b、c满足|a- |+ +(c-4 )2=0
(1)求a、b、c的值:
(2)判断以a、b、c为边的三角形的形状,并说明理由。
答案解析部分
1.A
2.B
3.A
4.B
5.A
6.A
7.B
8.C
9.A
10.B
11.A
12.D
13.24cm2
14.①③④
15.90°
16.
17.8或 或
18.17
19.证明:连接AC.
∵AB=20,BC=15,∠B=90°,
∴由勾股定理,得AC2=202+152=625
又CD=7,AD=24,
∴CD2+AD2=625,
∴AC2=CD2+AD2
∴∠D=90°,
∴∠A+∠C=360° 180°=180°
20.证明:作AE⊥BC于E,如图所示:由题意得:ED=BD-BE=CE-CD,在△ABC中,AB=AC,BE=CE。由勾股定理可得:AD2=AE2+DE2BD2+CD2=(BE+ED)2+(CE-DE)2=BE2+CE2+2DE2,2AD2=BD2+CD2.2AE2+2DE2=BE2+CE2+2DE22AE2=BE2+CE2,AE=BE=CE.△AEB与△AEC都是等腰直角三角形,∠BAE=∠CAE=45°,∠BAC=90°,△ABC是直角三角形.
21.解:由题意得:AC=5米,AB=(BC+1)米,
∵BC2+AC2=AB2,
∴BC2+52=(BC+1)2,
解得:BC=12.
答:旗杆的高度是12米.
22.解:设BD=x米,则AD=(10+x)米,CD=(30﹣x)米,
根据题意,得:
(30﹣x)2﹣(x+10)2=202,
解得x=5.
即树的高度是10+5=15米.
23.解:∵ AB=AD,∠BAD=90°,AB= ,
∴ BD= =4,
∵ BD2+CD2=42+( )2=64,BC2=64,
∴ BD2+CD2=BC2,
∴ △BCD为直角三角形,
∴S四边形ABCD=S△ABD+S△BCD= × × + × ×4=4+8
24.(1)解:根据题意得:a- =0,b-5=0,c-4 =0,
解得:a= ,b=5,c=4
(2)解:以a、b、c为边的三角形是直角三角形,理由如下:
∵a2+b2=( )2+52= 32
c2=(4 )2=32,
∴a2+b2=c2,
∴以a、b、c为边的三角形是直角三角形
8 / 8
