2021-2022学年度初中数学北师大版八年级下册4.3因式分解- 公式法 同步练习(word版、含答案)
文档属性
| 名称 | 2021-2022学年度初中数学北师大版八年级下册4.3因式分解- 公式法 同步练习(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 46.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 14:46:59 | ||
图片预览



文档简介
初中数学北师大版八年级下册第四章第三节 公式法 同步练习
一、单选题
1.下列多项式能用平方差公式分解因式的是( )
A.4x2+y2 B.-4x2-y2 C.-4x2+y2 D.-4x+y2
2.因式分解: ( )
A. B.
C. D.
3.下列式子直接能用完全平方公式进行因式分解的是( )
A. B. C. D.
4.若a,b,c分别是 ABC的三边长,且满足a2﹣2ab+b2=0,b2﹣c2=0,则 ABC的形状是( )
A.直角三角形 B.钝角三角形
C.等腰直角三角形 D.等边三角形
5.a4b-6a3b+9a2b分解因式的正确结果是( )
A.a b(a -6a+9) B.a b(a+3)(a-3)
C.b(a -3) D.a b(a-3)
6.若一个三角形的三边长为a,b,c,且满足a2-2ab+b2+ac-bc =0,则这个三角形是( )
A.直角三角形 B.等边三角形
C.等腰三角形 D.等腰直角三角形
7.如图,长与宽分别为a、b的长方形,它的周长为14,面积为10,则a3b+2a2b2+ab3的值为( )
A.2560 B.490 C.70 D.49
8.如图,在长方形 ABCD 中,E 为 AB 中点,以 BE 为边作正方形 BEFG,边 EF 交 CD 于点H,在边 BE 上取点 M 使BM=BC,作 MN∥BG 交 CD 于点 L,交 FG 于点 N.
欧几里得在《几何原本》中利用该图解释了 ,连结AC,记△ABC的面积为 ,图中阴影部分的面积为 .若 ,则 的值为 ( )
A. B. C. D.
二、填空题
9.分解因式:7a2﹣63=
10.4x2-(k-1)x+1能用完全平方公式因式分解,则k的值为
11.已知x+y=2,则 (x2+2xy+y2)的值为 .
12.下列因式分解正确的是 (填序号)
①;②;③;④
13.由多项式与多项式相乘的法则可知:
即:(a+b)(a2﹣ab+b2)=a3﹣a2b+ab2+a2b﹣ab2+b3=a3+b3
即:(a+b)(a2﹣ab+b2)=a3+b3①,我们把等式①叫做多项式乘法的立方和公式.
同理,(a﹣b)(a2+ab+b2)=a3﹣b3②,我们把等式②叫做多项式乘法的立方差公式.
请利用公式分解因式:﹣64x3+y3= .
14.甲、乙两个同学分解因式x2+ax+b时,甲看错了b,分解结果为(x+2)(x+4);乙看错了a,分解结果为(x+1)(x+9),则多项式x2+ax+b分解因式的正确结果为 .
15.在实数范围内因式分解:x2﹣3= ,3x2﹣5x+2= .
16.观察下列各式:
(x 1)(x+1)=x 1
(x 1)(x +x+1)=x 1
(x 1)(x +x +x+1)=x 1…
根据以上规律, 求1+2+2 +…+ .
三、计算题
17.因式分解
(1)
(2)
18.计算题:
(1)因式分解:(x2+y2)2-4x2y2;
(2)计算:8(1+72)(1+74)(1+78)(1+716).
19.利用因式分解进行计算
(1)
(2)
四、解答题
20.分解因式
(1)
(2)
(3)
(4)(a2+4)2﹣16a2
21.第一环节:自主阅读材料:
常用的分解因式方法有提公因式、公式法等.但有的多项式只用上述方法就无法分解,如x2-4y2+2x-4y,细心观察这个式子会发现前两项符合平方差公式,后两项可提取公因式,分解过程为:
x2-4y2+2x-4y
=(x2-4y2)+(2x-4y) ……分组
=(x-2y)(x+2y)+2(x-2y) ……组内分解因式
=(x-2y)(x+2y+2) ……整体思想提公因式
这种分解因式的方法叫分组分解法。
第二环节:利用这种方法解决下列问题。
因式分解:x2y-4y-2x2+8.
第三环节:拓展运用。
已知a,b,c为△ABC的三边,且b2+2ab=c2+2ac,试判断△ABC的形状.
22.如果n是正整数,求证:3n+2-2n+2+3n-2n能被10整除.
五、综合题
23.先阅读,再解答下列问题.
已知(a2+b2)-8(a2+b2)2+16=0,求a2+b2的值.
错解:设(a2+b2)2=m,
则原式可化为m2-8m+16=0,
即(m-4)2=0,解得m=4.
由(a2+b2)2=4,得a2+b2=±2
(1)上述解答过程错在哪里?为什么?
(2)请你用上述方法分解因式:(a+b)2-14(a+b)+49
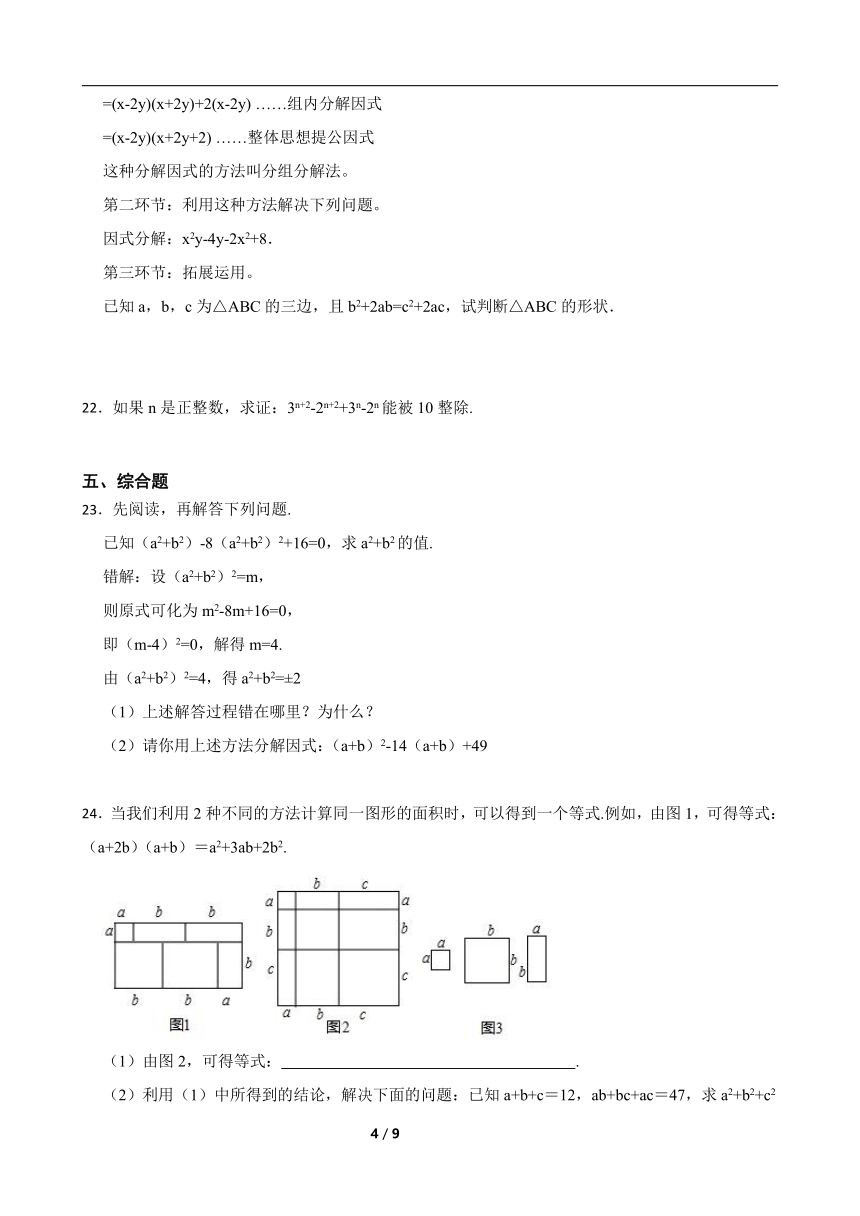
24.当我们利用2种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图2,可得等式: .
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=12,ab+bc+ac=47,求a2+b2+c2的值;
(3)利用图3中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b)
25.(阅读材料)把形如ax2+bx+c的二次三项式(或其一部分)经过适当变形配成完全平方式的方法叫配方法,配方法在因式分解、证明恒等式、利用a2≥0求代数式最值等问题中都有广泛应用.
例如:利用配方法将x2﹣6x+8变形为a(x+m)2+n的形式,并把二次三项式分解因式.
配方:x2﹣6x+8
=x2﹣6x+32﹣32+8
=(x﹣3)2﹣1
分解因式:x2﹣6x+8
=(x﹣3)2﹣1
=(x﹣3+1)(x﹣3﹣1)
=(x﹣2)(x﹣4)
(解决问题)根据以上材料,解答下列问题:
(1)利用配方法将多项式x2﹣4x﹣5化成a(x+m)2+n的形式.
(2)利用配方法把二次三项式x2﹣2x﹣35分解因式.
(3)若a、b、c分别是 ABC的三边,且a2+2b2+3c2﹣2ab﹣2b﹣6c+4=0,试判断 ABC的形状,并说明理由.
(4)求证:无论x,y取任何实数,代数式x2+y2+4x﹣6y+15的值恒为正数.
答案解析部分
1.C
2.C
3.A
4.D
5.D
6.C
7.B
8.C
9.7(a﹣3)(a+3)
10.5或﹣3
11.2
12.①④
13.
14.
15.;(3x-2)(x-1)
16.22018-1
17.(1)解:原式
(2)解:原式
18.(1)解:
=
=
=
=
(2)解:∵ ,
∴原式=
=
=
=
=
= ;
19.(1)解:原式
(2)解:原式
=3+7+11+15+19
=55
20.(1)解:原式
(2)解:原式
(3)解:原式
(4)解:原式 .
21.解:第二环节:x2y﹣4y﹣2x2+8
=(x2y﹣4y)﹣(2x2﹣8)
=y(x2﹣4)﹣2(x2﹣4)
=(y﹣2)(x2﹣4)
=(y﹣2)(x+2)(x﹣2)
b2+2ab=c2+2ac,
第三环节:
b2﹣c2﹣2ab﹣2ac=0,
(b+c)(b﹣c)+2a(b﹣c)=0,
(2a+b+c)(b﹣c)=0,
∵2a+b+c≠0,
∴b﹣c=0,
即b=c,
所以,△ABC是等腰三角形
22.证明:∵3n+2-2n+2+3n-2n
=3n 32-2n 22+3n-2n
=3n(32+1)-2n(22+1)
=10 3n-10 2n-1
=10(3n-2n-1).
∴3n+2-2n+2+3n-2n能被10整除.
23.(1)解:错误:设(a2+b2)2=m,应注意m≥0,且a2+b2≥0,所以由(m-4)2=0,解得m=4由(a2+b2)2=4,得a2+b2=2.
(2)解:设a+b=m,则原式可化为m2-14m+49,即(m-7)2.
∴(a+b)2-14(a+b)+49=(a+b-7)2.
24.(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)解:∵a+b+c=12,ab+bc+ac=47,
∴a2+b2+c2=(a+b+c)2﹣2(ab+ac+bc)=144﹣94=50;
故答案为:50
(3)解:根据题意作图如下:
25.(1)解:x2﹣4x﹣5
=x2﹣4x+22﹣22﹣5
=(x﹣2)2﹣9.
(2)x2﹣2x﹣35
=x2﹣2x+1﹣1﹣35
=(x﹣1)2﹣62
=(x﹣1+6)(x﹣1﹣6)
=(x+5)(x﹣7).
(3)△ABC为等边三角形,理由如下:
∵a2+2b2+3c2﹣2ab﹣2b﹣6c+4=0,
∴(a2﹣2ab+b2)+(b2﹣2b+1)+3(c2﹣2c+1)=0,
∴(a﹣b)2+(b﹣1)2+3(c﹣1)2=0,
∵(a﹣b)2≥0,(b﹣1)2≥0,3(c﹣1)2≥0,
∴a﹣b=0,b﹣1=0,c﹣1=0,
∴a=b,b=1,c=1,
∴a=b=c,
∴△ABC为等边三角形.
(4)证明:x2+y2+4x﹣6y+15
=x2+4x+4+y2﹣6y+9+2
=(x+2)2+(y﹣3)2+2,
∵(x+2)2≥0,(y﹣3)2≥0,
∴(x+2)2+(y﹣3)2+2≥2,
∴代数式x2+y2+4x﹣6y+15的值恒为正数.
9 / 9
一、单选题
1.下列多项式能用平方差公式分解因式的是( )
A.4x2+y2 B.-4x2-y2 C.-4x2+y2 D.-4x+y2
2.因式分解: ( )
A. B.
C. D.
3.下列式子直接能用完全平方公式进行因式分解的是( )
A. B. C. D.
4.若a,b,c分别是 ABC的三边长,且满足a2﹣2ab+b2=0,b2﹣c2=0,则 ABC的形状是( )
A.直角三角形 B.钝角三角形
C.等腰直角三角形 D.等边三角形
5.a4b-6a3b+9a2b分解因式的正确结果是( )
A.a b(a -6a+9) B.a b(a+3)(a-3)
C.b(a -3) D.a b(a-3)
6.若一个三角形的三边长为a,b,c,且满足a2-2ab+b2+ac-bc =0,则这个三角形是( )
A.直角三角形 B.等边三角形
C.等腰三角形 D.等腰直角三角形
7.如图,长与宽分别为a、b的长方形,它的周长为14,面积为10,则a3b+2a2b2+ab3的值为( )
A.2560 B.490 C.70 D.49
8.如图,在长方形 ABCD 中,E 为 AB 中点,以 BE 为边作正方形 BEFG,边 EF 交 CD 于点H,在边 BE 上取点 M 使BM=BC,作 MN∥BG 交 CD 于点 L,交 FG 于点 N.
欧几里得在《几何原本》中利用该图解释了 ,连结AC,记△ABC的面积为 ,图中阴影部分的面积为 .若 ,则 的值为 ( )
A. B. C. D.
二、填空题
9.分解因式:7a2﹣63=
10.4x2-(k-1)x+1能用完全平方公式因式分解,则k的值为
11.已知x+y=2,则 (x2+2xy+y2)的值为 .
12.下列因式分解正确的是 (填序号)
①;②;③;④
13.由多项式与多项式相乘的法则可知:
即:(a+b)(a2﹣ab+b2)=a3﹣a2b+ab2+a2b﹣ab2+b3=a3+b3
即:(a+b)(a2﹣ab+b2)=a3+b3①,我们把等式①叫做多项式乘法的立方和公式.
同理,(a﹣b)(a2+ab+b2)=a3﹣b3②,我们把等式②叫做多项式乘法的立方差公式.
请利用公式分解因式:﹣64x3+y3= .
14.甲、乙两个同学分解因式x2+ax+b时,甲看错了b,分解结果为(x+2)(x+4);乙看错了a,分解结果为(x+1)(x+9),则多项式x2+ax+b分解因式的正确结果为 .
15.在实数范围内因式分解:x2﹣3= ,3x2﹣5x+2= .
16.观察下列各式:
(x 1)(x+1)=x 1
(x 1)(x +x+1)=x 1
(x 1)(x +x +x+1)=x 1…
根据以上规律, 求1+2+2 +…+ .
三、计算题
17.因式分解
(1)
(2)
18.计算题:
(1)因式分解:(x2+y2)2-4x2y2;
(2)计算:8(1+72)(1+74)(1+78)(1+716).
19.利用因式分解进行计算
(1)
(2)
四、解答题
20.分解因式
(1)
(2)
(3)
(4)(a2+4)2﹣16a2
21.第一环节:自主阅读材料:
常用的分解因式方法有提公因式、公式法等.但有的多项式只用上述方法就无法分解,如x2-4y2+2x-4y,细心观察这个式子会发现前两项符合平方差公式,后两项可提取公因式,分解过程为:
x2-4y2+2x-4y
=(x2-4y2)+(2x-4y) ……分组
=(x-2y)(x+2y)+2(x-2y) ……组内分解因式
=(x-2y)(x+2y+2) ……整体思想提公因式
这种分解因式的方法叫分组分解法。
第二环节:利用这种方法解决下列问题。
因式分解:x2y-4y-2x2+8.
第三环节:拓展运用。
已知a,b,c为△ABC的三边,且b2+2ab=c2+2ac,试判断△ABC的形状.
22.如果n是正整数,求证:3n+2-2n+2+3n-2n能被10整除.
五、综合题
23.先阅读,再解答下列问题.
已知(a2+b2)-8(a2+b2)2+16=0,求a2+b2的值.
错解:设(a2+b2)2=m,
则原式可化为m2-8m+16=0,
即(m-4)2=0,解得m=4.
由(a2+b2)2=4,得a2+b2=±2
(1)上述解答过程错在哪里?为什么?
(2)请你用上述方法分解因式:(a+b)2-14(a+b)+49
24.当我们利用2种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图2,可得等式: .
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=12,ab+bc+ac=47,求a2+b2+c2的值;
(3)利用图3中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b)
25.(阅读材料)把形如ax2+bx+c的二次三项式(或其一部分)经过适当变形配成完全平方式的方法叫配方法,配方法在因式分解、证明恒等式、利用a2≥0求代数式最值等问题中都有广泛应用.
例如:利用配方法将x2﹣6x+8变形为a(x+m)2+n的形式,并把二次三项式分解因式.
配方:x2﹣6x+8
=x2﹣6x+32﹣32+8
=(x﹣3)2﹣1
分解因式:x2﹣6x+8
=(x﹣3)2﹣1
=(x﹣3+1)(x﹣3﹣1)
=(x﹣2)(x﹣4)
(解决问题)根据以上材料,解答下列问题:
(1)利用配方法将多项式x2﹣4x﹣5化成a(x+m)2+n的形式.
(2)利用配方法把二次三项式x2﹣2x﹣35分解因式.
(3)若a、b、c分别是 ABC的三边,且a2+2b2+3c2﹣2ab﹣2b﹣6c+4=0,试判断 ABC的形状,并说明理由.
(4)求证:无论x,y取任何实数,代数式x2+y2+4x﹣6y+15的值恒为正数.
答案解析部分
1.C
2.C
3.A
4.D
5.D
6.C
7.B
8.C
9.7(a﹣3)(a+3)
10.5或﹣3
11.2
12.①④
13.
14.
15.;(3x-2)(x-1)
16.22018-1
17.(1)解:原式
(2)解:原式
18.(1)解:
=
=
=
=
(2)解:∵ ,
∴原式=
=
=
=
=
= ;
19.(1)解:原式
(2)解:原式
=3+7+11+15+19
=55
20.(1)解:原式
(2)解:原式
(3)解:原式
(4)解:原式 .
21.解:第二环节:x2y﹣4y﹣2x2+8
=(x2y﹣4y)﹣(2x2﹣8)
=y(x2﹣4)﹣2(x2﹣4)
=(y﹣2)(x2﹣4)
=(y﹣2)(x+2)(x﹣2)
b2+2ab=c2+2ac,
第三环节:
b2﹣c2﹣2ab﹣2ac=0,
(b+c)(b﹣c)+2a(b﹣c)=0,
(2a+b+c)(b﹣c)=0,
∵2a+b+c≠0,
∴b﹣c=0,
即b=c,
所以,△ABC是等腰三角形
22.证明:∵3n+2-2n+2+3n-2n
=3n 32-2n 22+3n-2n
=3n(32+1)-2n(22+1)
=10 3n-10 2n-1
=10(3n-2n-1).
∴3n+2-2n+2+3n-2n能被10整除.
23.(1)解:错误:设(a2+b2)2=m,应注意m≥0,且a2+b2≥0,所以由(m-4)2=0,解得m=4由(a2+b2)2=4,得a2+b2=2.
(2)解:设a+b=m,则原式可化为m2-14m+49,即(m-7)2.
∴(a+b)2-14(a+b)+49=(a+b-7)2.
24.(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)解:∵a+b+c=12,ab+bc+ac=47,
∴a2+b2+c2=(a+b+c)2﹣2(ab+ac+bc)=144﹣94=50;
故答案为:50
(3)解:根据题意作图如下:
25.(1)解:x2﹣4x﹣5
=x2﹣4x+22﹣22﹣5
=(x﹣2)2﹣9.
(2)x2﹣2x﹣35
=x2﹣2x+1﹣1﹣35
=(x﹣1)2﹣62
=(x﹣1+6)(x﹣1﹣6)
=(x+5)(x﹣7).
(3)△ABC为等边三角形,理由如下:
∵a2+2b2+3c2﹣2ab﹣2b﹣6c+4=0,
∴(a2﹣2ab+b2)+(b2﹣2b+1)+3(c2﹣2c+1)=0,
∴(a﹣b)2+(b﹣1)2+3(c﹣1)2=0,
∵(a﹣b)2≥0,(b﹣1)2≥0,3(c﹣1)2≥0,
∴a﹣b=0,b﹣1=0,c﹣1=0,
∴a=b,b=1,c=1,
∴a=b=c,
∴△ABC为等边三角形.
(4)证明:x2+y2+4x﹣6y+15
=x2+4x+4+y2﹣6y+9+2
=(x+2)2+(y﹣3)2+2,
∵(x+2)2≥0,(y﹣3)2≥0,
∴(x+2)2+(y﹣3)2+2≥2,
∴代数式x2+y2+4x﹣6y+15的值恒为正数.
9 / 9
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
