2021-2022学年度初中数学北师大版八年级下册1.4角平分线 同步练习(word版、含答案)
文档属性
| 名称 | 2021-2022学年度初中数学北师大版八年级下册1.4角平分线 同步练习(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 344.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 14:50:21 | ||
图片预览


文档简介
初中数学北师大版八年级下册第一章第四节 角平分线 同步练习
一、单选题
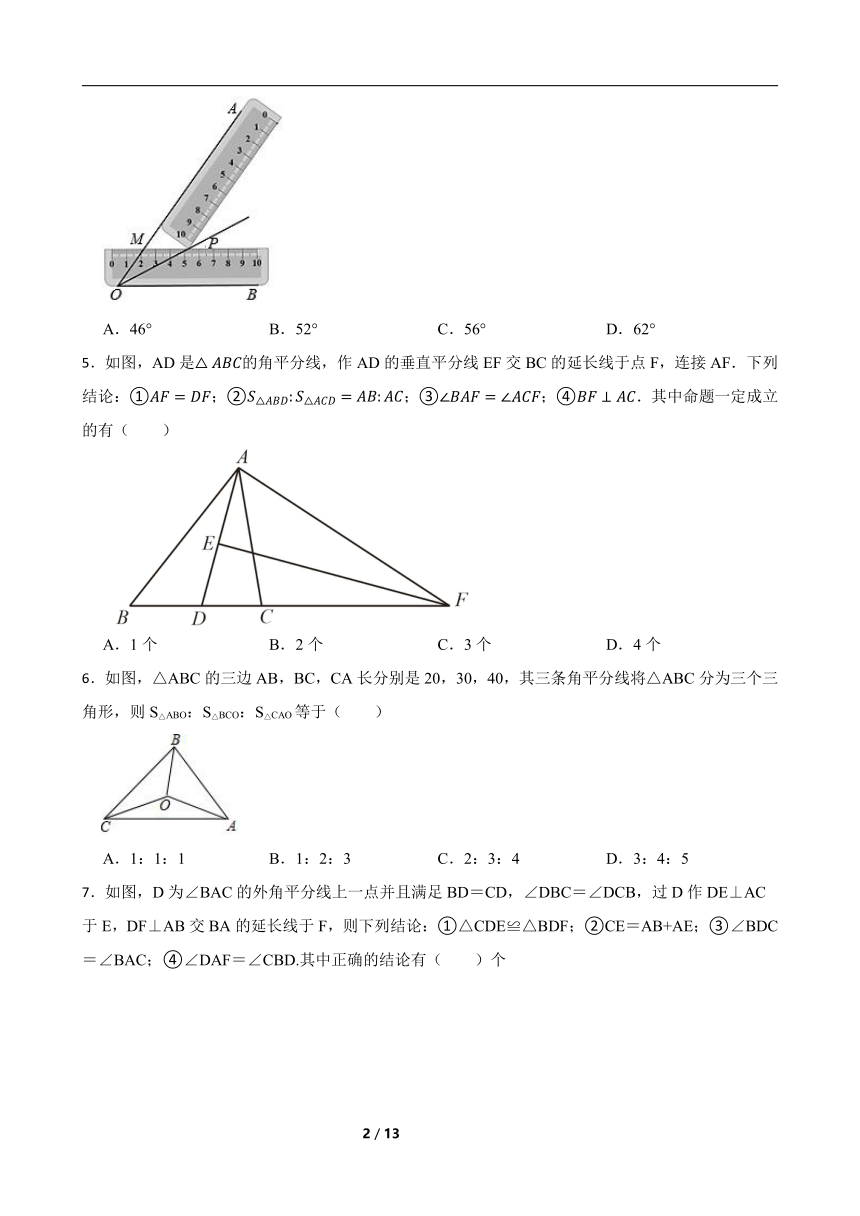
1.如图,在 中, , 是 的角平分线,若 ,则点 到 边的距离为( )
A.3 B. C.2 D.3
2.如图, 是 的平分线, 于点E, ,则 长是( )
A.3 B.4 C.6 D.5
3.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画圆弧,分别交AB、AC于点D、E,再分别以点D、E为圆心,大于DE长为半径画圆弧,两弧交于点F,作射线AF交边BC于点G,若CG=3,AB=10,则△ABG的面积是( )
A.3 B.10 C.15 D.30
4.用两把完全相同的长方形直尺按如图方式摆放,一把直尺压住射线OB交射线OA于点M,另一把直尺压住射线OA交第一把直尺于点P,作射线OP.若∠BOP=28°,则∠AMP的大小为( )
A.46° B.52° C.56° D.62°
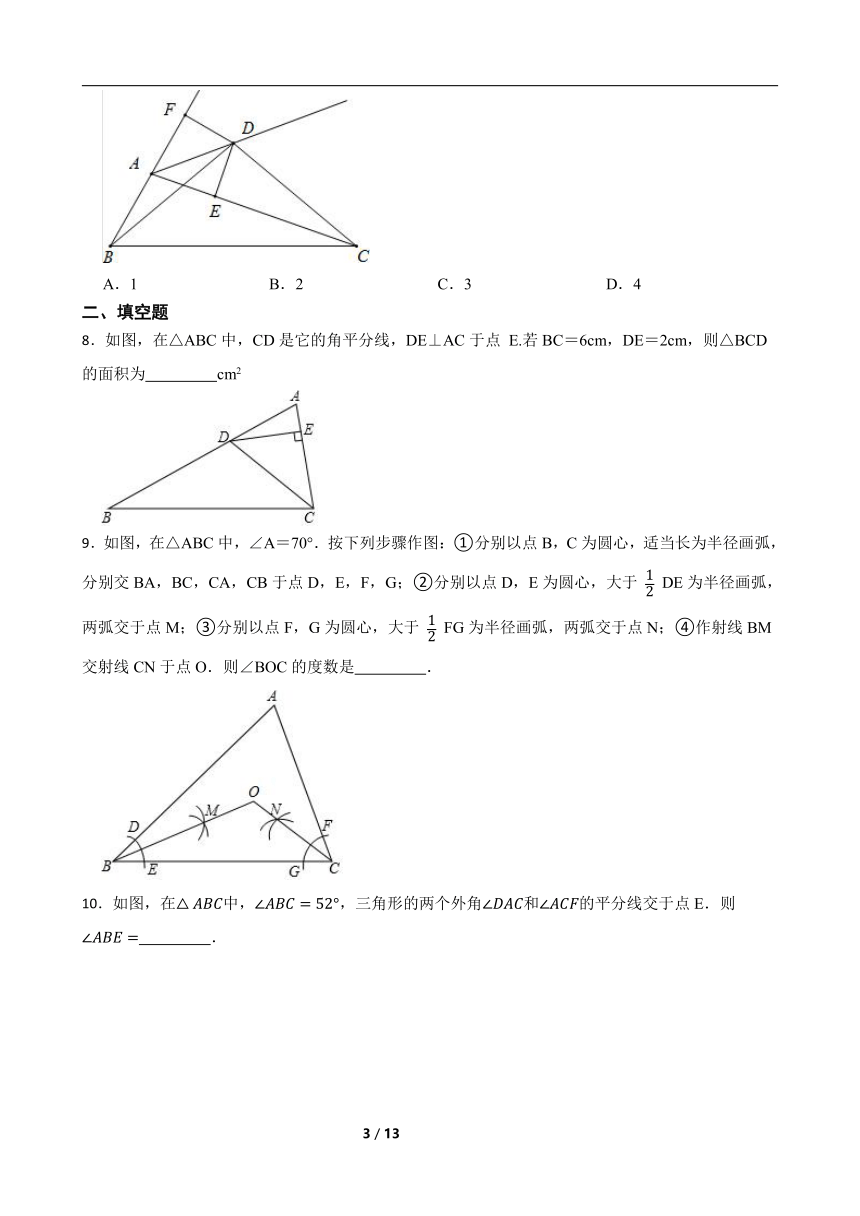
5.如图,AD是的角平分线,作AD的垂直平分线EF交BC的延长线于点F,连接AF.下列结论:①;②;③;④.其中命题一定成立的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
7.如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )个
A.1 B.2 C.3 D.4
二、填空题
8.如图,在△ABC中,CD是它的角平分线,DE⊥AC于点 E.若BC=6cm,DE=2cm,则△BCD的面积为 cm2
9.如图,在△ABC中,∠A=70°.按下列步骤作图:①分别以点B,C为圆心,适当长为半径画弧,分别交BA,BC,CA,CB于点D,E,F,G;②分别以点D,E为圆心,大于 DE为半径画弧,两弧交于点M;③分别以点F,G为圆心,大于 FG为半径画弧,两弧交于点N;④作射线BM交射线CN于点O.则∠BOC的度数是 .
10.如图,在中,,三角形的两个外角和的平分线交于点E.则 .
11.如图,AD平分∠BAC,DEAB,DF⊥AB.若AE=8,∠BAC=30°,则DF的长为 .
12.如图,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=2,△ABC的面积是 .
13.在x轴,y轴上分别截取OA,OB,使 ,再分别以点A,B为圆心,以大于 长为半径画弧,两弧交于点P.若点P的坐标为 ,则a的值为 .
14.如图,在 中, 和 的平分线 、 相交于点 , 交 于点 , 交 于点 ,过点 作 于点 ,则下列三个结论:① ;②当 时, ;③若 , ,则 .其中正确的是 .
三、作图题
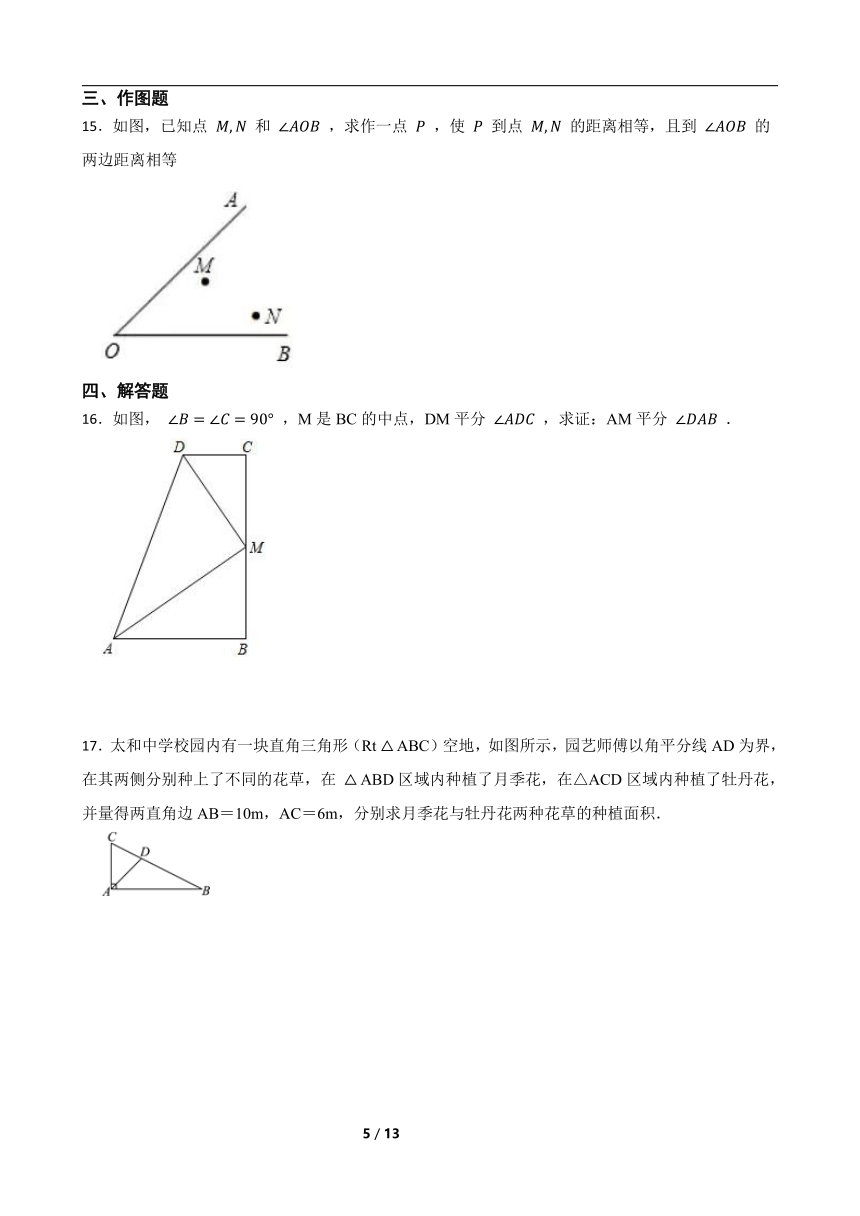
15.如图,已知点 和 ,求作一点 ,使 到点 的距离相等,且到 的两边距离相等
四、解答题
16.如图, ,M是BC的中点,DM平分 ,求证:AM平分 .
17.太和中学校园内有一块直角三角形(Rt ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在 ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.
18.已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长.
19.如图,在和中,,,, .
连接,交于点,连接.
(Ⅰ)求证:;
(Ⅱ)求的大小;
(Ⅲ)求证:
五、综合题
20.如图,已知△ABC的BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB的延长线于点F,EG⊥AC于点G,求证:
(1)BF=CG;
(2)AB+AC=2AG.
21.已知△ABC是等边三角形,D是BC边上的一动点,连结AD.
(1)如图1所示,若BD = 2,DC = 4,求AD的长.
(2)如图2所示,以AD为边作∠ADE =∠ADF =60°,分别交AB,AC于点E,F.
①小明通过观察、实验,提出猜想:在点D运动的过程中,始终有AE = AF,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的两种想法.
想法1:利用AD是∠EDF的平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的相关知识获证.
想法2:利用AD是∠EDF的平分线,构造△ADF的全等三角形,然后通过等腰三角形的相关知识获证
请你参考上面的想法,帮助小明证明AE =AF(一种方法即可).
②小聪在小明的基础上继续进行思考,发现:四边形AEDF的面积与AD的长存在一定的关系.若用S表示四边形AEDF的面积,x表示AD的长,请你直接写出S与x之间的函数表达式.
答案解析部分
1.A
2.A
3.C
4.C
5.C
6.C
7.D
8.6
9.125°
10.26°
11.4
12.20
13.3
14.①②
15.解:∵P点到点M、点N的距离相等,
∴P点一定在MN的垂直平分线上,
∵P点到 的两边距离相等,
∴P点一定在 的角平分线上.
即作MN的垂直平分线,再作 的角平分线,交点即为点P.
作图如下:
16.证明:如图,过点M作ME⊥AD于F,
∵∠C=90°,DM平分∠ADC,
∴ME=MC,
∵M是BC的中点,
∴BM=CM,
∴BM=EM,
又∵∠B=90°,
∴点M在∠BAD的平分线上,
∴AM平分∠DAB.
17.解:过点 分别作 , 是垂足.
由 ,得 , ,
是 的平分线,
.
18.解:如图,连接AP、CP,
∵BP平分∠ABC,PD⊥AB,PE⊥BC,
∴∠PBD=∠PBE,∠PDB=∠PEC=90°,PD=PE,
在△BPD和△BPE中,
,
∴△BPD≌△BPE(AAS),
∴BD=BE,
又∵BE=10cm,AB=6cm,
∴AD=BD﹣AB=BE﹣AB=4cm,
∵PQ垂直平分AC,
∴PA=PC,
在RT△PAD和RT△PCE中,
,
∴RT△PAD≌RT△PCE(HL),
∴CE=AD=4cm.
19.解:(Ⅰ)证明∵,
∴,即.
∵,,
∴≌.∴
(Ⅱ)如图,由(Ⅰ)可得.
∵,∴.
∴.
(Ⅲ)证明:如图,过分别作,,垂足分别为点,.
∵≌,∴.∴.
∵,∴.
∴ 点在的平分线上.∴.
20.(1)证明:连接BE、EC,
∵ED⊥BC,
D为BC中点,
∴BE=EC,
∵EF⊥AB,EG⊥AG,
且AE平分∠FAG,
∴FE=EG,
在Rt△BFE和Rt△CGE中,
,
∴Rt△BFE≌Rt△CGE (HL),
∴BF=CG;
(2)解:在Rt△AFE与Rt△AGE中,
,
∴Rt△AFE≌Rt△AGE,
∴AG=AF,
∴AB+AC=AB+AG+CG=AB+AG+BF=AG+AF=2AG.
21.(1)解:如图,过点A作BC的垂线AG,交BC于点G,
∵BD=2,DC=4,
∴BC=6.
∵△ABC是等边三角形,AGBC,
∴AB=BC=6,BG=BC=3,
∴DG=BG-BD=3-2=1,
∴AG=,AD=.
(2)解:①想法1:如图,过A作AMDF于点M,作AHDE,交DE的延长线于点H,
∵AD平分∠EDF,AHDE,AMDF,
∴AH=AM.
∵∠ADE=∠ADF=60°,
∴∠EDF=120°.
∵∠AED+∠AFD+∠BAC+∠EDF=360°,
∴∠AED+∠AFD=180°,且∠AED+∠AEH=180°,
∴∠AEH=∠AFD且AH=AM,∠H=∠AMF=90°,
∴Rt△AHE≌Rt△AMF,
∴AE=AF.
想法2:延长DE至N,使DN=DF.
∵DN=DF,AD=AD,∠ADE=∠ADF=60°,
∴△ADN≌△ADF,
∴AN=AF,∠AFD=∠N.
∵∠ADE=∠ADF=60°,
∴∠EDF=120°.
∵∠AED+∠AFD+∠BAC+∠EDF=360°,
∴∠AED+∠AFD=180°且∠AED+∠AEN=180°,
∴∠AEN=∠AFD,
∴∠AEN=∠N,
∴AN=AE=AF.
②
13 / 13
一、单选题
1.如图,在 中, , 是 的角平分线,若 ,则点 到 边的距离为( )
A.3 B. C.2 D.3
2.如图, 是 的平分线, 于点E, ,则 长是( )
A.3 B.4 C.6 D.5
3.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画圆弧,分别交AB、AC于点D、E,再分别以点D、E为圆心,大于DE长为半径画圆弧,两弧交于点F,作射线AF交边BC于点G,若CG=3,AB=10,则△ABG的面积是( )
A.3 B.10 C.15 D.30
4.用两把完全相同的长方形直尺按如图方式摆放,一把直尺压住射线OB交射线OA于点M,另一把直尺压住射线OA交第一把直尺于点P,作射线OP.若∠BOP=28°,则∠AMP的大小为( )
A.46° B.52° C.56° D.62°
5.如图,AD是的角平分线,作AD的垂直平分线EF交BC的延长线于点F,连接AF.下列结论:①;②;③;④.其中命题一定成立的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
7.如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )个
A.1 B.2 C.3 D.4
二、填空题
8.如图,在△ABC中,CD是它的角平分线,DE⊥AC于点 E.若BC=6cm,DE=2cm,则△BCD的面积为 cm2
9.如图,在△ABC中,∠A=70°.按下列步骤作图:①分别以点B,C为圆心,适当长为半径画弧,分别交BA,BC,CA,CB于点D,E,F,G;②分别以点D,E为圆心,大于 DE为半径画弧,两弧交于点M;③分别以点F,G为圆心,大于 FG为半径画弧,两弧交于点N;④作射线BM交射线CN于点O.则∠BOC的度数是 .
10.如图,在中,,三角形的两个外角和的平分线交于点E.则 .
11.如图,AD平分∠BAC,DEAB,DF⊥AB.若AE=8,∠BAC=30°,则DF的长为 .
12.如图,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=2,△ABC的面积是 .
13.在x轴,y轴上分别截取OA,OB,使 ,再分别以点A,B为圆心,以大于 长为半径画弧,两弧交于点P.若点P的坐标为 ,则a的值为 .
14.如图,在 中, 和 的平分线 、 相交于点 , 交 于点 , 交 于点 ,过点 作 于点 ,则下列三个结论:① ;②当 时, ;③若 , ,则 .其中正确的是 .
三、作图题
15.如图,已知点 和 ,求作一点 ,使 到点 的距离相等,且到 的两边距离相等
四、解答题
16.如图, ,M是BC的中点,DM平分 ,求证:AM平分 .
17.太和中学校园内有一块直角三角形(Rt ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在 ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.
18.已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长.
19.如图,在和中,,,, .
连接,交于点,连接.
(Ⅰ)求证:;
(Ⅱ)求的大小;
(Ⅲ)求证:
五、综合题
20.如图,已知△ABC的BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB的延长线于点F,EG⊥AC于点G,求证:
(1)BF=CG;
(2)AB+AC=2AG.
21.已知△ABC是等边三角形,D是BC边上的一动点,连结AD.
(1)如图1所示,若BD = 2,DC = 4,求AD的长.
(2)如图2所示,以AD为边作∠ADE =∠ADF =60°,分别交AB,AC于点E,F.
①小明通过观察、实验,提出猜想:在点D运动的过程中,始终有AE = AF,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的两种想法.
想法1:利用AD是∠EDF的平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的相关知识获证.
想法2:利用AD是∠EDF的平分线,构造△ADF的全等三角形,然后通过等腰三角形的相关知识获证
请你参考上面的想法,帮助小明证明AE =AF(一种方法即可).
②小聪在小明的基础上继续进行思考,发现:四边形AEDF的面积与AD的长存在一定的关系.若用S表示四边形AEDF的面积,x表示AD的长,请你直接写出S与x之间的函数表达式.
答案解析部分
1.A
2.A
3.C
4.C
5.C
6.C
7.D
8.6
9.125°
10.26°
11.4
12.20
13.3
14.①②
15.解:∵P点到点M、点N的距离相等,
∴P点一定在MN的垂直平分线上,
∵P点到 的两边距离相等,
∴P点一定在 的角平分线上.
即作MN的垂直平分线,再作 的角平分线,交点即为点P.
作图如下:
16.证明:如图,过点M作ME⊥AD于F,
∵∠C=90°,DM平分∠ADC,
∴ME=MC,
∵M是BC的中点,
∴BM=CM,
∴BM=EM,
又∵∠B=90°,
∴点M在∠BAD的平分线上,
∴AM平分∠DAB.
17.解:过点 分别作 , 是垂足.
由 ,得 , ,
是 的平分线,
.
18.解:如图,连接AP、CP,
∵BP平分∠ABC,PD⊥AB,PE⊥BC,
∴∠PBD=∠PBE,∠PDB=∠PEC=90°,PD=PE,
在△BPD和△BPE中,
,
∴△BPD≌△BPE(AAS),
∴BD=BE,
又∵BE=10cm,AB=6cm,
∴AD=BD﹣AB=BE﹣AB=4cm,
∵PQ垂直平分AC,
∴PA=PC,
在RT△PAD和RT△PCE中,
,
∴RT△PAD≌RT△PCE(HL),
∴CE=AD=4cm.
19.解:(Ⅰ)证明∵,
∴,即.
∵,,
∴≌.∴
(Ⅱ)如图,由(Ⅰ)可得.
∵,∴.
∴.
(Ⅲ)证明:如图,过分别作,,垂足分别为点,.
∵≌,∴.∴.
∵,∴.
∴ 点在的平分线上.∴.
20.(1)证明:连接BE、EC,
∵ED⊥BC,
D为BC中点,
∴BE=EC,
∵EF⊥AB,EG⊥AG,
且AE平分∠FAG,
∴FE=EG,
在Rt△BFE和Rt△CGE中,
,
∴Rt△BFE≌Rt△CGE (HL),
∴BF=CG;
(2)解:在Rt△AFE与Rt△AGE中,
,
∴Rt△AFE≌Rt△AGE,
∴AG=AF,
∴AB+AC=AB+AG+CG=AB+AG+BF=AG+AF=2AG.
21.(1)解:如图,过点A作BC的垂线AG,交BC于点G,
∵BD=2,DC=4,
∴BC=6.
∵△ABC是等边三角形,AGBC,
∴AB=BC=6,BG=BC=3,
∴DG=BG-BD=3-2=1,
∴AG=,AD=.
(2)解:①想法1:如图,过A作AMDF于点M,作AHDE,交DE的延长线于点H,
∵AD平分∠EDF,AHDE,AMDF,
∴AH=AM.
∵∠ADE=∠ADF=60°,
∴∠EDF=120°.
∵∠AED+∠AFD+∠BAC+∠EDF=360°,
∴∠AED+∠AFD=180°,且∠AED+∠AEH=180°,
∴∠AEH=∠AFD且AH=AM,∠H=∠AMF=90°,
∴Rt△AHE≌Rt△AMF,
∴AE=AF.
想法2:延长DE至N,使DN=DF.
∵DN=DF,AD=AD,∠ADE=∠ADF=60°,
∴△ADN≌△ADF,
∴AN=AF,∠AFD=∠N.
∵∠ADE=∠ADF=60°,
∴∠EDF=120°.
∵∠AED+∠AFD+∠BAC+∠EDF=360°,
∴∠AED+∠AFD=180°且∠AED+∠AEN=180°,
∴∠AEN=∠AFD,
∴∠AEN=∠N,
∴AN=AE=AF.
②
13 / 13
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
