空间向量与立体几何(A卷)单元复习-2021-2022学年高二下学期数学人教A版(2019)选择性必修第一册(Word含答案解析)
文档属性
| 名称 | 空间向量与立体几何(A卷)单元复习-2021-2022学年高二下学期数学人教A版(2019)选择性必修第一册(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 10:50:03 | ||
图片预览



文档简介
(11)空间向量与立体几何(A卷)
——2021-2022学年高二数学(理科)人教A版
1.空间直角坐标系中,已知,,则线段AB的中点坐标为( )
A. B. C. D.
2.在四棱锥中,底面ABCD是正方形,E为PD的中点,若,,,则用基底表示向量为( )
A. B.
C. D.
3.已知,,且,则( )
A., B.,
C., D.,
4.在棱长为2的正四面体ABCD中,点M满足,点N满足,当AM、BN最短时,( )
A. B. C. D.
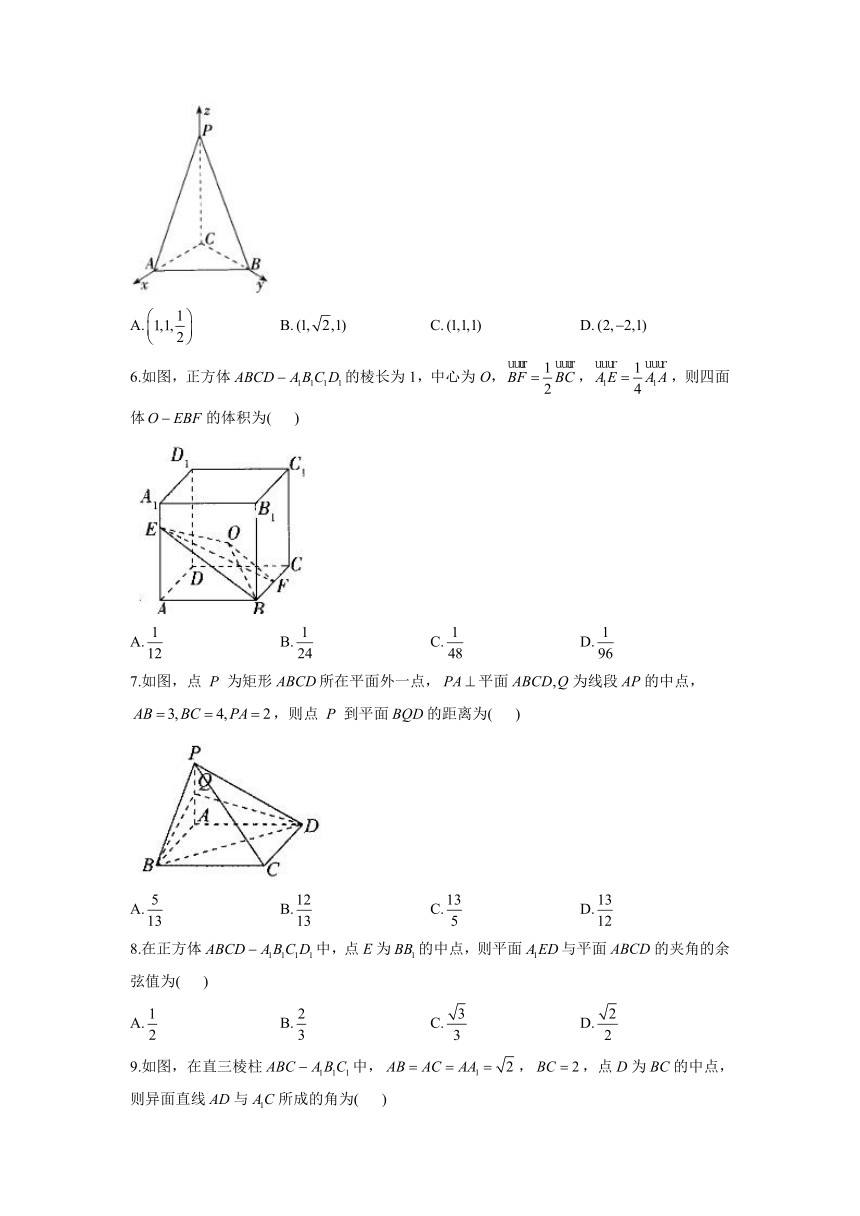
5.在三棱锥中,CP,CA,CB两两互相垂直,,,建立如图所示的空间直角坐标系,则下列向量是平面PAB的一个法向量的是( )
A. B. C. D.
6.如图,正方体的棱长为1,中心为O,,,则四面体的体积为( )
A. B. C. D.
7.如图,点为矩形所在平面外一点,平面为线段的中点,,则点到平面的距离为( )
A. B. C. D.
8.在正方体中,点E为的中点,则平面与平面ABCD的夹角的余弦值为( )
A. B. C. D.
9.如图,在直三棱柱中,,,点D为BC的中点,则异面直线AD与所成的角为( )
A. B. C. D.
10.如图,N为正方形ABCD的中心,为正三角形,平面平面ABCD,M是线段ED的中点,则下列结论正确的是( )
A.二面角是直二面角
B.直线BM,EN是异面直线
C.
D.直线EN与平面MCB所成角的正弦值为
11.如图,在和中,B是EF的中点,,,.若,则与的夹角的余弦值为__________.
12.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的三棱锥称为鳖曘.如图,在鳖曘中,平面ABC,,M为PC的中点,则点P到平面MAB的距离为____________.
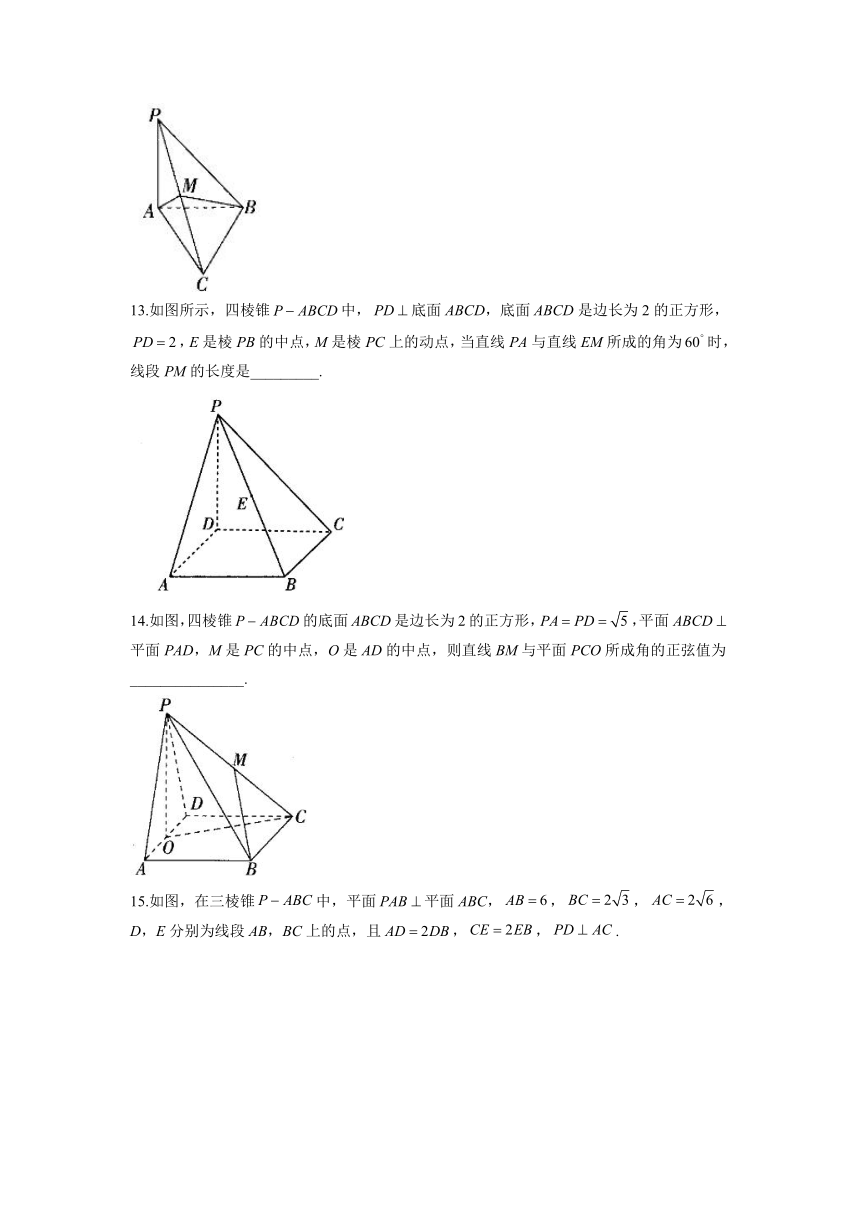
13.如图所示,四棱锥中,底面ABCD,底面ABCD是边长为2的正方形,,E是棱PB的中点,M是棱PC上的动点,当直线PA与直线EM所成的角为时,线段PM的长度是_________.
14.如图,四棱锥的底面ABCD是边长为2的正方形,,平面平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值为_______________.
15.如图,在三棱锥中,平面平面ABC,,,,D,E分别为线段AB,BC上的点,且,,.
(1)求证:平面ABC;
(2)若直线PA与平面ABC所成的角为,求平面PAC与平面PDE所成的二面角的大小.
答案以及解析
1.答案:D
解析:设中点坐标为,根据中点坐标公式得,,.故选D.
2.答案:C
解析:连接BD,E为PD的中点,.故选C.
3.答案:B
解析:由题意可得,,.
,
,使,
得解得故选B.
4.答案:A
解析:由共面向量定理和共线向量定理可知,平面BCD,直线AC,当AM、BN最短时,平面BCD,,
所以M为的中心,N为AC的中点,
此时,,,
平面BCD,平面BCD,
,
.
又,
.故选A.
5.答案:A
解析:由题意可得,,,则,,设平面PAB的一个法向量为,
由得
令,则,,.
又,平面PAB的一个法向量为.故选A.
6.答案:D
解析:如图所示,以D为坐标原点,DA,DC,所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则,,,,因此,,,所以,,.
易得,所以.
设平面EBF的一个法向量为,则
令,得,
所以点O到平面EBF的距离为,所以四面体的体积.
7.答案:B
解析:如图,以为原点,分别以所在直线为轴、轴、轴建立空间直角坐标系,则,.
设平面的一个法向量为,则即
令,则.
点到平面的距离.
8.答案:B
解析:以A为原点,AB,AD,所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,设正方体的棱长为1,则,,,
,.
设平面的法向量为,则有即令,得 .
易得平面ABCD的一个法向量,,
即平面与平面ABCD的夹角的余弦值为.
9.答案:B
解析:解法一 取的中点,连接,.易证,故,所成的角就是AD,所成的角.,,D为BC的中点,,,,又,,,为直角三角形,,即异面直线AD与所成的角为,故选B.
解法二 易知AB,AC,两两垂直,以A为坐标原点,AB,AC,所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则,,,,,,,,即异面直线AD与所成的角为.故选B.
10.答案:D
解析:如图,构造长方体,则E是GH的中点.
在A中,二面角是直二面角,
二面角是锐二面角,故A错误;
在B中,连接BD,MN,则N是BD的中点,
,
BM与EN是相交直线,故B错误;
在C中,以C为原点,CD所在直线为x轴,CB所在直线为y轴,CG所在直线为z轴,建立如图所示的空间直角坐标系,
设,
则,,,,,,
,,
,CM与EN不垂直,故C错误;
在D中,,,,
设平面MCB的一个法向量为,
则
令,得,
设直线EN与平面MCB所成的角为,
则,
直线EN与平面MCB所成角的正弦值为,故D正确.故选D.
11.答案:
解析:由题意得,所以.由,可得.所以,即,所以.
12.答案:
解析:易知,,,故以B为坐标原点,BA,BC所在直线分别为x轴,y轴,过点B且与平面ABC垂直的直线为z轴,建立如图所示的空间直角坐标系,
则,,,,由M为PC的中点可得,则,,.
设为平面MBA的一个法向量,
则即
令,则,所以,所以点P到平面MAB的距离.
13.答案:
解析:以D为坐标原点,直线DA为x轴,直线DC为y轴,直线DP为z轴,建立如图所示的空间直角坐标系Dxyz.
依题意,知,,,.是棱PB的中点,点E的坐标为.设,
则,,
解得.,.
14.答案:
解析:取BC的中点E,连接OE,易得OA,OE,OP两两互相垂直,故以O为坐标原点,,,的方向分别为x轴,y轴,z轴正方向,建立如图所示的空间直角坐标系,
则,,,,,
因此,,,
设平面PCO的一个法向量为,
则即
令,得,
因此直线BM与平面PCO所成角的正弦值为.
15.答案:(1)见解析
(2)
解析:(1)因为,,,所以,
所以,可得,
又因为,
所以,
可得,
又因为,所以,所以,
因为平面平面ABC,平面平面,面ABC,
所以平面PAB,因为面PAB,所以,
因为,,所以平面ABC.
(2)由(1)知DC,DB,DP两两垂直,如图分别以DC,DB,DP所在的直线为x,y,z轴建立空间直角坐标系,
因为直线PA与平面ABC所成的角为,即,所以,
则,,,,
所以,,,
因为,,所以,
由(1)知,所以,
又平面ABC,面ABC,所以,
因为,所以平面PDE,
所以为平面PDE的一个法向量,
设平面PAC的法向量为,
由,令,得,,
所以为平面PAC的一个法向量.
所以,
所以平面PAC与平面PDE所成的锐二面角的余弦值为,
故平面PAC与平面PDE所成的锐二面角为.
——2021-2022学年高二数学(理科)人教A版
1.空间直角坐标系中,已知,,则线段AB的中点坐标为( )
A. B. C. D.
2.在四棱锥中,底面ABCD是正方形,E为PD的中点,若,,,则用基底表示向量为( )
A. B.
C. D.
3.已知,,且,则( )
A., B.,
C., D.,
4.在棱长为2的正四面体ABCD中,点M满足,点N满足,当AM、BN最短时,( )
A. B. C. D.
5.在三棱锥中,CP,CA,CB两两互相垂直,,,建立如图所示的空间直角坐标系,则下列向量是平面PAB的一个法向量的是( )
A. B. C. D.
6.如图,正方体的棱长为1,中心为O,,,则四面体的体积为( )
A. B. C. D.
7.如图,点为矩形所在平面外一点,平面为线段的中点,,则点到平面的距离为( )
A. B. C. D.
8.在正方体中,点E为的中点,则平面与平面ABCD的夹角的余弦值为( )
A. B. C. D.
9.如图,在直三棱柱中,,,点D为BC的中点,则异面直线AD与所成的角为( )
A. B. C. D.
10.如图,N为正方形ABCD的中心,为正三角形,平面平面ABCD,M是线段ED的中点,则下列结论正确的是( )
A.二面角是直二面角
B.直线BM,EN是异面直线
C.
D.直线EN与平面MCB所成角的正弦值为
11.如图,在和中,B是EF的中点,,,.若,则与的夹角的余弦值为__________.
12.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的三棱锥称为鳖曘.如图,在鳖曘中,平面ABC,,M为PC的中点,则点P到平面MAB的距离为____________.
13.如图所示,四棱锥中,底面ABCD,底面ABCD是边长为2的正方形,,E是棱PB的中点,M是棱PC上的动点,当直线PA与直线EM所成的角为时,线段PM的长度是_________.
14.如图,四棱锥的底面ABCD是边长为2的正方形,,平面平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值为_______________.
15.如图,在三棱锥中,平面平面ABC,,,,D,E分别为线段AB,BC上的点,且,,.
(1)求证:平面ABC;
(2)若直线PA与平面ABC所成的角为,求平面PAC与平面PDE所成的二面角的大小.
答案以及解析
1.答案:D
解析:设中点坐标为,根据中点坐标公式得,,.故选D.
2.答案:C
解析:连接BD,E为PD的中点,.故选C.
3.答案:B
解析:由题意可得,,.
,
,使,
得解得故选B.
4.答案:A
解析:由共面向量定理和共线向量定理可知,平面BCD,直线AC,当AM、BN最短时,平面BCD,,
所以M为的中心,N为AC的中点,
此时,,,
平面BCD,平面BCD,
,
.
又,
.故选A.
5.答案:A
解析:由题意可得,,,则,,设平面PAB的一个法向量为,
由得
令,则,,.
又,平面PAB的一个法向量为.故选A.
6.答案:D
解析:如图所示,以D为坐标原点,DA,DC,所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则,,,,因此,,,所以,,.
易得,所以.
设平面EBF的一个法向量为,则
令,得,
所以点O到平面EBF的距离为,所以四面体的体积.
7.答案:B
解析:如图,以为原点,分别以所在直线为轴、轴、轴建立空间直角坐标系,则,.
设平面的一个法向量为,则即
令,则.
点到平面的距离.
8.答案:B
解析:以A为原点,AB,AD,所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,设正方体的棱长为1,则,,,
,.
设平面的法向量为,则有即令,得 .
易得平面ABCD的一个法向量,,
即平面与平面ABCD的夹角的余弦值为.
9.答案:B
解析:解法一 取的中点,连接,.易证,故,所成的角就是AD,所成的角.,,D为BC的中点,,,,又,,,为直角三角形,,即异面直线AD与所成的角为,故选B.
解法二 易知AB,AC,两两垂直,以A为坐标原点,AB,AC,所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则,,,,,,,,即异面直线AD与所成的角为.故选B.
10.答案:D
解析:如图,构造长方体,则E是GH的中点.
在A中,二面角是直二面角,
二面角是锐二面角,故A错误;
在B中,连接BD,MN,则N是BD的中点,
,
BM与EN是相交直线,故B错误;
在C中,以C为原点,CD所在直线为x轴,CB所在直线为y轴,CG所在直线为z轴,建立如图所示的空间直角坐标系,
设,
则,,,,,,
,,
,CM与EN不垂直,故C错误;
在D中,,,,
设平面MCB的一个法向量为,
则
令,得,
设直线EN与平面MCB所成的角为,
则,
直线EN与平面MCB所成角的正弦值为,故D正确.故选D.
11.答案:
解析:由题意得,所以.由,可得.所以,即,所以.
12.答案:
解析:易知,,,故以B为坐标原点,BA,BC所在直线分别为x轴,y轴,过点B且与平面ABC垂直的直线为z轴,建立如图所示的空间直角坐标系,
则,,,,由M为PC的中点可得,则,,.
设为平面MBA的一个法向量,
则即
令,则,所以,所以点P到平面MAB的距离.
13.答案:
解析:以D为坐标原点,直线DA为x轴,直线DC为y轴,直线DP为z轴,建立如图所示的空间直角坐标系Dxyz.
依题意,知,,,.是棱PB的中点,点E的坐标为.设,
则,,
解得.,.
14.答案:
解析:取BC的中点E,连接OE,易得OA,OE,OP两两互相垂直,故以O为坐标原点,,,的方向分别为x轴,y轴,z轴正方向,建立如图所示的空间直角坐标系,
则,,,,,
因此,,,
设平面PCO的一个法向量为,
则即
令,得,
因此直线BM与平面PCO所成角的正弦值为.
15.答案:(1)见解析
(2)
解析:(1)因为,,,所以,
所以,可得,
又因为,
所以,
可得,
又因为,所以,所以,
因为平面平面ABC,平面平面,面ABC,
所以平面PAB,因为面PAB,所以,
因为,,所以平面ABC.
(2)由(1)知DC,DB,DP两两垂直,如图分别以DC,DB,DP所在的直线为x,y,z轴建立空间直角坐标系,
因为直线PA与平面ABC所成的角为,即,所以,
则,,,,
所以,,,
因为,,所以,
由(1)知,所以,
又平面ABC,面ABC,所以,
因为,所以平面PDE,
所以为平面PDE的一个法向量,
设平面PAC的法向量为,
由,令,得,,
所以为平面PAC的一个法向量.
所以,
所以平面PAC与平面PDE所成的锐二面角的余弦值为,
故平面PAC与平面PDE所成的锐二面角为.
