1.2.1任意角的三角函数课件
文档属性
| 名称 | 1.2.1任意角的三角函数课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 534.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-11 00:00:00 | ||
图片预览


文档简介
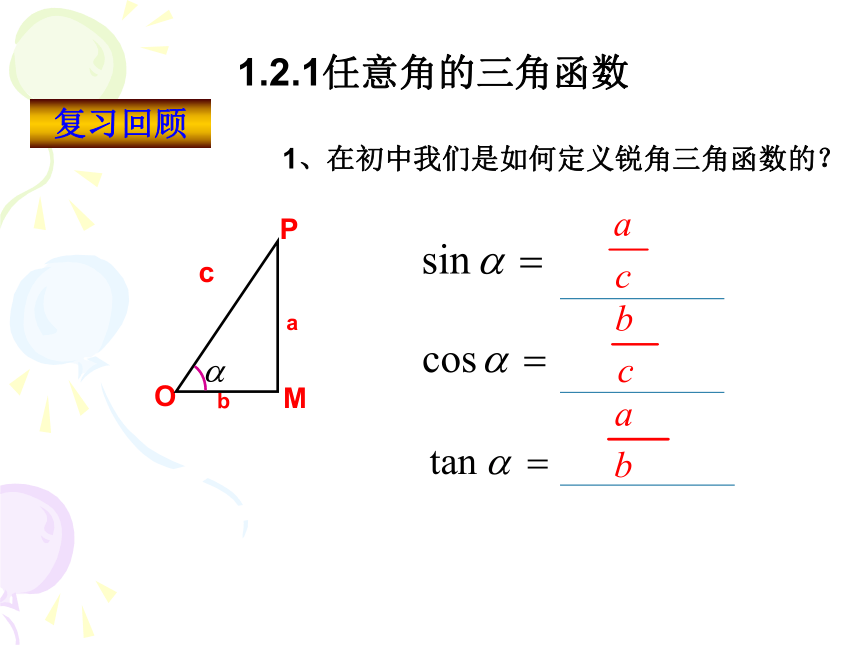
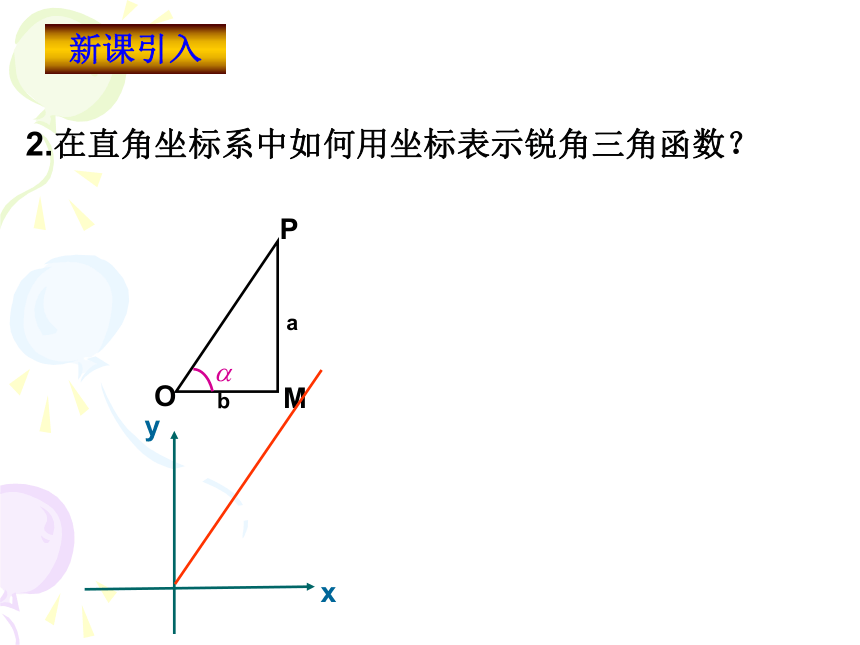
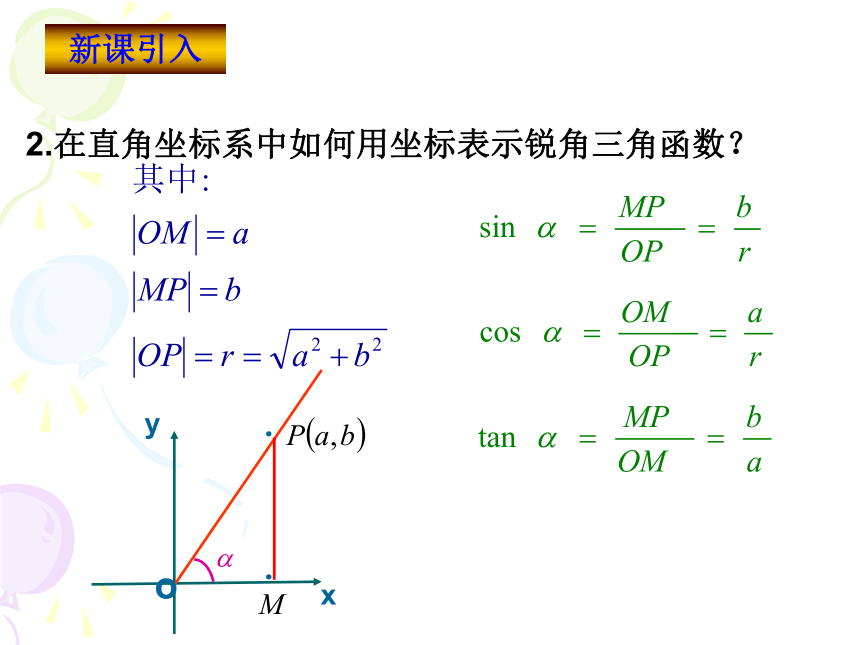
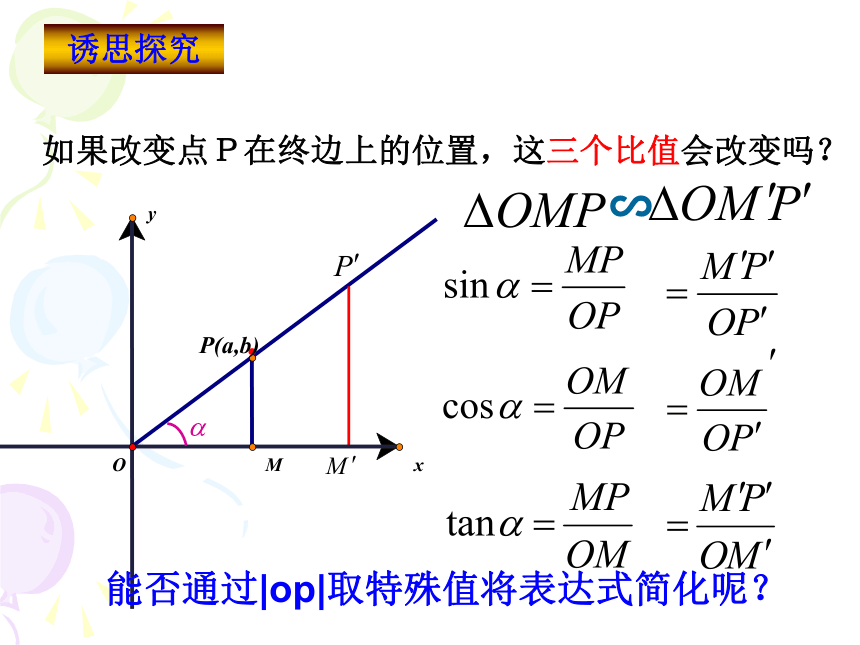
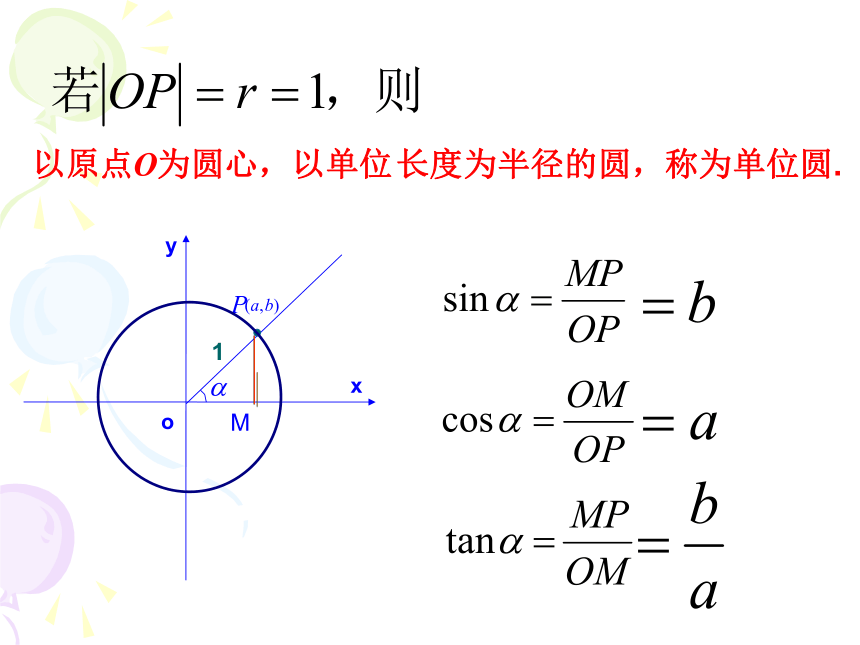
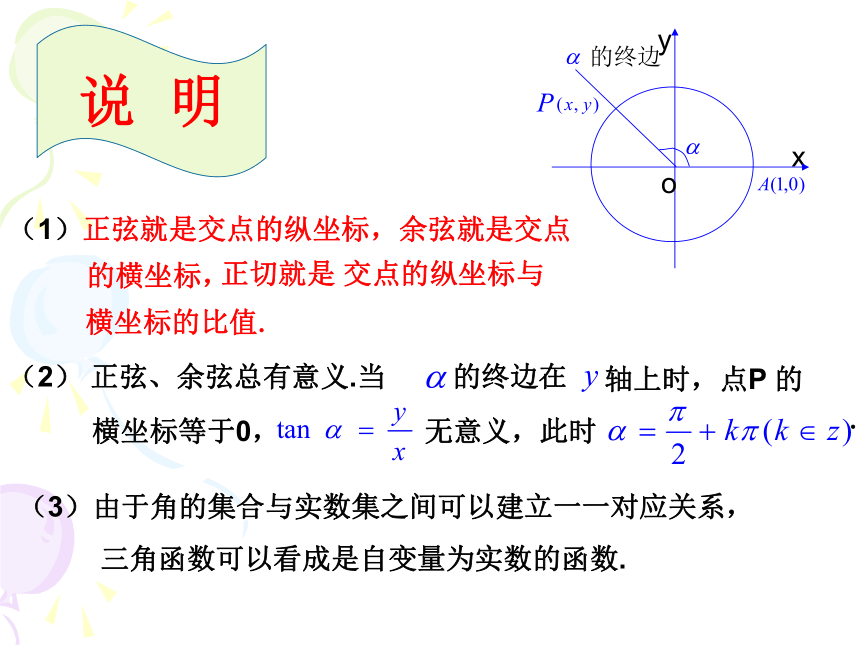
课件27张PPT。1.2.1任意角的三角函数 1、在初中我们是如何定义锐角三角函数的? 1.2.1任意角的三角函数复习回顾 yx2.在直角坐标系中如何用坐标表示锐角三角函数?新课引入 yx2.在直角坐标系中如何用坐标表示锐角三角函数?﹒﹒o新课引入如果改变点P在终边上的位置,这三个比值会改变吗?﹒∽MOyxP(a,b)诱思探究能否通过|op|取特殊值将表达式简化呢?3.任意角的三角函数定义 设 是一个任意角,它的终边与单位圆交于点 那么:(1) 叫做 的正弦,记作 ,即 ; (2) 叫做 的余弦,记作 ,即 ; (3) 叫做 的正切,记作 ,即 所以,正弦,余弦,正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将他们称为三角函数.使比值有意义的角的集合
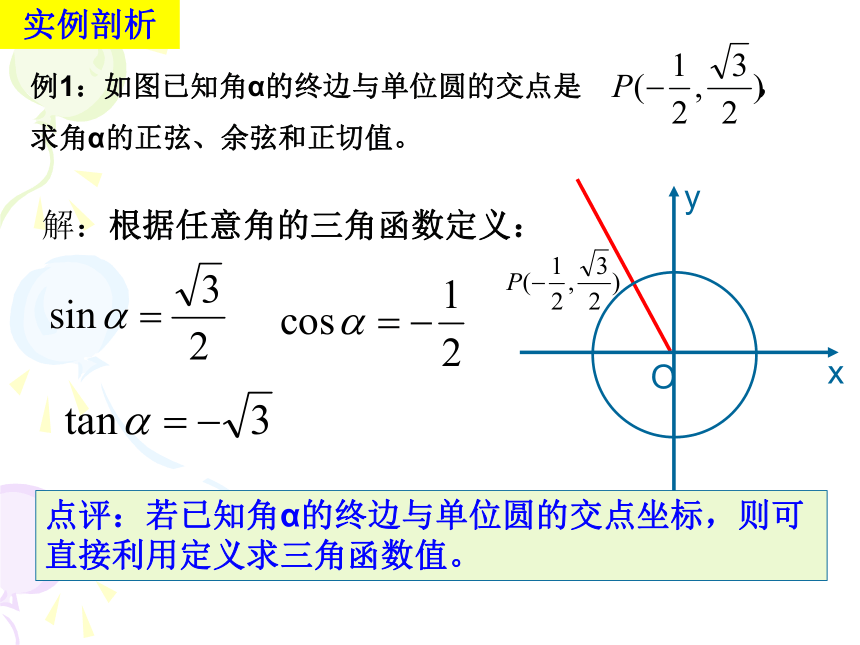
即为三角函数的定义域.例1:如图已知角α的终边与单位圆的交点是 , 求角α的正弦、余弦和正切值。解:根据任意角的三角函数定义:点评:若已知角α的终边与单位圆的交点坐标,则可直接利用定义求三角函数值。实例剖析例2 求 的正弦、余弦和正切值.的终边与单位圆的交点坐标为 所以 思考:若把角 改为 呢? ,, 实例剖析点评:若已知角α的大小,可求出角α终边与单位圆的交点,
然后再利用定义求三角函数值。例3 已知角 的终边经过点 ,求角 的正弦、余弦和正切值 .解:由已知可得设角 的终边与单位圆交于 ,分别过点 、 作 轴的垂线 、\ 于是, ∽
设角 是一个任意角, 是终边上的任意一点,
点 与原点的距离那么① 叫做 的正弦,即 ② 叫做 的余弦,即③ 叫做 的正弦,即 任意角 的三角函数值仅与 有关,而与点 在角的终边上的位置无关.定义推广:于是,练习 1、已知角 的终边过点 ,
求 的三个三角函数值.解:由已知可得:证明: 因为①式 成立,所以 角的终边可能位于第三 或第四象限,也可能位于y 轴的非正半轴上; 又因为②式 成立,所以角 的终边可能位于第一或第三象限. 因为①②式都成立,所以角 的终边只能位于第三象限.
于是角 为第三象限角.反过来请同学们自己证明.RR口诀“一全正, 二正弦,三正切,四余弦.”+--+--++-+-思考:如果两个角的终边相同,那么这两个角的
同一三角函数值有何关系? 利用公式一,可以把求任意角的三角函数值,转化为
求 角的三角函数值 . ?例4 确定下列三角函数值的符号:
(1) (2) (3)
解:(1)因为 是第三象限角,所以 ;(2)因为 = ,
而 是第一象限角,所以 ;练习 确定下列三角函数值的符号 (3)因为 是第四象限角,所以 .例5 求下列三角函数值:
(1) (2) 解:(1) 练习 求下列三角函数值 (2)1. 有向线段的概念:带有方向的线段叫有向线段 ;
有向线段的数值由其长度大小和方向来决定。 如在数轴上,|OA|=3,|OB|=3 我们把轴上的向量
分别叫做α的余弦线、正弦线和正切线.sinα=ON,
cosα=OM,
与α角的终边(或其反向延长线)相交于点T(或T ’),则tanα=AT(或AT ’)2. 三角函数线例1.分别作出 、 、 的正弦线、余弦线、正切线。例2.比较大小:
(1) sin1和sin1.5; (2) cos1和cos1.5;
(3) tan2和tan3.解:由三角函数线得sin1cos1.5tan2x1=30o, x2=150o.特殊情况:
① 当角的终边在x轴上时,点P与点M重合,点T与点A重合,这时正弦线与正切线都变成了一点,数量为零,而余弦线OM=1或-1。
② 当角的终边在y轴上时,正弦线MP=1或-1余弦线变成了一点,它表示的数量为零,正切线不存在。 三角函数的概念
三角函数的定义域及三角函数值在各象限的符号
诱导公式一
给定任意一个角α,都能在单位圆中作出它的正弦线、余弦线、正切线
三角函数线的位置 例4. 已知α∈(0, ),试证明sinα<α
即为三角函数的定义域.例1:如图已知角α的终边与单位圆的交点是 , 求角α的正弦、余弦和正切值。解:根据任意角的三角函数定义:点评:若已知角α的终边与单位圆的交点坐标,则可直接利用定义求三角函数值。实例剖析例2 求 的正弦、余弦和正切值.的终边与单位圆的交点坐标为 所以 思考:若把角 改为 呢? ,, 实例剖析点评:若已知角α的大小,可求出角α终边与单位圆的交点,
然后再利用定义求三角函数值。例3 已知角 的终边经过点 ,求角 的正弦、余弦和正切值 .解:由已知可得设角 的终边与单位圆交于 ,分别过点 、 作 轴的垂线 、\ 于是, ∽
设角 是一个任意角, 是终边上的任意一点,
点 与原点的距离那么① 叫做 的正弦,即 ② 叫做 的余弦,即③ 叫做 的正弦,即 任意角 的三角函数值仅与 有关,而与点 在角的终边上的位置无关.定义推广:于是,练习 1、已知角 的终边过点 ,
求 的三个三角函数值.解:由已知可得:证明: 因为①式 成立,所以 角的终边可能位于第三 或第四象限,也可能位于y 轴的非正半轴上; 又因为②式 成立,所以角 的终边可能位于第一或第三象限. 因为①②式都成立,所以角 的终边只能位于第三象限.
于是角 为第三象限角.反过来请同学们自己证明.RR口诀“一全正, 二正弦,三正切,四余弦.”+--+--++-+-思考:如果两个角的终边相同,那么这两个角的
同一三角函数值有何关系? 利用公式一,可以把求任意角的三角函数值,转化为
求 角的三角函数值 . ?例4 确定下列三角函数值的符号:
(1) (2) (3)
解:(1)因为 是第三象限角,所以 ;(2)因为 = ,
而 是第一象限角,所以 ;练习 确定下列三角函数值的符号 (3)因为 是第四象限角,所以 .例5 求下列三角函数值:
(1) (2) 解:(1) 练习 求下列三角函数值 (2)1. 有向线段的概念:带有方向的线段叫有向线段 ;
有向线段的数值由其长度大小和方向来决定。 如在数轴上,|OA|=3,|OB|=3 我们把轴上的向量
分别叫做α的余弦线、正弦线和正切线.sinα=ON,
cosα=OM,
与α角的终边(或其反向延长线)相交于点T(或T ’),则tanα=AT(或AT ’)2. 三角函数线例1.分别作出 、 、 的正弦线、余弦线、正切线。例2.比较大小:
(1) sin1和sin1.5; (2) cos1和cos1.5;
(3) tan2和tan3.解:由三角函数线得sin1
① 当角的终边在x轴上时,点P与点M重合,点T与点A重合,这时正弦线与正切线都变成了一点,数量为零,而余弦线OM=1或-1。
② 当角的终边在y轴上时,正弦线MP=1或-1余弦线变成了一点,它表示的数量为零,正切线不存在。 三角函数的概念
三角函数的定义域及三角函数值在各象限的符号
诱导公式一
给定任意一个角α,都能在单位圆中作出它的正弦线、余弦线、正切线
三角函数线的位置 例4. 已知α∈(0, ),试证明sinα<α
