华东师大版七年级下册数学 10.3.2 旋转的特征 课件(共16张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 10.3.2 旋转的特征 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 132.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
旋转的特征
学习目标:
1、掌握旋转的特征并灵活运用其特征;
2、能按要求作出简单平面图形旋转后的图形,能说出旋转作图的作法。
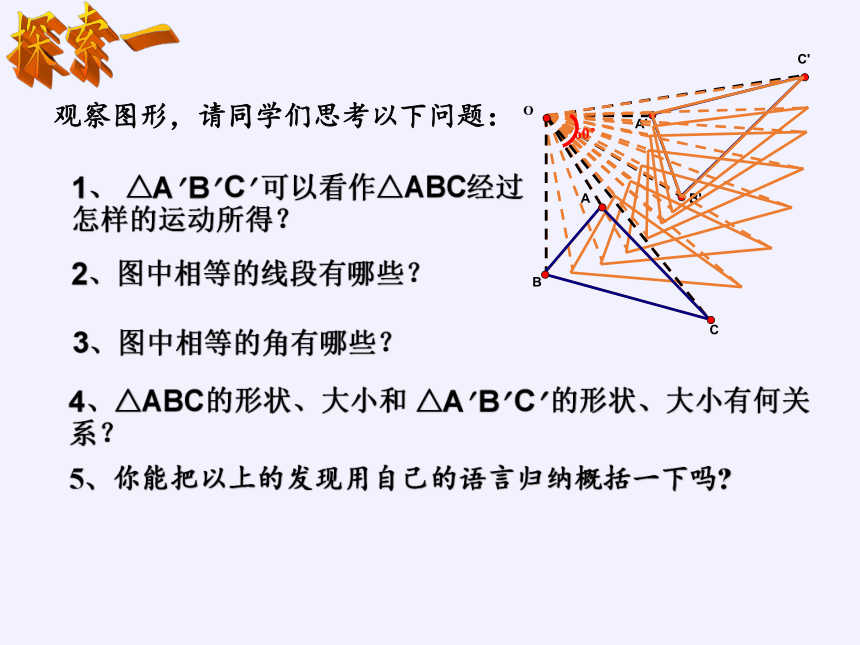
观察图形,请同学们思考以下问题:
A'
B'
C'
O
60°
B
C
A
探索一
1、 △A B C 可以看作△ABC经过
怎样的运动所得?
2、图中相等的线段有哪些?
3、图中相等的角有哪些?
4、△ABC的形状、大小和 △A B C 的形状、大小有何关系?
5、你能把以上的发现用自己的语言归纳概括一下吗
1、图形中的每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度;(对应点与旋转中心所连线段的夹角都是旋转角)
2、对应点到旋转中心的距离相等;
3、旋转前后对应线段相等,对应角相等;旋转不改变图形的形状和大小。
旋转的特征
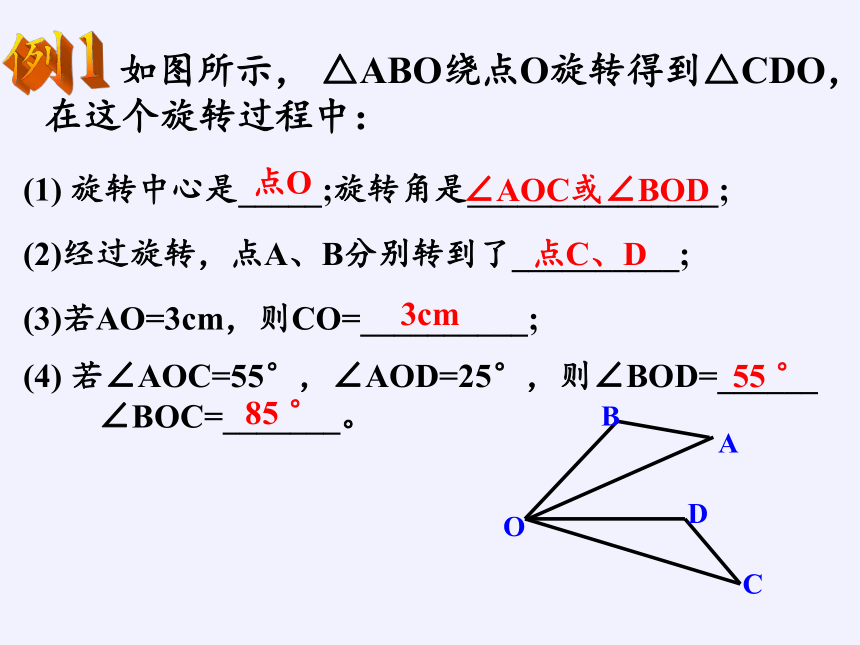
如图所示, △ABO绕点O旋转得到△CDO,在这个旋转过程中:
(1) 旋转中心是_____;旋转角是_______________;
(2)经过旋转,点A、B分别转到了__________;
(3)若AO=3cm,则CO=__________;
(4) 若∠AOC=55°,∠AOD=25°,则∠BOD=______
∠BOC=_______。
A
B
C
D
O
点O
∠AOC或∠BOD
点C、D
3cm
55 °
85 °
例1
A
B
C
O
A
B
C
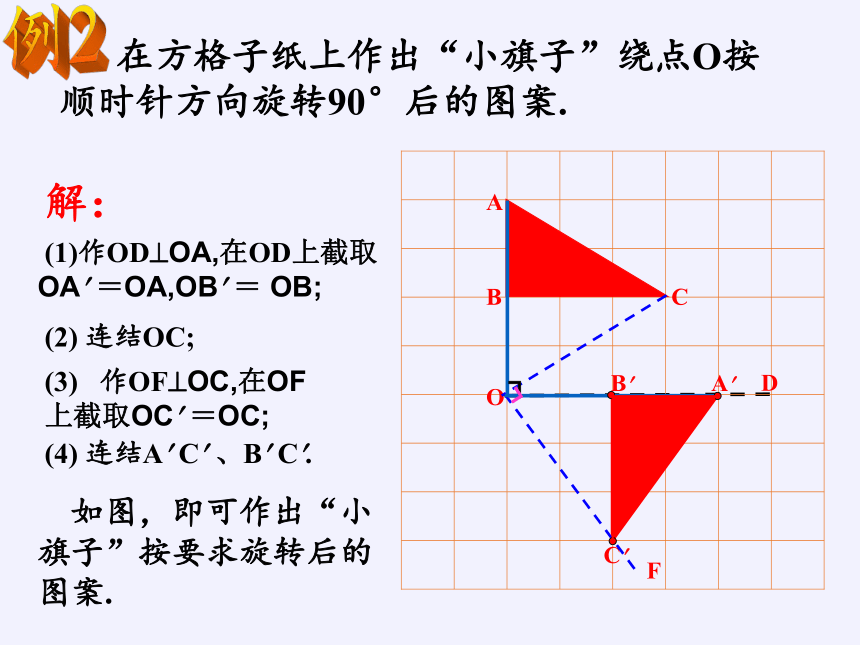
在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案.
(1)作OD OA,在OD上截取OA =OA,OB = OB;
(2) 连结OC;
(3) 作OF OC,在OF上截取OC =OC;
(4) 连结A C 、B C .
┓
┓
如图,即可作出“小旗子”按要求旋转后的图案.
解:
例2
D
F
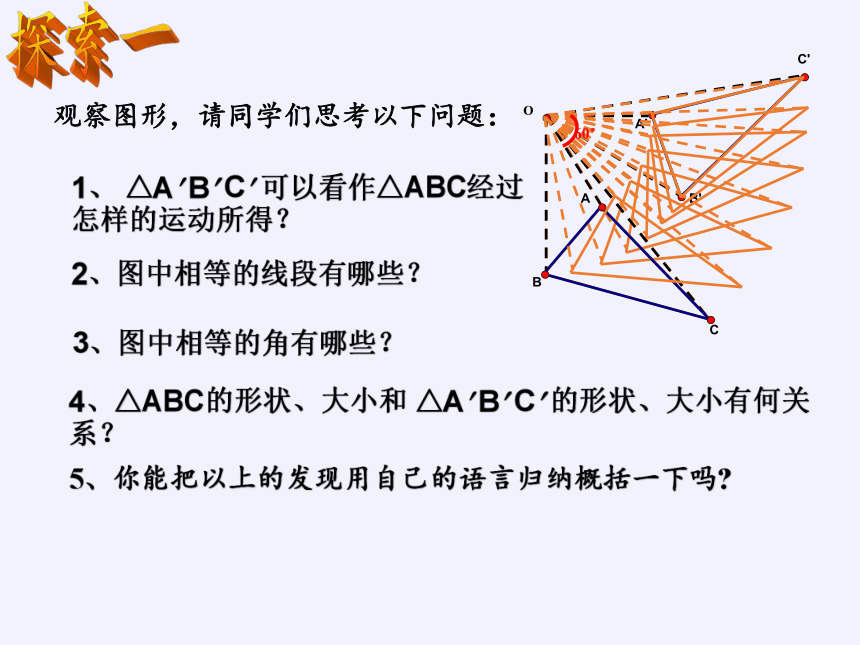
观察图形,请同学们思考以下问题:
A'
B'
C'
O
60°
B
C
A
探索一
1、 △A B C 可以看作△ABC经过
怎样的运动所得?
2、图中相等的线段有哪些?
3、图中相等的角有哪些?
4、△ABC的形状、大小和 △A B C 的形状、大小有何关系?
5、你能把以上的发现用自己的语言归纳概括一下吗
1、如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后到达△CAE的位置。问:
A
E
C
B
D
(1)旋转中心是_____,旋转的度数是____
(2)若已知∠DCB=200,则∠CDB=_______, ∠AEC=____, ∠BAE=____
(3)如果连结DE,那么
△DCE是________三角形。
点C
90°
115°
90°
等腰直角
115°
练习
A、45°,90° B、90°,45° C、60°,30° D、30°,60°
A
2、 如图1,ΔABC和ΔADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2;两次旋转的角度分别为( ).
3、画出△ABC绕点C逆时针旋转90°后的图形
(书本上122页练习3)
A
B
C
A’
B’
如图,在正方形ABCD中, △ABE旋转后能与△ ADF重合,说出线段AF与BE的关系,并说明理由。
解:相等且互相垂直,证明如下:
∵ △ ABE旋转后能与△ ADF重合
∴AF=BE且∠1=∠2,
又∠2+∠3=90°
∴∠1+∠3=90°
∴∠AOE=90°即AF⊥BE
∴AF=BE 且AF⊥BE
拓展:
这节课你有什么收获?
小结
如图是一个直角三角形的苗圃,有正方形花坛和两块直角三角形的草皮组成,如果两个直角三角形的两条斜边长分别为3米和6米,问草皮的面积是多少?
思考题
A
B
C
D
E
F
3米
6米
如图 :通过旋转图形,我们可以把两个直角三角形拼结成一个直角三角形,而这个直角三角形的两条直角边正好是3米和6米。
A
B
C
D
E
F
作业:书本122页练习第2题.
作业
谢 谢
旋转的特征
学习目标:
1、掌握旋转的特征并灵活运用其特征;
2、能按要求作出简单平面图形旋转后的图形,能说出旋转作图的作法。
观察图形,请同学们思考以下问题:
A'
B'
C'
O
60°
B
C
A
探索一
1、 △A B C 可以看作△ABC经过
怎样的运动所得?
2、图中相等的线段有哪些?
3、图中相等的角有哪些?
4、△ABC的形状、大小和 △A B C 的形状、大小有何关系?
5、你能把以上的发现用自己的语言归纳概括一下吗
1、图形中的每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度;(对应点与旋转中心所连线段的夹角都是旋转角)
2、对应点到旋转中心的距离相等;
3、旋转前后对应线段相等,对应角相等;旋转不改变图形的形状和大小。
旋转的特征
如图所示, △ABO绕点O旋转得到△CDO,在这个旋转过程中:
(1) 旋转中心是_____;旋转角是_______________;
(2)经过旋转,点A、B分别转到了__________;
(3)若AO=3cm,则CO=__________;
(4) 若∠AOC=55°,∠AOD=25°,则∠BOD=______
∠BOC=_______。
A
B
C
D
O
点O
∠AOC或∠BOD
点C、D
3cm
55 °
85 °
例1
A
B
C
O
A
B
C
在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案.
(1)作OD OA,在OD上截取OA =OA,OB = OB;
(2) 连结OC;
(3) 作OF OC,在OF上截取OC =OC;
(4) 连结A C 、B C .
┓
┓
如图,即可作出“小旗子”按要求旋转后的图案.
解:
例2
D
F
观察图形,请同学们思考以下问题:
A'
B'
C'
O
60°
B
C
A
探索一
1、 △A B C 可以看作△ABC经过
怎样的运动所得?
2、图中相等的线段有哪些?
3、图中相等的角有哪些?
4、△ABC的形状、大小和 △A B C 的形状、大小有何关系?
5、你能把以上的发现用自己的语言归纳概括一下吗
1、如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后到达△CAE的位置。问:
A
E
C
B
D
(1)旋转中心是_____,旋转的度数是____
(2)若已知∠DCB=200,则∠CDB=_______, ∠AEC=____, ∠BAE=____
(3)如果连结DE,那么
△DCE是________三角形。
点C
90°
115°
90°
等腰直角
115°
练习
A、45°,90° B、90°,45° C、60°,30° D、30°,60°
A
2、 如图1,ΔABC和ΔADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2;两次旋转的角度分别为( ).
3、画出△ABC绕点C逆时针旋转90°后的图形
(书本上122页练习3)
A
B
C
A’
B’
如图,在正方形ABCD中, △ABE旋转后能与△ ADF重合,说出线段AF与BE的关系,并说明理由。
解:相等且互相垂直,证明如下:
∵ △ ABE旋转后能与△ ADF重合
∴AF=BE且∠1=∠2,
又∠2+∠3=90°
∴∠1+∠3=90°
∴∠AOE=90°即AF⊥BE
∴AF=BE 且AF⊥BE
拓展:
这节课你有什么收获?
小结
如图是一个直角三角形的苗圃,有正方形花坛和两块直角三角形的草皮组成,如果两个直角三角形的两条斜边长分别为3米和6米,问草皮的面积是多少?
思考题
A
B
C
D
E
F
3米
6米
如图 :通过旋转图形,我们可以把两个直角三角形拼结成一个直角三角形,而这个直角三角形的两条直角边正好是3米和6米。
A
B
C
D
E
F
作业:书本122页练习第2题.
作业
谢 谢
