华东师大版七年级下册数学 9.1.2 三角形的内角和与外角和 课件(共11张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 9.1.2 三角形的内角和与外角和 课件(共11张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 874.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 17:11:55 | ||
图片预览


文档简介
(共11张PPT)
三角形的内角与外角和
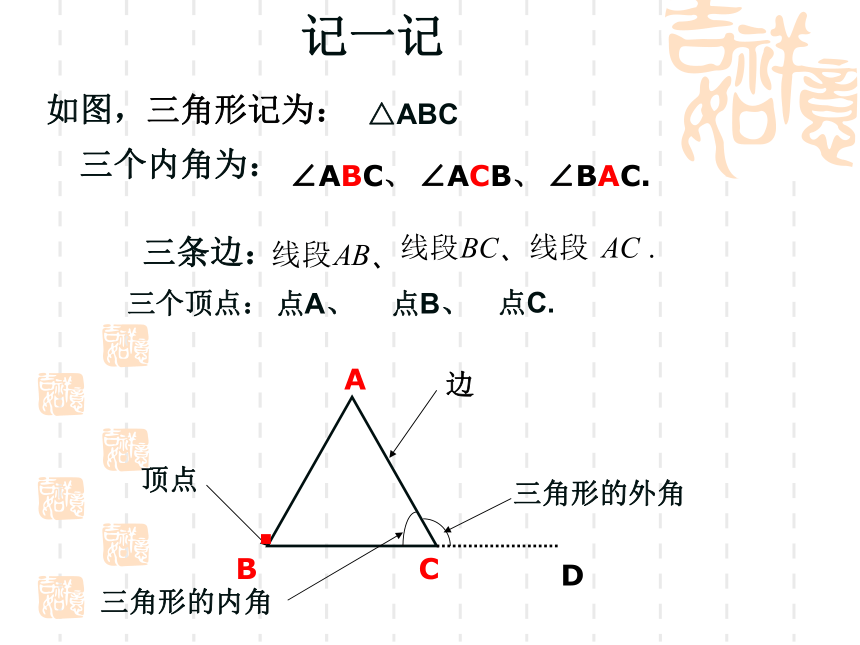
记一记
如图,三角形记为:
三个内角为:
∠ABC、
∠ACB、
∠BAC.
A
B
C
D
顶点
边
三角形的内角
三角形的外角
·
三条边:
三个顶点:
点A、
点B、
点C.
△ABC
A
C
B
E
F
G
M
N
K
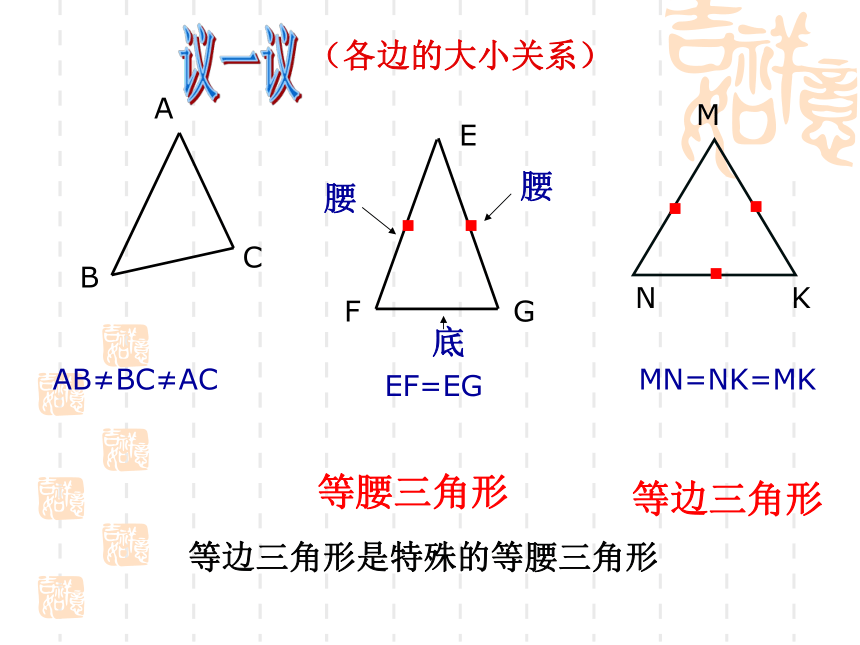
AB≠BC≠AC
EF=EG
MN=NK=MK
等腰三角形
等边三角形
腰
腰
底
等边三角形是特殊的等腰三角形
·
·
·
·
·
(各边的大小关系)
·
(中点)
·
·
三条中线
∟
∟
∟
三条高
三条角平分线
A
B
C
D
∟
中点
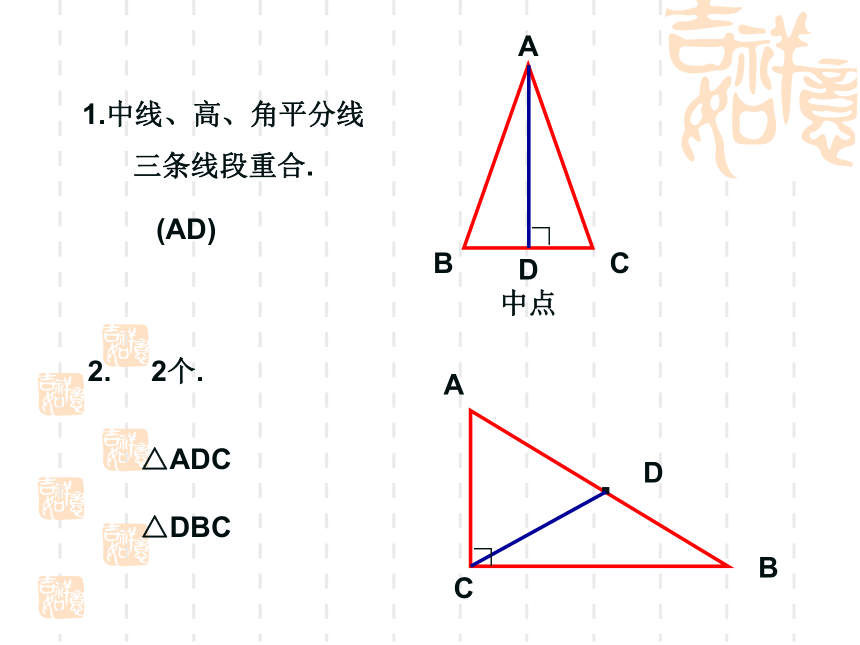
1.中线、高、角平分线
三条线段重合.
2. 2个.
·
(AD)
A
B
C
D
△ADC
△DBC
∟
C
A
B
1
3
2
(1)内角有几个
想一想
(3)有多少个外角
(4)与内角∠BAC相邻的外角有几个
它们是什么关系
(2)怎样画△ABC的外角
△ABC中:
4
5
6
(3个)
(6个)
(2个)
(相等)
三角形中内角的一边与另一边的反向延长线所成的角叫做三角形的外角.
C
A
B
D
E
F
如图, ∠1, ∠2, ∠3是△ABC的外角.
1
3
2
三角形的外角:
∠1+∠2+∠3=
三角形的外角和等于
C
A
B
1
3
2
所以∠1+∠2+∠3=
三角形的外角和等于
推理:
∠1+
∠2+
∠3+
∠4
4
∠5
∠6
6
5
三式相加可以得到
∠1+∠2+∠3
+∠4+∠5+∠6
而∠4+∠5+∠6
外角
相邻内角
不相邻内角
A
D
B
1
2
三角形的外角性质:
∠1= ∠A +∠B
∠1 + ∠2 =
外角
相邻内角
∠A +∠B + ∠2 =
1.三角形的一个外角等于与它不相邻的两个内角的和;
2.三角形的一个外角大于任何与它不相邻的两个内角.
∠1﹥ ∠A,
∠1 ﹥ ∠B.
求下列各图中∠1的度数.
练一练
1
①
②
③
1
1
∠1=
∠1=
∠1=
三角形的内角和等于
三角形的外角和等于
例题
如图,D是△ABC的BC边上一点, ∠B= ∠BAD, ∠ADC=80°, ∠BAC=70°.求(1) ∠B的度数;(2) ∠C的度数.
A
B
C
D
80°
70°
解
(1)因为∠ADC是△ABD的外角,所以
∠ADC=
∠B+ ∠BAD
=80°
又
∠B= ∠BAD
所以
∠B=
80°
=40°
(2)在△ABC中,因为
∠B+ ∠BAC+ ∠C
=180°
所以
∠C = 180° - ∠B - ∠BAC
= 180° - 40° - 70°
=70°
答: ∠B为40°, ∠C 为70°.
三角形的内角与外角和
记一记
如图,三角形记为:
三个内角为:
∠ABC、
∠ACB、
∠BAC.
A
B
C
D
顶点
边
三角形的内角
三角形的外角
·
三条边:
三个顶点:
点A、
点B、
点C.
△ABC
A
C
B
E
F
G
M
N
K
AB≠BC≠AC
EF=EG
MN=NK=MK
等腰三角形
等边三角形
腰
腰
底
等边三角形是特殊的等腰三角形
·
·
·
·
·
(各边的大小关系)
·
(中点)
·
·
三条中线
∟
∟
∟
三条高
三条角平分线
A
B
C
D
∟
中点
1.中线、高、角平分线
三条线段重合.
2. 2个.
·
(AD)
A
B
C
D
△ADC
△DBC
∟
C
A
B
1
3
2
(1)内角有几个
想一想
(3)有多少个外角
(4)与内角∠BAC相邻的外角有几个
它们是什么关系
(2)怎样画△ABC的外角
△ABC中:
4
5
6
(3个)
(6个)
(2个)
(相等)
三角形中内角的一边与另一边的反向延长线所成的角叫做三角形的外角.
C
A
B
D
E
F
如图, ∠1, ∠2, ∠3是△ABC的外角.
1
3
2
三角形的外角:
∠1+∠2+∠3=
三角形的外角和等于
C
A
B
1
3
2
所以∠1+∠2+∠3=
三角形的外角和等于
推理:
∠1+
∠2+
∠3+
∠4
4
∠5
∠6
6
5
三式相加可以得到
∠1+∠2+∠3
+∠4+∠5+∠6
而∠4+∠5+∠6
外角
相邻内角
不相邻内角
A
D
B
1
2
三角形的外角性质:
∠1= ∠A +∠B
∠1 + ∠2 =
外角
相邻内角
∠A +∠B + ∠2 =
1.三角形的一个外角等于与它不相邻的两个内角的和;
2.三角形的一个外角大于任何与它不相邻的两个内角.
∠1﹥ ∠A,
∠1 ﹥ ∠B.
求下列各图中∠1的度数.
练一练
1
①
②
③
1
1
∠1=
∠1=
∠1=
三角形的内角和等于
三角形的外角和等于
例题
如图,D是△ABC的BC边上一点, ∠B= ∠BAD, ∠ADC=80°, ∠BAC=70°.求(1) ∠B的度数;(2) ∠C的度数.
A
B
C
D
80°
70°
解
(1)因为∠ADC是△ABD的外角,所以
∠ADC=
∠B+ ∠BAD
=80°
又
∠B= ∠BAD
所以
∠B=
80°
=40°
(2)在△ABC中,因为
∠B+ ∠BAC+ ∠C
=180°
所以
∠C = 180° - ∠B - ∠BAC
= 180° - 40° - 70°
=70°
答: ∠B为40°, ∠C 为70°.
