2021-2022学年苏科版八年级数学下册第9章中心对称图形-平行四边形单元测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册第9章中心对称图形-平行四边形单元测试(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览

文档简介
2021-2022学年苏科版八年级数学(下)第九单元《中心对称图形-平行四边形》2021年中考真题单元测试
一、选择题
1.(2021.徐州)下列图形,是轴对称图形但不是中心对称图形的是( )
A. B.
C. D.
2.(2021.苏州)如图,在平行四边形ABCD中,将△ABC沿着AC所在的直线得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是( )
A.1 B. C. D.
3.(2021.宿迁)如图,折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )
A. B.2 C. D.4
4.(2021.无锡)如图,D、E、F分别是△ABC各边中点,则以下说法错误的是( )
A.△BDE和△DCF的面积相等 B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形 D.若∠A=90°,则四边形AEDF是矩形
5.(2021.安徽)如图,在菱形ABCD中,,,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
6.(2021.青岛)如图,在四边形纸片ABCD中,AD∥BC,AB=10,∠B=60°,将纸片折叠,使点B落在AD边上的点G处,折痕为EF,若∠BFE=45°,则BF的长为( )
A.5 B.3 C.5 D.
7.(2021.成都)如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
8.(2021.遂宁)如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C恰好落在AB边上的F处,则CE的长是( )
A.1 B. C. D.
9.(2021.泰州).如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( )
A.2α B.90°﹣α C.45°+α D.90°﹣α
10.(2021.连云港)如图,将矩形纸片沿折叠后,点D、C分别落在点、的位置,的延长线交于点G,若,则等于( )
A. B. C. D.
11.(2021.丽水)如图,在Rt△ABC纸片中,∠ACB=90°,AC=4,BC=3,点D,E分别在AB,AC上,连结DE,将△ADE沿DE翻折,使点A的对应点F落在BC的延长线上,若FD平分∠EFB,则AD的长为( )
A. B. C. D.
12.(2021.重庆A)如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
二、填空题
13.(2021.徐州) 如图,四边形与均为矩形,点分别在线段上.若,矩形的周长为,则图中阴影部分的面积为___________.
14.(2021.扬州)如图,在 ABCD中,点E在AD上,且EC平分∠BED,若∠EBC=30°,BE=10,则 ABCD的面积为 .
15.(2021·苏州)如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为 .(结果保留根号)
16.(2021.盐城)如图,在矩形ABCD中,AB=3,AD=4,E、F分别是边BC、CD上一点,EF⊥AE,将△ECF沿EF翻折得△ECF,连接AC,当BE= 时,△AEC是以AE为腰的等腰三角形.
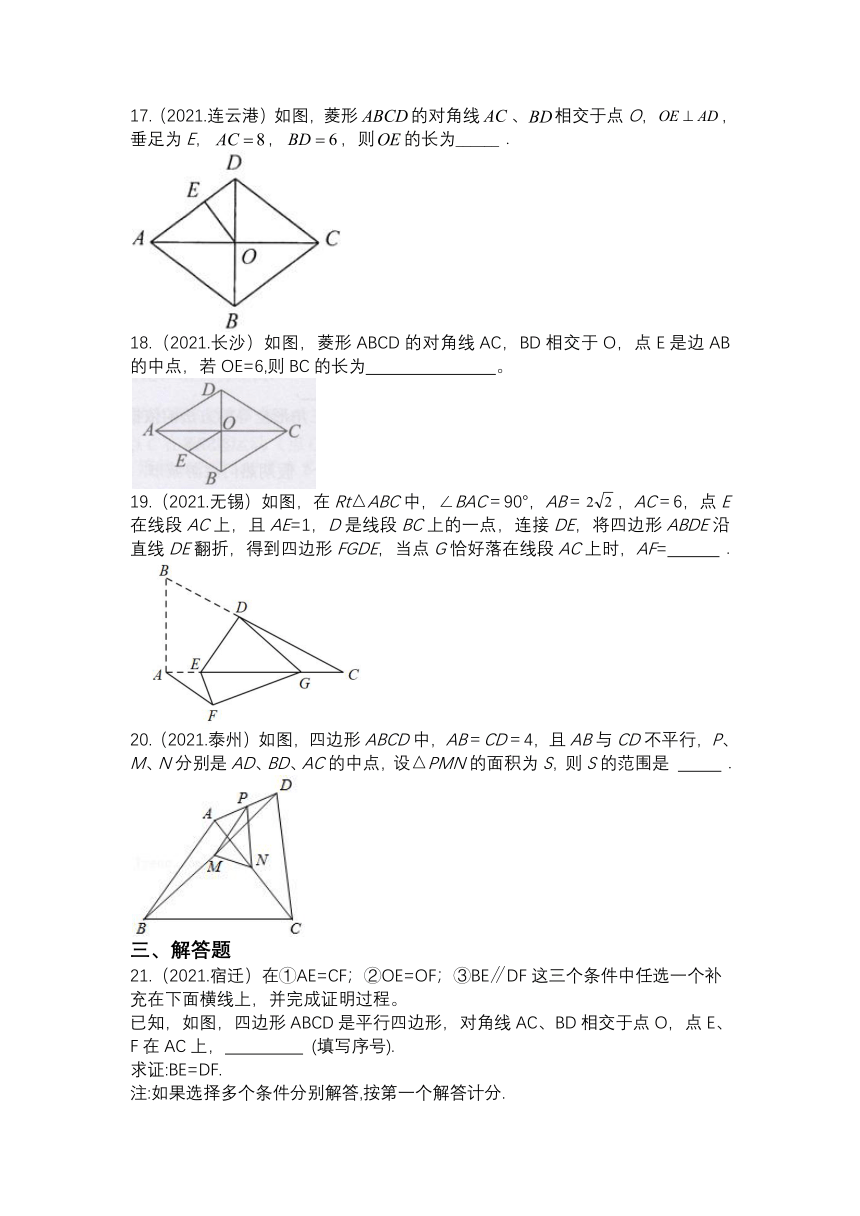
17.(2021.连云港)如图,菱形的对角线、相交于点O,,垂足为E,,,则的长为______.
18.(2021.长沙)如图,菱形ABCD的对角线AC,BD相交于O,点E是边AB的中点,若OE=6,则BC的长为 。
19.(2021.无锡)如图,在Rt△ABC中,∠BAC=90°,AB=,AC=6,点E在线段AC上,且AE=1,D是线段BC上的一点,连接DE,将四边形ABDE沿直线DE翻折,得到四边形FGDE,当点G恰好落在线段AC上时,AF= .
20.(2021.泰州)如图,四边形ABCD中,AB=CD=4,且AB与CD不平行,P、M、N分别是AD、BD、AC的中点,设△PMN的面积为S,则S的范围是 .
三、解答题
21.(2021.宿迁)在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程。
已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上, (填写序号).
求证:BE=DF.
注:如果选择多个条件分别解答,按第一个解答计分.
22.(2021.镇江)如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF。
(1)求证:△ABE≌△CDF;
(2)连接BD,∠1=30°,∠2=20°,当∠ABE= °时,四边形BFDE是菱形。
23.(2021.徐州)如图,将一张长方形纸片沿折叠,使两点重合.点落在点处.已知,.
(1)求证:是等腰三角形;
(2)求线段的长.
24.(2021.连云港)如图,点C是的中点,四边形是平行四边形.
(1)求证:四边形是平行四边形;
(2)如果,求证:四边形是矩形.
25.(2021.盐城)如图,D、E、F分别是△ABC各边的中点,连接DE、EF、AE.
(1)求证:四边形ADEF为平行四边形;
(2)加上条件 后,能使得四边形ADEF为菱形,请从①∠BAC=90°;②AE平分∠BAC;③AB=AC这三个条件中选择1个条件填空(写序号),并加以证明.
26.(2021.连云港)在数学兴趣小组活动中,小亮进行数学探究活动.
(1)是边长为3的等边三角形,E是边上的一点,且,小亮以为边作等边三角形,如图1,求的长;
(2)是边长为3的等边三角形,E是边上的一个动点,小亮以为边作等边三角形,如图2,在点E从点C到点A的运动过程中,求点F所经过的路径长;
(3)是边长为3的等边三角形,M是高上的一个动点,小亮以为边作等边三角形,如图3,在点M从点C到点D的运动过程中,求点N所经过的路径长;
(4)正方形的边长为3,E是边上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形,其中点F、G都在直线上,如图4,当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为______,点G所经过的路径长为______.
2021-2022学年苏科版八年级数学(下)第九单元《中心对称图形-平行四边形》2021年中考真题单元测试(答案)
一、选择题
1.(2021.徐州)下列图形,是轴对称图形但不是中心对称图形的是( )
A. B.
C. D.
【答案】D
2.(2021.苏州)如图,在平行四边形ABCD中,将△ABC沿着AC所在的直线得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是( )
A.1 B. C. D.
【答案】B
3.(2021.宿迁)如图,折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )
A. B.2 C. D.4
【答案】B
4.(2021.无锡)如图,D、E、F分别是△ABC各边中点,则以下说法错误的是( )
A.△BDE和△DCF的面积相等 B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形 D.若∠A=90°,则四边形AEDF是矩形
【答案】A
5.(2021.安徽)如图,在菱形ABCD中,,,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
【答案】A
6.(2021.青岛)如图,在四边形纸片ABCD中,AD∥BC,AB=10,∠B=60°,将纸片折叠,使点B落在AD边上的点G处,折痕为EF,若∠BFE=45°,则BF的长为( )
A.5 B.3 C.5 D.
【答案】C
7.(2021.成都)如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
【答案】C
8.(2021.遂宁)如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C恰好落在AB边上的F处,则CE的长是( )
A.1 B. C. D.
【答案】B
9.(2021.泰州).如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( )
A.2α B.90°﹣α C.45°+α D.90°﹣α
【答案】B
10.(2021.连云港)如图,将矩形纸片沿折叠后,点D、C分别落在点、的位置,的延长线交于点G,若,则等于( )
A. B. C. D.
【答案】A
11.(2021.丽水)如图,在Rt△ABC纸片中,∠ACB=90°,AC=4,BC=3,点D,E分别在AB,AC上,连结DE,将△ADE沿DE翻折,使点A的对应点F落在BC的延长线上,若FD平分∠EFB,则AD的长为( )
A. B. C. D.
【答案】D
12.(2021.重庆A)如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
【答案】C
二、填空题
13.(2021.徐州) 如图,四边形与均为矩形,点分别在线段上.若,矩形的周长为,则图中阴影部分的面积为___________.
【答案】16
14.(2021.扬州)如图,在 ABCD中,点E在AD上,且EC平分∠BED,若∠EBC=30°,BE=10,则 ABCD的面积为 .
【答案】50
15.(2021·苏州)如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为 .(结果保留根号)
【答案】2
16.(2021.盐城)如图,在矩形ABCD中,AB=3,AD=4,E、F分别是边BC、CD上一点,EF⊥AE,将△ECF沿EF翻折得△ECF,连接AC,当BE= 时,△AEC是以AE为腰的等腰三角形.
【答案】
17.(2021.连云港)如图,菱形的对角线、相交于点O,,垂足为E,,,则的长为______.
【答案】
18.(2021.长沙)如图,菱形ABCD的对角线AC,BD相交于O,点E是边AB的中点,若OE=6,则BC的长为 。
【答案】12
19.(2021.无锡)如图,在Rt△ABC中,∠BAC=90°,AB=,AC=6,点E在线段AC上,且AE=1,D是线段BC上的一点,连接DE,将四边形ABDE沿直线DE翻折,得到四边形FGDE,当点G恰好落在线段AC上时,AF= .
【答案】
20.(2021.泰州)如图,四边形ABCD中,AB=CD=4,且AB与CD不平行,P、M、N分别是AD、BD、AC的中点,设△PMN的面积为S,则S的范围是 .
【答案】0<S≤2
三、解答题
21.(2021.宿迁)在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上, (填写序号).
求证:BE=DF.
注:如果选择多个条件分别解答,按第一个解答计分.
解:选②,连接DE和BF
∵四边形ABCD是平行四边形
∴OB=OD
又∵OE=OF
∴四边形EDFB为平行四边形
22.(2021.镇江)如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF。
(1)求证:△ABE≌△CDF;
(2)连接BD,∠1=30°,∠2=20°,当∠ABE= °时,四边形BFDE是菱形。
解:(1)∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,AB=CD
∴∠EAB=∠ADC,∠ADC=∠DCF
∴∠EAB=∠DCF
在△ABE和△CDF中
AB=CD
∠EAB=∠DCF
AE=CF
∴△ABE≌△CDF(SAS)
(2)∠ABE=10°
23.(2021.徐州)如图,将一张长方形纸片沿折叠,使两点重合.点落在点处.已知,.
(1)求证:是等腰三角形;
(2)求线段的长.
解:(1)四边形是矩形
因为折叠,则
是等腰三角形
(2)四边形是矩形
,
设,则
因为折叠,则,,
在中
即
解得:
24.(2021.连云港)如图,点C是的中点,四边形是平行四边形.
(1)求证:四边形是平行四边形;
(2)如果,求证:四边形是矩形.
【答案】(1)见解析;(2)见解析
【解析】
【分析】(1)由平行四边形的性质以及点C是BE的中点,得到AD∥CE,AD=CE,从而证明四边形ACED是平行四边形;
(2)由平行四边形的性质证得DC=AE,从而证明平行四边形ACED是矩形.
【详解】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC.
∵点C是BE的中点,
∴BC=CE,
∴AD=CE,
∵AD∥CE,
∴四边形ACED是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AB=DC,
∵AB=AE,
∴DC=AE,
∵四边形ACED是平行四边形,
∴四边形ACED是矩形.
25.(2021.盐城)如图,D、E、F分别是△ABC各边的中点,连接DE、EF、AE.
(1)求证:四边形ADEF为平行四边形;
(2)加上条件 后,能使得四边形ADEF为菱形,请从①∠BAC=90°;②AE平分∠BAC;③AB=AC这三个条件中选择1个条件填空(写序号),并加以证明.
26.(2021.连云港)在数学兴趣小组活动中,小亮进行数学探究活动.
(1)是边长为3的等边三角形,E是边上的一点,且,小亮以为边作等边三角形,如图1,求的长;
(2)是边长为3的等边三角形,E是边上的一个动点,小亮以为边作等边三角形,如图2,在点E从点C到点A的运动过程中,求点F所经过的路径长;
(3)是边长为3的等边三角形,M是高上的一个动点,小亮以为边作等边三角形,如图3,在点M从点C到点D的运动过程中,求点N所经过的路径长;
(4)正方形的边长为3,E是边上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形,其中点F、G都在直线上,如图4,当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为______,点G所经过的路径长为______.
解:(1)∵、是等边三角形,
∴,,.
∴,
∴,
∴,
∴;
(2)连接,
∵、是等边三角形,
∴,,.
∴,
∴,
∴,
∴,,
∵,
∴,
∴,
又点在处时,,点在A处时,点与重合.
∴点运动的路径的长;
(3)取中点,连接,
∴,
∴,
∵,
∴,
∴,
∵、是等边三角形,
∴,,
∴,
∴,
∴,
∴,,
∴,
又点在处时,,点在处时,点与重合,
∴点所经过的路径的长。
一、选择题
1.(2021.徐州)下列图形,是轴对称图形但不是中心对称图形的是( )
A. B.
C. D.
2.(2021.苏州)如图,在平行四边形ABCD中,将△ABC沿着AC所在的直线得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是( )
A.1 B. C. D.
3.(2021.宿迁)如图,折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )
A. B.2 C. D.4
4.(2021.无锡)如图,D、E、F分别是△ABC各边中点,则以下说法错误的是( )
A.△BDE和△DCF的面积相等 B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形 D.若∠A=90°,则四边形AEDF是矩形
5.(2021.安徽)如图,在菱形ABCD中,,,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
6.(2021.青岛)如图,在四边形纸片ABCD中,AD∥BC,AB=10,∠B=60°,将纸片折叠,使点B落在AD边上的点G处,折痕为EF,若∠BFE=45°,则BF的长为( )
A.5 B.3 C.5 D.
7.(2021.成都)如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
8.(2021.遂宁)如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C恰好落在AB边上的F处,则CE的长是( )
A.1 B. C. D.
9.(2021.泰州).如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( )
A.2α B.90°﹣α C.45°+α D.90°﹣α
10.(2021.连云港)如图,将矩形纸片沿折叠后,点D、C分别落在点、的位置,的延长线交于点G,若,则等于( )
A. B. C. D.
11.(2021.丽水)如图,在Rt△ABC纸片中,∠ACB=90°,AC=4,BC=3,点D,E分别在AB,AC上,连结DE,将△ADE沿DE翻折,使点A的对应点F落在BC的延长线上,若FD平分∠EFB,则AD的长为( )
A. B. C. D.
12.(2021.重庆A)如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
二、填空题
13.(2021.徐州) 如图,四边形与均为矩形,点分别在线段上.若,矩形的周长为,则图中阴影部分的面积为___________.
14.(2021.扬州)如图,在 ABCD中,点E在AD上,且EC平分∠BED,若∠EBC=30°,BE=10,则 ABCD的面积为 .
15.(2021·苏州)如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为 .(结果保留根号)
16.(2021.盐城)如图,在矩形ABCD中,AB=3,AD=4,E、F分别是边BC、CD上一点,EF⊥AE,将△ECF沿EF翻折得△ECF,连接AC,当BE= 时,△AEC是以AE为腰的等腰三角形.
17.(2021.连云港)如图,菱形的对角线、相交于点O,,垂足为E,,,则的长为______.
18.(2021.长沙)如图,菱形ABCD的对角线AC,BD相交于O,点E是边AB的中点,若OE=6,则BC的长为 。
19.(2021.无锡)如图,在Rt△ABC中,∠BAC=90°,AB=,AC=6,点E在线段AC上,且AE=1,D是线段BC上的一点,连接DE,将四边形ABDE沿直线DE翻折,得到四边形FGDE,当点G恰好落在线段AC上时,AF= .
20.(2021.泰州)如图,四边形ABCD中,AB=CD=4,且AB与CD不平行,P、M、N分别是AD、BD、AC的中点,设△PMN的面积为S,则S的范围是 .
三、解答题
21.(2021.宿迁)在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程。
已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上, (填写序号).
求证:BE=DF.
注:如果选择多个条件分别解答,按第一个解答计分.
22.(2021.镇江)如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF。
(1)求证:△ABE≌△CDF;
(2)连接BD,∠1=30°,∠2=20°,当∠ABE= °时,四边形BFDE是菱形。
23.(2021.徐州)如图,将一张长方形纸片沿折叠,使两点重合.点落在点处.已知,.
(1)求证:是等腰三角形;
(2)求线段的长.
24.(2021.连云港)如图,点C是的中点,四边形是平行四边形.
(1)求证:四边形是平行四边形;
(2)如果,求证:四边形是矩形.
25.(2021.盐城)如图,D、E、F分别是△ABC各边的中点,连接DE、EF、AE.
(1)求证:四边形ADEF为平行四边形;
(2)加上条件 后,能使得四边形ADEF为菱形,请从①∠BAC=90°;②AE平分∠BAC;③AB=AC这三个条件中选择1个条件填空(写序号),并加以证明.
26.(2021.连云港)在数学兴趣小组活动中,小亮进行数学探究活动.
(1)是边长为3的等边三角形,E是边上的一点,且,小亮以为边作等边三角形,如图1,求的长;
(2)是边长为3的等边三角形,E是边上的一个动点,小亮以为边作等边三角形,如图2,在点E从点C到点A的运动过程中,求点F所经过的路径长;
(3)是边长为3的等边三角形,M是高上的一个动点,小亮以为边作等边三角形,如图3,在点M从点C到点D的运动过程中,求点N所经过的路径长;
(4)正方形的边长为3,E是边上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形,其中点F、G都在直线上,如图4,当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为______,点G所经过的路径长为______.
2021-2022学年苏科版八年级数学(下)第九单元《中心对称图形-平行四边形》2021年中考真题单元测试(答案)
一、选择题
1.(2021.徐州)下列图形,是轴对称图形但不是中心对称图形的是( )
A. B.
C. D.
【答案】D
2.(2021.苏州)如图,在平行四边形ABCD中,将△ABC沿着AC所在的直线得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是( )
A.1 B. C. D.
【答案】B
3.(2021.宿迁)如图,折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )
A. B.2 C. D.4
【答案】B
4.(2021.无锡)如图,D、E、F分别是△ABC各边中点,则以下说法错误的是( )
A.△BDE和△DCF的面积相等 B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形 D.若∠A=90°,则四边形AEDF是矩形
【答案】A
5.(2021.安徽)如图,在菱形ABCD中,,,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
【答案】A
6.(2021.青岛)如图,在四边形纸片ABCD中,AD∥BC,AB=10,∠B=60°,将纸片折叠,使点B落在AD边上的点G处,折痕为EF,若∠BFE=45°,则BF的长为( )
A.5 B.3 C.5 D.
【答案】C
7.(2021.成都)如图,四边形ABCD是菱形,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是( )
A.BE=DF B.∠BAE=∠DAF C.AE=AD D.∠AEB=∠AFD
【答案】C
8.(2021.遂宁)如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C恰好落在AB边上的F处,则CE的长是( )
A.1 B. C. D.
【答案】B
9.(2021.泰州).如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP为( )
A.2α B.90°﹣α C.45°+α D.90°﹣α
【答案】B
10.(2021.连云港)如图,将矩形纸片沿折叠后,点D、C分别落在点、的位置,的延长线交于点G,若,则等于( )
A. B. C. D.
【答案】A
11.(2021.丽水)如图,在Rt△ABC纸片中,∠ACB=90°,AC=4,BC=3,点D,E分别在AB,AC上,连结DE,将△ADE沿DE翻折,使点A的对应点F落在BC的延长线上,若FD平分∠EFB,则AD的长为( )
A. B. C. D.
【答案】D
12.(2021.重庆A)如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
【答案】C
二、填空题
13.(2021.徐州) 如图,四边形与均为矩形,点分别在线段上.若,矩形的周长为,则图中阴影部分的面积为___________.
【答案】16
14.(2021.扬州)如图,在 ABCD中,点E在AD上,且EC平分∠BED,若∠EBC=30°,BE=10,则 ABCD的面积为 .
【答案】50
15.(2021·苏州)如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F,若DF=,则对角线BD的长为 .(结果保留根号)
【答案】2
16.(2021.盐城)如图,在矩形ABCD中,AB=3,AD=4,E、F分别是边BC、CD上一点,EF⊥AE,将△ECF沿EF翻折得△ECF,连接AC,当BE= 时,△AEC是以AE为腰的等腰三角形.
【答案】
17.(2021.连云港)如图,菱形的对角线、相交于点O,,垂足为E,,,则的长为______.
【答案】
18.(2021.长沙)如图,菱形ABCD的对角线AC,BD相交于O,点E是边AB的中点,若OE=6,则BC的长为 。
【答案】12
19.(2021.无锡)如图,在Rt△ABC中,∠BAC=90°,AB=,AC=6,点E在线段AC上,且AE=1,D是线段BC上的一点,连接DE,将四边形ABDE沿直线DE翻折,得到四边形FGDE,当点G恰好落在线段AC上时,AF= .
【答案】
20.(2021.泰州)如图,四边形ABCD中,AB=CD=4,且AB与CD不平行,P、M、N分别是AD、BD、AC的中点,设△PMN的面积为S,则S的范围是 .
【答案】0<S≤2
三、解答题
21.(2021.宿迁)在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上, (填写序号).
求证:BE=DF.
注:如果选择多个条件分别解答,按第一个解答计分.
解:选②,连接DE和BF
∵四边形ABCD是平行四边形
∴OB=OD
又∵OE=OF
∴四边形EDFB为平行四边形
22.(2021.镇江)如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF。
(1)求证:△ABE≌△CDF;
(2)连接BD,∠1=30°,∠2=20°,当∠ABE= °时,四边形BFDE是菱形。
解:(1)∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,AB=CD
∴∠EAB=∠ADC,∠ADC=∠DCF
∴∠EAB=∠DCF
在△ABE和△CDF中
AB=CD
∠EAB=∠DCF
AE=CF
∴△ABE≌△CDF(SAS)
(2)∠ABE=10°
23.(2021.徐州)如图,将一张长方形纸片沿折叠,使两点重合.点落在点处.已知,.
(1)求证:是等腰三角形;
(2)求线段的长.
解:(1)四边形是矩形
因为折叠,则
是等腰三角形
(2)四边形是矩形
,
设,则
因为折叠,则,,
在中
即
解得:
24.(2021.连云港)如图,点C是的中点,四边形是平行四边形.
(1)求证:四边形是平行四边形;
(2)如果,求证:四边形是矩形.
【答案】(1)见解析;(2)见解析
【解析】
【分析】(1)由平行四边形的性质以及点C是BE的中点,得到AD∥CE,AD=CE,从而证明四边形ACED是平行四边形;
(2)由平行四边形的性质证得DC=AE,从而证明平行四边形ACED是矩形.
【详解】证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC.
∵点C是BE的中点,
∴BC=CE,
∴AD=CE,
∵AD∥CE,
∴四边形ACED是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AB=DC,
∵AB=AE,
∴DC=AE,
∵四边形ACED是平行四边形,
∴四边形ACED是矩形.
25.(2021.盐城)如图,D、E、F分别是△ABC各边的中点,连接DE、EF、AE.
(1)求证:四边形ADEF为平行四边形;
(2)加上条件 后,能使得四边形ADEF为菱形,请从①∠BAC=90°;②AE平分∠BAC;③AB=AC这三个条件中选择1个条件填空(写序号),并加以证明.
26.(2021.连云港)在数学兴趣小组活动中,小亮进行数学探究活动.
(1)是边长为3的等边三角形,E是边上的一点,且,小亮以为边作等边三角形,如图1,求的长;
(2)是边长为3的等边三角形,E是边上的一个动点,小亮以为边作等边三角形,如图2,在点E从点C到点A的运动过程中,求点F所经过的路径长;
(3)是边长为3的等边三角形,M是高上的一个动点,小亮以为边作等边三角形,如图3,在点M从点C到点D的运动过程中,求点N所经过的路径长;
(4)正方形的边长为3,E是边上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形,其中点F、G都在直线上,如图4,当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为______,点G所经过的路径长为______.
解:(1)∵、是等边三角形,
∴,,.
∴,
∴,
∴,
∴;
(2)连接,
∵、是等边三角形,
∴,,.
∴,
∴,
∴,
∴,,
∵,
∴,
∴,
又点在处时,,点在A处时,点与重合.
∴点运动的路径的长;
(3)取中点,连接,
∴,
∴,
∵,
∴,
∴,
∵、是等边三角形,
∴,,
∴,
∴,
∴,
∴,,
∴,
又点在处时,,点在处时,点与重合,
∴点所经过的路径的长。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
