2021—2022学年+人教版九年级数学下册27.2.2相似三角形的性质练习题(Word版含答案)
文档属性
| 名称 | 2021—2022学年+人教版九年级数学下册27.2.2相似三角形的性质练习题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 280.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 10:23:16 | ||
图片预览

文档简介
2021——2022学年度人教版九年级数学下册 第二十七章 相似 27.2.2 相似三角形的性质 练习题
一、选择题
1.如果一个三角形保持形状不变,但周长扩大为原来的倍,那么这个三角形的边长扩大为原来的( )
A.2倍 B.4倍 C.8倍 D.16倍
2.如图,在2×3的方格中,画有格点△ABC,下列选项的方格中所画格点三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
3.两个相似多边形的相似比是3:4,其中小多边形的面积为18cm2,则较大多边形的面积为( )
A.16cm2 B.54cm2 C.32cm2 D.48cm2
4.如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,则S△AOB:S△DOC=( )
A.2:3 B.9:25 C.4:9 D.9:4
5.如图,已知△ABC∽△DEF,若∠A=35°,∠B=65°,则∠F的度数是( )
A.30° B.35° C.80° D.100°
6.如图,∠BEC=∠CDB,下列结论正确的是( )
A.EF BF=DF CF B.BE CD=BF CF
C.AE AB=AD AC D.AE BE=AD DC
7.如图所示,在中,,,于,是线段上一个动点,以为直角顶点向下作等腰,连结,,则的最小值为( )
A. B. C. D.
8.如图,在菱形ABCD中,点F在线段CD上,连接EF,且∠CBE+∠EFC=180°,DF=2,FC=3.则DB=( )
A.6 B. C.5 D.
9.如图,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( )cm.
A. B.5 C. D.8
10.如图,已知点A(0,1),B(﹣3,0),连接AB,将△ABO沿AB翻折,使点O与点C重合,且点C恰好在函数y=上,则k的值为( )
A. B. C. D.
二、填空题
11.若两个相似多边形的面积之比为1:4.周长之差为6,则这两个相似多边形的周长分别是________.
12.如图,AB,CD相交于O点,△AOC∽△BOD,OC:CD=1:3,AC=2,则BD的长为 __.
13.如图,中,,,,点是边上一点,将沿经过点的直线折叠,使得点落在边上的处,若恰好和相似,则此时的长为______.
14.如图,在平行四边形ABCD中,E是AB的延长线上的一点,DE与边BC相交于点F,,那么的值为________________.
15.已知如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△CPE:S△ABC=_____.
三、解答题
16.如图,在中,是边上的一点,若,求证:.
17.如图所示,已知△AOB∽△DOC,OA=2,AD=9,OB=5,DC=12,∠A=58°,求AB、OC的长和∠D的度数.
18.如图,点D、E分别是△ABC的边AC、AB上的点,且∠ADE=∠B,其中AE=1.5,AC=2,BC=3,求DE的长.
19.如图所示,D,E分别是AB,AC上的点,△ADE∽△ABC,相似比是,DE=4cm,∠C=30°,求BC,∠AED.
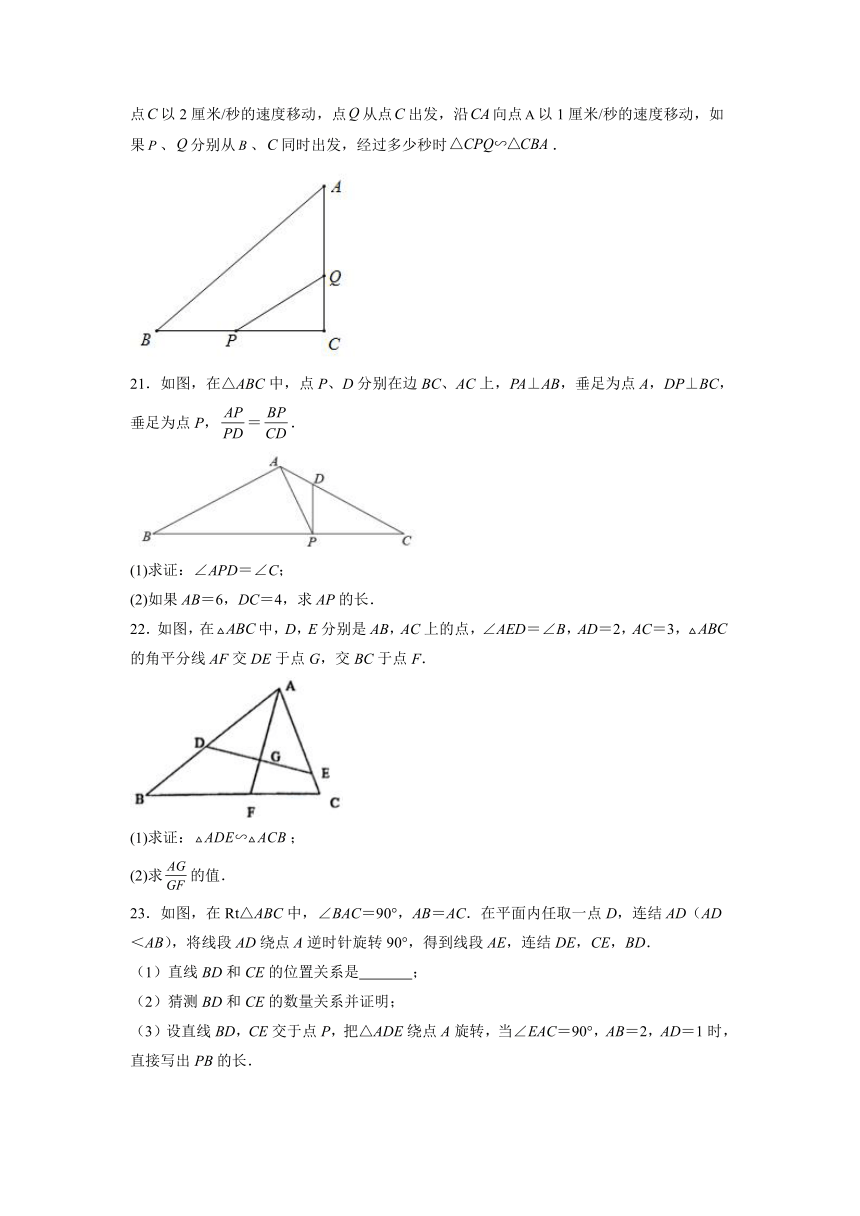
20.已知如图中,,,,点从点出发,沿向点以2厘米/秒的速度移动,点从点出发,沿向点以1厘米/秒的速度移动,如果、分别从、同时出发,经过多少秒时.
21.如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P,=.
(1)求证:∠APD=∠C;
(2)如果AB=6,DC=4,求AP的长.
22.如图,在中,D,E分别是AB,AC上的点,∠AED=∠B,AD=2,AC=3,的角平分线AF交DE于点G,交BC于点F.
(1)求证:;
(2)求的值.
23.如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)直线BD和CE的位置关系是 ;
(2)猜测BD和CE的数量关系并证明;
(3)设直线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,直接写出PB的长.
【参考答案】
1.B 2.A 3.C 4.C 5.C 6.C 7.B 8.D 9.C 10.B
11.6, 12
12.4
13.或.
14.
15.1:8.
16.证明:∵,
∴,
∴,
即.
17.解:∵OA=2,AD=9,
∴OD=9﹣2=7,
∵AB∥CD,
∴△AOB∽△DOC,
∴==,
∵OA=2,OB=5,DC=12,
∴==,
解得OC=,AB=,
∵△AOB∽△DOC,
∴∠D=∠A=58°.
18.解:∵∠A=∠A,且已知∠ADE=∠B,
∴△ADE∽△ABC,
∴,代入数据AE=1.5,AC=2,BC=3,
∴,
解得:DE=,
故DE的长为.
19.∵△ADE∽△ABC,
∴∠AED=∠C=30°,,
∵DE=4cm,
∴BC=10cm.
20.解:∵,
∴
∴设经过秒后,则,,
∴
∴
∴如果、分别从、同时出发,经过时.
21(1)证明:∵PA⊥AB,DP⊥BC,
∴∠BAP=∠DPC=90°,
设==k,
∴AP=k PD,BP=k CD,
∴AB=,PC=,
∴=k==,
∴Rt△ABP∽Rt△PCD,
∴∠B=∠C,∠APB=∠CDP,
∵∠DPB=∠C+∠CDP=∠APB+∠APD,
∴∠APD=∠C;
(2)解:∵∠B=∠C,
∴AB=AC=6,
∵CD=4,
∴AD=2,
∵∠APD=∠C,∠CAP=∠PAD,
∴△APC∽△ADP,
∴,
∴AP2=2×6=12,
∴AP=2.
(1)证明:∵∠AED=∠B,∠BAC=∠DAE,
∴△ADE∽△ACB;
(2)解:∵△ADE∽△ACB,
∴∠ADE=∠C,
∵AF平分∠BAC,
∴∠DAG=∠CAF,
∴△ADG∽△ACF,
∴ ,
∵AD=2,AC=3,
∴,
∴=2.
23.解:(1)BD⊥CE,
理由:延长CE交BD于P,
∵将线段AD绕点A逆时针旋转90°,得到线段AE,
∴AD=AE,∠DAE=90°,
∵∠BAC=90°,AB=AC,
∵∠DAB+∠BAE=∠CAE+∠BAE=90°,
∴∠DAB=∠EAC,
∴△DAB≌△EAC(SAS),
∴∠ABD=∠ACE,
∵∠ABC+∠ACB=∠ABP+∠ABC+∠PCB=90°,
∴∠BPC=90°,
∴BD⊥CE,
故答案为:BD⊥CE;
(2)BD和CE的数量是:BD=CE;
由(1)知△ABD≌△ACE,
∴BD=CE;
(3)①当点E在AB上时,BE=AB﹣AE=1.
∵∠EAC=90°,
∴CE==,
同(1)可证△ADB≌△AEC.
∵∠AEC=∠BEP,
∴∠BPE=∠EAC=90°,
∵∠PBE=∠ABD,
∴△BPE∽△BAD,
∴=,
∴=,
∴BP=.
②当点E在BA延长线上时,BE=3,
∵∠EAC=90°,
∴CE==,
由△BPE∽△BAD,
∴=,
∴=,
∴PB=,
综上所述,PB的长为或.
一、选择题
1.如果一个三角形保持形状不变,但周长扩大为原来的倍,那么这个三角形的边长扩大为原来的( )
A.2倍 B.4倍 C.8倍 D.16倍
2.如图,在2×3的方格中,画有格点△ABC,下列选项的方格中所画格点三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
3.两个相似多边形的相似比是3:4,其中小多边形的面积为18cm2,则较大多边形的面积为( )
A.16cm2 B.54cm2 C.32cm2 D.48cm2
4.如图,AB∥CD,AD与BC交于点O,AD:OD=5:3,则S△AOB:S△DOC=( )
A.2:3 B.9:25 C.4:9 D.9:4
5.如图,已知△ABC∽△DEF,若∠A=35°,∠B=65°,则∠F的度数是( )
A.30° B.35° C.80° D.100°
6.如图,∠BEC=∠CDB,下列结论正确的是( )
A.EF BF=DF CF B.BE CD=BF CF
C.AE AB=AD AC D.AE BE=AD DC
7.如图所示,在中,,,于,是线段上一个动点,以为直角顶点向下作等腰,连结,,则的最小值为( )
A. B. C. D.
8.如图,在菱形ABCD中,点F在线段CD上,连接EF,且∠CBE+∠EFC=180°,DF=2,FC=3.则DB=( )
A.6 B. C.5 D.
9.如图,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( )cm.
A. B.5 C. D.8
10.如图,已知点A(0,1),B(﹣3,0),连接AB,将△ABO沿AB翻折,使点O与点C重合,且点C恰好在函数y=上,则k的值为( )
A. B. C. D.
二、填空题
11.若两个相似多边形的面积之比为1:4.周长之差为6,则这两个相似多边形的周长分别是________.
12.如图,AB,CD相交于O点,△AOC∽△BOD,OC:CD=1:3,AC=2,则BD的长为 __.
13.如图,中,,,,点是边上一点,将沿经过点的直线折叠,使得点落在边上的处,若恰好和相似,则此时的长为______.
14.如图,在平行四边形ABCD中,E是AB的延长线上的一点,DE与边BC相交于点F,,那么的值为________________.
15.已知如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△CPE:S△ABC=_____.
三、解答题
16.如图,在中,是边上的一点,若,求证:.
17.如图所示,已知△AOB∽△DOC,OA=2,AD=9,OB=5,DC=12,∠A=58°,求AB、OC的长和∠D的度数.
18.如图,点D、E分别是△ABC的边AC、AB上的点,且∠ADE=∠B,其中AE=1.5,AC=2,BC=3,求DE的长.
19.如图所示,D,E分别是AB,AC上的点,△ADE∽△ABC,相似比是,DE=4cm,∠C=30°,求BC,∠AED.
20.已知如图中,,,,点从点出发,沿向点以2厘米/秒的速度移动,点从点出发,沿向点以1厘米/秒的速度移动,如果、分别从、同时出发,经过多少秒时.
21.如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P,=.
(1)求证:∠APD=∠C;
(2)如果AB=6,DC=4,求AP的长.
22.如图,在中,D,E分别是AB,AC上的点,∠AED=∠B,AD=2,AC=3,的角平分线AF交DE于点G,交BC于点F.
(1)求证:;
(2)求的值.
23.如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)直线BD和CE的位置关系是 ;
(2)猜测BD和CE的数量关系并证明;
(3)设直线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,直接写出PB的长.
【参考答案】
1.B 2.A 3.C 4.C 5.C 6.C 7.B 8.D 9.C 10.B
11.6, 12
12.4
13.或.
14.
15.1:8.
16.证明:∵,
∴,
∴,
即.
17.解:∵OA=2,AD=9,
∴OD=9﹣2=7,
∵AB∥CD,
∴△AOB∽△DOC,
∴==,
∵OA=2,OB=5,DC=12,
∴==,
解得OC=,AB=,
∵△AOB∽△DOC,
∴∠D=∠A=58°.
18.解:∵∠A=∠A,且已知∠ADE=∠B,
∴△ADE∽△ABC,
∴,代入数据AE=1.5,AC=2,BC=3,
∴,
解得:DE=,
故DE的长为.
19.∵△ADE∽△ABC,
∴∠AED=∠C=30°,,
∵DE=4cm,
∴BC=10cm.
20.解:∵,
∴
∴设经过秒后,则,,
∴
∴
∴如果、分别从、同时出发,经过时.
21(1)证明:∵PA⊥AB,DP⊥BC,
∴∠BAP=∠DPC=90°,
设==k,
∴AP=k PD,BP=k CD,
∴AB=,PC=,
∴=k==,
∴Rt△ABP∽Rt△PCD,
∴∠B=∠C,∠APB=∠CDP,
∵∠DPB=∠C+∠CDP=∠APB+∠APD,
∴∠APD=∠C;
(2)解:∵∠B=∠C,
∴AB=AC=6,
∵CD=4,
∴AD=2,
∵∠APD=∠C,∠CAP=∠PAD,
∴△APC∽△ADP,
∴,
∴AP2=2×6=12,
∴AP=2.
(1)证明:∵∠AED=∠B,∠BAC=∠DAE,
∴△ADE∽△ACB;
(2)解:∵△ADE∽△ACB,
∴∠ADE=∠C,
∵AF平分∠BAC,
∴∠DAG=∠CAF,
∴△ADG∽△ACF,
∴ ,
∵AD=2,AC=3,
∴,
∴=2.
23.解:(1)BD⊥CE,
理由:延长CE交BD于P,
∵将线段AD绕点A逆时针旋转90°,得到线段AE,
∴AD=AE,∠DAE=90°,
∵∠BAC=90°,AB=AC,
∵∠DAB+∠BAE=∠CAE+∠BAE=90°,
∴∠DAB=∠EAC,
∴△DAB≌△EAC(SAS),
∴∠ABD=∠ACE,
∵∠ABC+∠ACB=∠ABP+∠ABC+∠PCB=90°,
∴∠BPC=90°,
∴BD⊥CE,
故答案为:BD⊥CE;
(2)BD和CE的数量是:BD=CE;
由(1)知△ABD≌△ACE,
∴BD=CE;
(3)①当点E在AB上时,BE=AB﹣AE=1.
∵∠EAC=90°,
∴CE==,
同(1)可证△ADB≌△AEC.
∵∠AEC=∠BEP,
∴∠BPE=∠EAC=90°,
∵∠PBE=∠ABD,
∴△BPE∽△BAD,
∴=,
∴=,
∴BP=.
②当点E在BA延长线上时,BE=3,
∵∠EAC=90°,
∴CE==,
由△BPE∽△BAD,
∴=,
∴=,
∴PB=,
综上所述,PB的长为或.
