2021—2022学年人教版九年级数学下册27.2.3相似三角形应用举例练习题 (Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册27.2.3相似三角形应用举例练习题 (Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 282.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 10:23:52 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学下册 第二十七章 相似
27.2.3 相似三角形应用举例 练习题
一、选择题
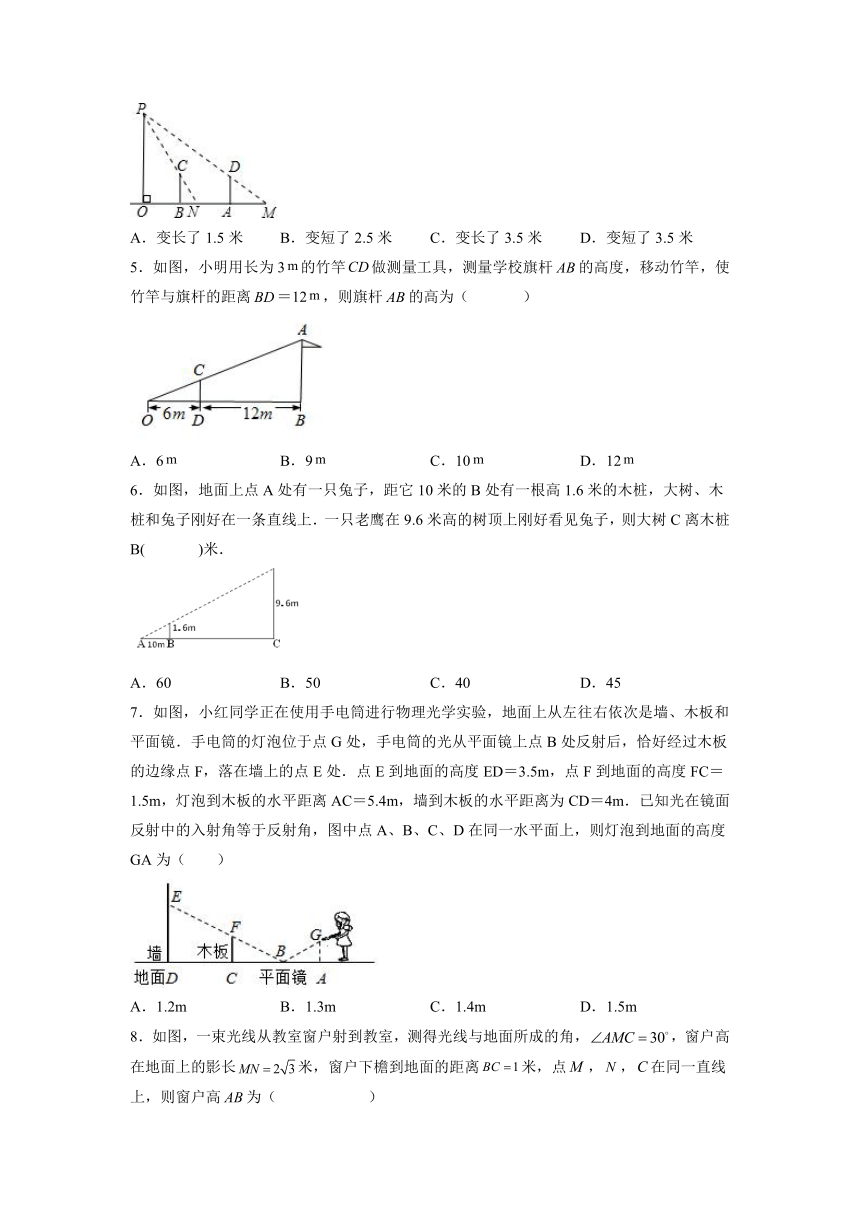
1.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,那么该古城墙CD的高度是( )
A.8m B.9m C.16m D.18m
2.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中①号“E”字的高度BC长为b,当测试距离为3m时,②号“E”字的高度DF长为( )
A.5b B.3b C.b D.b
3.一块直角三角形木板,它的一条直角边长为,面积为,甲、乙两人分别按图①、②把它加工成一个正方形桌面,则①、②中正方形的面积较大的是
A.① B.② C.一样大 D.无法判断
4.如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( )
A.变长了1.5米 B.变短了2.5米 C.变长了3.5米 D.变短了3.5米
5.如图,小明用长为3的竹竿做测量工具,测量学校旗杆的高度,移动竹竿,使竹竿与旗杆的距离=12,则旗杆的高为( )
A.6 B.9 C.10 D.12
6.如图,地面上点A处有一只兔子,距它10米的B处有一根高1.6米的木桩,大树、木桩和兔子刚好在一条直线上.一只老鹰在9.6米高的树顶上刚好看见兔子,则大树C离木桩B( )米.
A.60 B.50 C.40 D.45
7.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
A.1.2m B.1.3m C.1.4m D.1.5m
8.如图,一束光线从教室窗户射到教室,测得光线与地面所成的角,,窗户高在地面上的影长米,窗户下檐到地面的距离米,点,,在同一直线上,则窗户高为( )
A.米 B.米 C.米 D.米
9.如图所示,在离某建筑物4m处有一棵树,在某时刻,长的竹竿垂直地面,影长为2m,此时,树的影子有一部分映在地面上,还有一部分影子映在建筑物的墙上,墙上的影高为2m,则这棵树高约有多少米
A.米 B.米 C.米 D.米
10.如图一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )
A.8米 B.6米 C.4.5米 D.3米
二、填空题
11.小明的身高为1.7米,某一时刻小明的影长为1米,同一时刻测得小明身旁一棵树的影长为7米,则这棵树的高为___米.
12.如图,为了测量一栋楼的高度,王青同学在她脚下放了一面镜子,然后向后退,直到她刚好在镜子中看到大楼顶部.如果王青眼睛与地面的距离,同时量得,,则楼高______.
13.如图,一斜坡AB长80m,高BC为8m,将重物从坡底A推到坡上20m的M出处停下,则停止地点M的高度为__m.
14.如图,光源在水平横杆的上方,照射横杆得到它在平地上的影子为(点、、在一条直线上,点、、在一条直线上),不难发现.已知,,点到横杆的距离是,则点到地面的距离等于______.
15.如图,C,D分别是反比例函数图象上的点,且CD∥x轴,过C,D两点分别作x轴的垂线段,垂足分别为B,A两点,连接OC,交DA于点E,若,则k的值为___.
三、解答题
16.碧桂园进驻揭西,一栋栋高楼拔地而起.如图,小明(线段AB)利用学到的知识,计算楼房(线段CD)的层数,他把一镜子放在E处(点B、E、D共线),此时小明通过镜子刚好可以看到大楼的顶端C,若小明身高1.5m,测得BE=1m,ED=58m,碧桂园层高为2.9m,求这栋楼房有多少层?
17.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上).
18.学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑AB的高度(如图1).如图2,在地面BC上取E,G两点,分别竖立两根高为2m的标杆EF和GH,两标杆间隔EG为23m,并且古建筑AB,标杆EF和GH在同一竖直平面内,从标杆EF后退2m到D处,从D处观察A点,A,F,D三点成一线;从标杆GH后退4m到C处,从C处观察A点,A,H,C三点也成一线.请根据以上测量数据,帮助实践小组求出该古建筑的高度.
19.如图,中,,,,如果动点D以每秒2个单位长度的速度,从点B出发沿边BA向点A运动,此时直线,交AC于点E.记x秒时DE的长度为y,写出y关于x的函数解析式,并画出它的图象.
20.数学小组想利用所学知识测量一棵树的高度.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树梢影子末端重合于点H,测得米.随后,组员在直线上平放一平面镜,在镜面上做了一个标记,这个标记在直线上的对应位置为点G.镜子不动,小莉从点D沿着直线后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时米.如图,已知,,,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度.
21.同一时刻两根木杆在太阳光下的影子如图所示,木杆AB长为3m,其影子BC长1.6m,木杆QP长为4.8m,它的部分影子PM长为2m,还有一部分落到墙上的MN处,求墙上影子MN的长度.
22.如图:AB为路灯主杆,AE为路灯的悬臂,AE长3米,CD是长为1.8米的标杆.已知路灯悬臂AE与地面BG平行,当标杆竖立于地面时,主杆顶端A、标杆顶端D和地面上一点G在同一直线上,此时路灯E、标杆顶端D和地面上另一点F也在同一条直线上(路灯主杆底端B、标杆底端C和地面上点F、点G在同一水平线上).这时测得FG长1.5米,求路灯主杆AB的高度.
23.真身宝塔,位于陕西省扶风法门镇法门寺内,因塔下藏有佛祖真身舍利而得名.小玲和晓静很想知道真身宝塔的高度.于是,有一天,他们带着标杆和皮尺来到法门寺进行测量,测量方案如下:如图,首先,小玲在处放置一平面镜,她从点沿后退,当退行1.8米到处时,恰好在镜子中看到塔顶的像,此时测得小玲眼睛到地面的距离为1.5米;然后,晓静在处竖立了一根高1.6米的标杆,发现地面上的点、标杆顶点和塔顶在一条直线上,此时测得为2.4米,为11.7米.已知,,,点、、、、在一条直线上,请根据以上所测数据,计算真身宝塔的高度.
【参考答案】
1.A 2.C 3.A 4.D 5.B 6.B 7.A 8.A 9.C 10.C
11.11.9
12.20
13.2
14.3
15.3
16.30层
17.步
18.该古建筑的高度为25m.
19.,,图略
20.
21.1.05m
22.路灯主杆的高度为5.4米.
23.47
27.2.3 相似三角形应用举例 练习题
一、选择题
1.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,那么该古城墙CD的高度是( )
A.8m B.9m C.16m D.18m
2.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中①号“E”字的高度BC长为b,当测试距离为3m时,②号“E”字的高度DF长为( )
A.5b B.3b C.b D.b
3.一块直角三角形木板,它的一条直角边长为,面积为,甲、乙两人分别按图①、②把它加工成一个正方形桌面,则①、②中正方形的面积较大的是
A.① B.② C.一样大 D.无法判断
4.如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( )
A.变长了1.5米 B.变短了2.5米 C.变长了3.5米 D.变短了3.5米
5.如图,小明用长为3的竹竿做测量工具,测量学校旗杆的高度,移动竹竿,使竹竿与旗杆的距离=12,则旗杆的高为( )
A.6 B.9 C.10 D.12
6.如图,地面上点A处有一只兔子,距它10米的B处有一根高1.6米的木桩,大树、木桩和兔子刚好在一条直线上.一只老鹰在9.6米高的树顶上刚好看见兔子,则大树C离木桩B( )米.
A.60 B.50 C.40 D.45
7.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
A.1.2m B.1.3m C.1.4m D.1.5m
8.如图,一束光线从教室窗户射到教室,测得光线与地面所成的角,,窗户高在地面上的影长米,窗户下檐到地面的距离米,点,,在同一直线上,则窗户高为( )
A.米 B.米 C.米 D.米
9.如图所示,在离某建筑物4m处有一棵树,在某时刻,长的竹竿垂直地面,影长为2m,此时,树的影子有一部分映在地面上,还有一部分影子映在建筑物的墙上,墙上的影高为2m,则这棵树高约有多少米
A.米 B.米 C.米 D.米
10.如图一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )
A.8米 B.6米 C.4.5米 D.3米
二、填空题
11.小明的身高为1.7米,某一时刻小明的影长为1米,同一时刻测得小明身旁一棵树的影长为7米,则这棵树的高为___米.
12.如图,为了测量一栋楼的高度,王青同学在她脚下放了一面镜子,然后向后退,直到她刚好在镜子中看到大楼顶部.如果王青眼睛与地面的距离,同时量得,,则楼高______.
13.如图,一斜坡AB长80m,高BC为8m,将重物从坡底A推到坡上20m的M出处停下,则停止地点M的高度为__m.
14.如图,光源在水平横杆的上方,照射横杆得到它在平地上的影子为(点、、在一条直线上,点、、在一条直线上),不难发现.已知,,点到横杆的距离是,则点到地面的距离等于______.
15.如图,C,D分别是反比例函数图象上的点,且CD∥x轴,过C,D两点分别作x轴的垂线段,垂足分别为B,A两点,连接OC,交DA于点E,若,则k的值为___.
三、解答题
16.碧桂园进驻揭西,一栋栋高楼拔地而起.如图,小明(线段AB)利用学到的知识,计算楼房(线段CD)的层数,他把一镜子放在E处(点B、E、D共线),此时小明通过镜子刚好可以看到大楼的顶端C,若小明身高1.5m,测得BE=1m,ED=58m,碧桂园层高为2.9m,求这栋楼房有多少层?
17.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上).
18.学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑AB的高度(如图1).如图2,在地面BC上取E,G两点,分别竖立两根高为2m的标杆EF和GH,两标杆间隔EG为23m,并且古建筑AB,标杆EF和GH在同一竖直平面内,从标杆EF后退2m到D处,从D处观察A点,A,F,D三点成一线;从标杆GH后退4m到C处,从C处观察A点,A,H,C三点也成一线.请根据以上测量数据,帮助实践小组求出该古建筑的高度.
19.如图,中,,,,如果动点D以每秒2个单位长度的速度,从点B出发沿边BA向点A运动,此时直线,交AC于点E.记x秒时DE的长度为y,写出y关于x的函数解析式,并画出它的图象.
20.数学小组想利用所学知识测量一棵树的高度.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树梢影子末端重合于点H,测得米.随后,组员在直线上平放一平面镜,在镜面上做了一个标记,这个标记在直线上的对应位置为点G.镜子不动,小莉从点D沿着直线后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时米.如图,已知,,,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度.
21.同一时刻两根木杆在太阳光下的影子如图所示,木杆AB长为3m,其影子BC长1.6m,木杆QP长为4.8m,它的部分影子PM长为2m,还有一部分落到墙上的MN处,求墙上影子MN的长度.
22.如图:AB为路灯主杆,AE为路灯的悬臂,AE长3米,CD是长为1.8米的标杆.已知路灯悬臂AE与地面BG平行,当标杆竖立于地面时,主杆顶端A、标杆顶端D和地面上一点G在同一直线上,此时路灯E、标杆顶端D和地面上另一点F也在同一条直线上(路灯主杆底端B、标杆底端C和地面上点F、点G在同一水平线上).这时测得FG长1.5米,求路灯主杆AB的高度.
23.真身宝塔,位于陕西省扶风法门镇法门寺内,因塔下藏有佛祖真身舍利而得名.小玲和晓静很想知道真身宝塔的高度.于是,有一天,他们带着标杆和皮尺来到法门寺进行测量,测量方案如下:如图,首先,小玲在处放置一平面镜,她从点沿后退,当退行1.8米到处时,恰好在镜子中看到塔顶的像,此时测得小玲眼睛到地面的距离为1.5米;然后,晓静在处竖立了一根高1.6米的标杆,发现地面上的点、标杆顶点和塔顶在一条直线上,此时测得为2.4米,为11.7米.已知,,,点、、、、在一条直线上,请根据以上所测数据,计算真身宝塔的高度.
【参考答案】
1.A 2.C 3.A 4.D 5.B 6.B 7.A 8.A 9.C 10.C
11.11.9
12.20
13.2
14.3
15.3
16.30层
17.步
18.该古建筑的高度为25m.
19.,,图略
20.
21.1.05m
22.路灯主杆的高度为5.4米.
23.47
