2021-2022学年高一下学期数学北师大版(2019)必修第二册5.1正弦函数的图像与性质再认识(2)课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册5.1正弦函数的图像与性质再认识(2)课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 570.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
正弦函数的图像与性质再认识(2)
一、导入
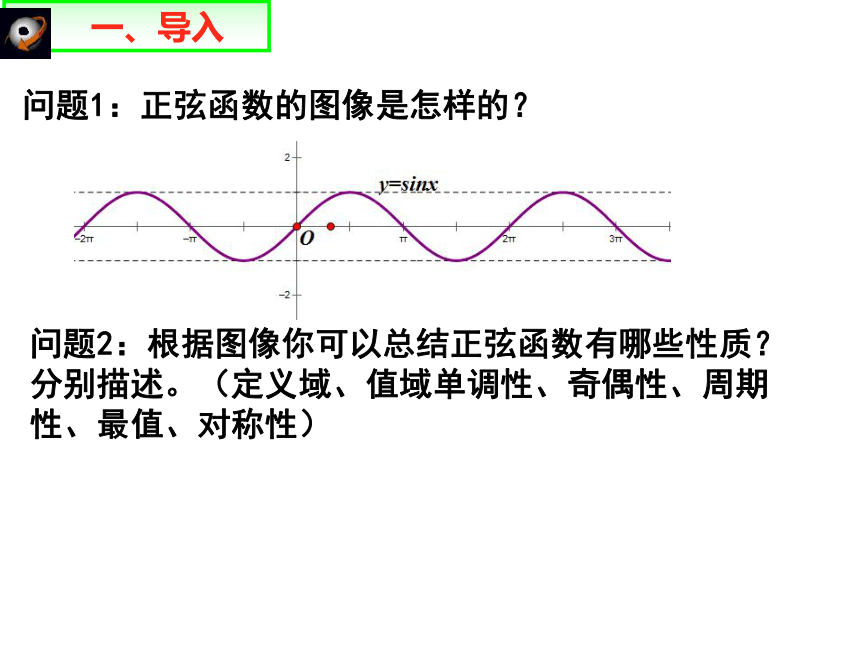
问题1:正弦函数的图像是怎样的?
问题2:根据图像你可以总结正弦函数有哪些性质?分别描述。(定义域、值域单调性、奇偶性、周期性、最值、对称性)
二、新授内容
正弦函数 y=sinx的定义域为R
1.定义域
2.值域
从正弦函数的图像可以看出,正弦曲线夹在两条平行线y=1和y=-1之间,所以值域为[-1,1]
当x∈A时,函数取得最大值1,反之,若函数取得最大值1时,x∈A.
当x∈B时,函数取得最小值-1,反之,若函数取得最小值-1时,x∈B.
二、新授内容
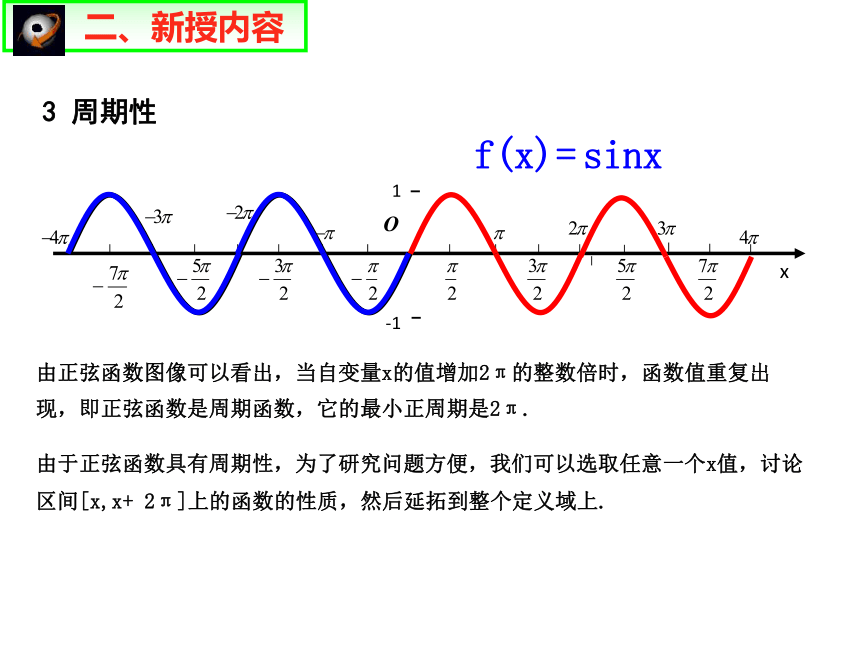
由正弦函数图像可以看出,当自变量x的值增加2π的整数倍时,函数值重复出现,即正弦函数是周期函数,它的最小正周期是2π.
3 周期性
由于正弦函数具有周期性,为了研究问题方便,我们可以选取任意一个x值,讨论区间[x,x+ 2π]上的函数的性质,然后延拓到整个定义域上.
x
1
-1
O
二、新授内容
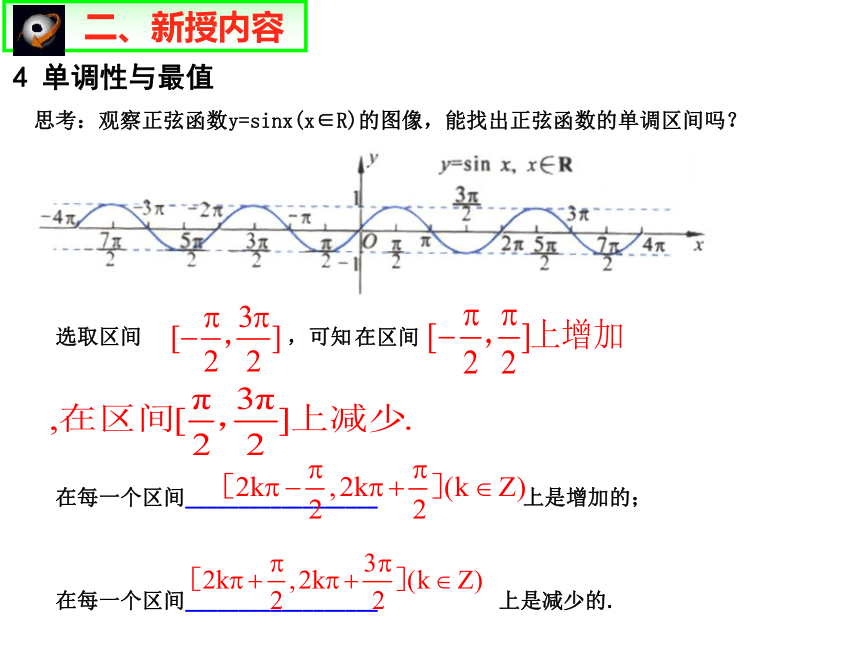
思考:观察正弦函数y=sinx(x∈R)的图像,能找出正弦函数的单调区间吗?
4 单调性与最值
选取区间 ,可知
在区间
在每一个区间__________________ 上是增加的;
在每一个区间__________________ 上是减少的.
二、新授内容
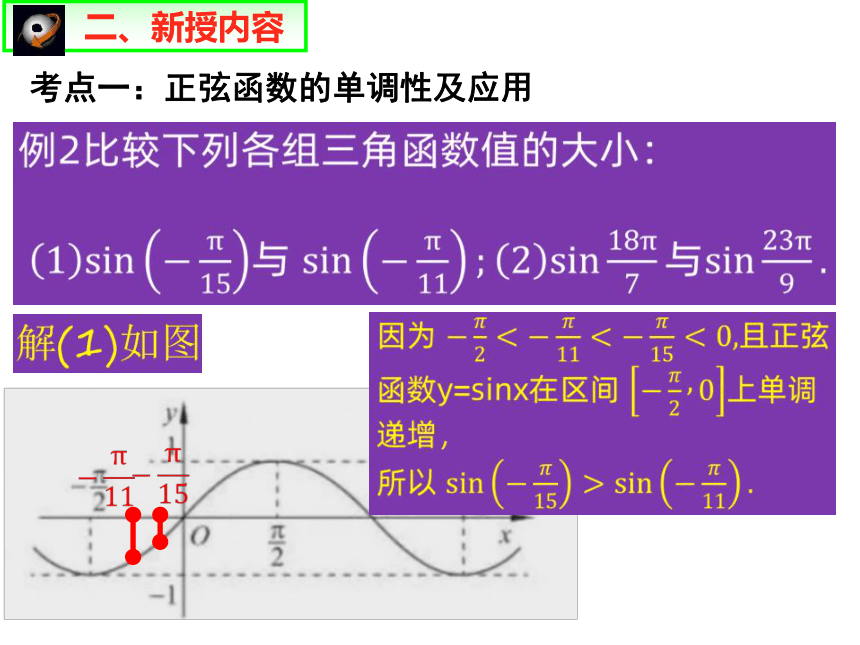
考点一:正弦函数的单调性及应用
探究问题:正弦函数的单调性是怎样的?
二、新授内容
考点一:正弦函数的单调性及应用
二、新授内容
考点一:正弦函数的单调性及应用
二、新授内容
考点一:正弦函数的单调性及应用
利用正弦函数单调性比较大小的步骤
(1)一定:利用诱导公式把角化到同一单调区间上.
(2)二比较:利用函数的单调性比较大小.
二、新授内容
考点一:正弦函数的单调性及应用
二、新授内容
x
y
1
-1
O
5 奇偶性
图像关于原点对称,奇函数关于原点对称.
根据诱导公式sin(-x)=sin x,可知正弦函数是奇函数
观察正弦函数的图像,可以看到
二、新授内容
6 对称性
二、新授内容
例2.画出函数y=sinx-1的图象,并讨论它的性质.
解:
函数 y=sinx-1 定义域 R 值域 [-2,0] 奇偶性 既不是奇函数,也不是偶函数 周期性 周期函数,周期是2π 单调性 在每一个闭区间 在每一个闭区间 都单调递增;
都单调递减
最大值与最小值 当 时,最大值为0; 当 时,最小值为-2 二、新授内容
考点二:正弦函数的奇偶性与周期性
二、新授内容
考点三:正弦函数的定义域与值域的应用
1:提炼知识点:
正弦函数的最值与值域
2:结合试题情境解题:
问题1:复合函数的值域怎么求?
问题2:函数y=sinx的值域是多少?
问题3:函数y何时取得最小值,何时取得最大值?
二、新授内容
【思路点拨】
考点三:图像的应用
三、反思归纳
(1)正弦函数的图像是怎样的?
(2)根据图像可以判断出正弦函数的定义域、值域、单调性、奇偶性、周期性以及对称性吗?
正弦函数的图像与性质再认识(2)
一、导入
问题1:正弦函数的图像是怎样的?
问题2:根据图像你可以总结正弦函数有哪些性质?分别描述。(定义域、值域单调性、奇偶性、周期性、最值、对称性)
二、新授内容
正弦函数 y=sinx的定义域为R
1.定义域
2.值域
从正弦函数的图像可以看出,正弦曲线夹在两条平行线y=1和y=-1之间,所以值域为[-1,1]
当x∈A时,函数取得最大值1,反之,若函数取得最大值1时,x∈A.
当x∈B时,函数取得最小值-1,反之,若函数取得最小值-1时,x∈B.
二、新授内容
由正弦函数图像可以看出,当自变量x的值增加2π的整数倍时,函数值重复出现,即正弦函数是周期函数,它的最小正周期是2π.
3 周期性
由于正弦函数具有周期性,为了研究问题方便,我们可以选取任意一个x值,讨论区间[x,x+ 2π]上的函数的性质,然后延拓到整个定义域上.
x
1
-1
O
二、新授内容
思考:观察正弦函数y=sinx(x∈R)的图像,能找出正弦函数的单调区间吗?
4 单调性与最值
选取区间 ,可知
在区间
在每一个区间__________________ 上是增加的;
在每一个区间__________________ 上是减少的.
二、新授内容
考点一:正弦函数的单调性及应用
探究问题:正弦函数的单调性是怎样的?
二、新授内容
考点一:正弦函数的单调性及应用
二、新授内容
考点一:正弦函数的单调性及应用
二、新授内容
考点一:正弦函数的单调性及应用
利用正弦函数单调性比较大小的步骤
(1)一定:利用诱导公式把角化到同一单调区间上.
(2)二比较:利用函数的单调性比较大小.
二、新授内容
考点一:正弦函数的单调性及应用
二、新授内容
x
y
1
-1
O
5 奇偶性
图像关于原点对称,奇函数关于原点对称.
根据诱导公式sin(-x)=sin x,可知正弦函数是奇函数
观察正弦函数的图像,可以看到
二、新授内容
6 对称性
二、新授内容
例2.画出函数y=sinx-1的图象,并讨论它的性质.
解:
函数 y=sinx-1 定义域 R 值域 [-2,0] 奇偶性 既不是奇函数,也不是偶函数 周期性 周期函数,周期是2π 单调性 在每一个闭区间 在每一个闭区间 都单调递增;
都单调递减
最大值与最小值 当 时,最大值为0; 当 时,最小值为-2 二、新授内容
考点二:正弦函数的奇偶性与周期性
二、新授内容
考点三:正弦函数的定义域与值域的应用
1:提炼知识点:
正弦函数的最值与值域
2:结合试题情境解题:
问题1:复合函数的值域怎么求?
问题2:函数y=sinx的值域是多少?
问题3:函数y何时取得最小值,何时取得最大值?
二、新授内容
【思路点拨】
考点三:图像的应用
三、反思归纳
(1)正弦函数的图像是怎样的?
(2)根据图像可以判断出正弦函数的定义域、值域、单调性、奇偶性、周期性以及对称性吗?
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
