2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 449.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 11:50:14 | ||
图片预览


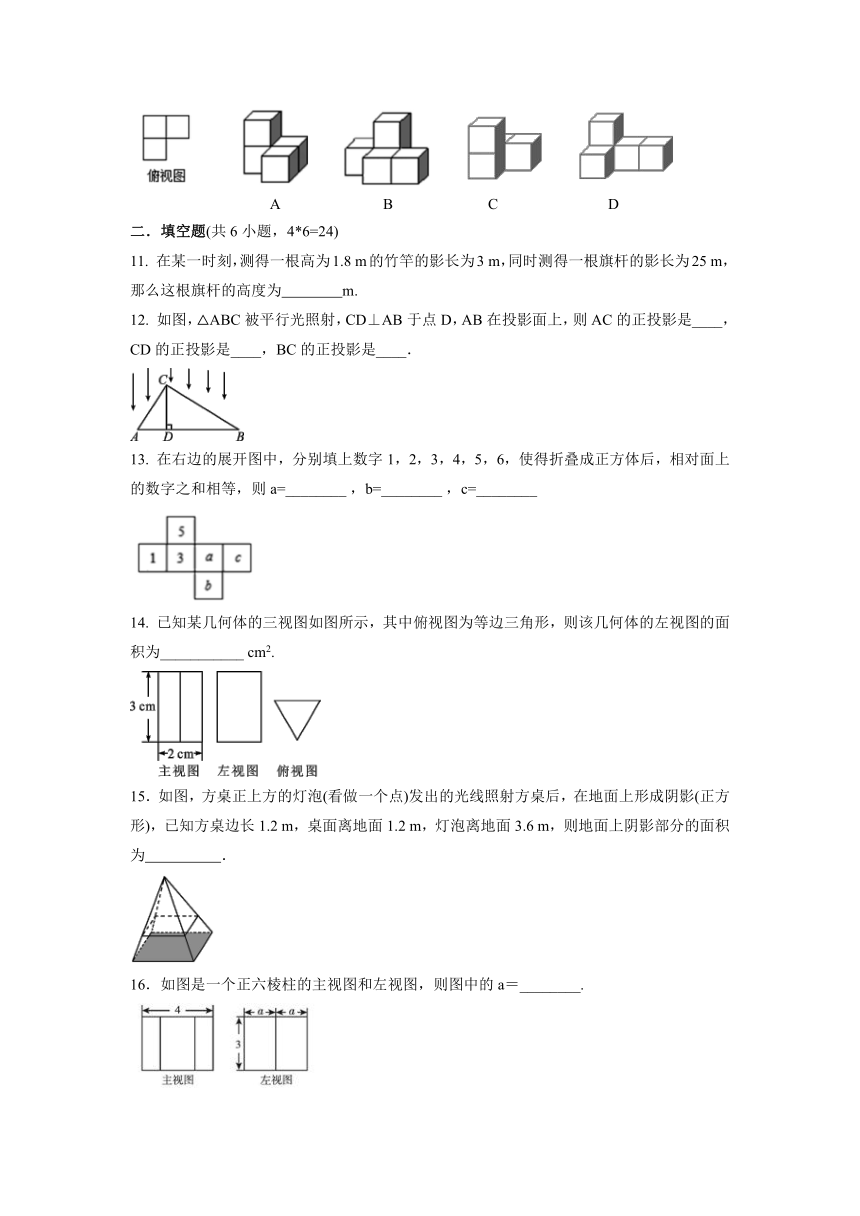
文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 如图,图中的几何体是将圆柱沿竖直方向切掉一半后,再在中心挖去一个圆柱得到的,则该几何体的左视图是( )
A B C. D
2. 在同一时刻,两根长度不等的竹竿置于阳光之下,但它们的影长相等,那么这两根竹竿的相对位置是( )
A.都垂直于地面 B.平行斜插在地上
C.不平行 D.一根倒在地上
3. 如图是某物体的三视图,则这个物体的形状是( )
A.四面体 B.直三棱柱
C.直四棱柱 D.直五棱柱
4. 下列几何体中,其主视图、左视图和俯视图完全相同的是( )
5. 如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )
A.左视图会发生改变 B.俯视图会发生改变
C.主视图会发生改变 D.三种视图都会发生改变
6. 如图,将小立方块①从6个大小相同的小立方块所搭的几何体中移走后,所得几何体( )
A.主视图改变,左视图改变
B.俯视图不变,左视图改变
C.俯视图改变,左视图改变
D.主视图不变,左视图不变
7. 下列说法正确的是( )
①平行四边形既是中心对称图形,又是轴对称图形;
②同一物体的三视图中,俯视图与左视图的宽相等;
③线段的正投影是一条线段;
④主视图是正三角形的圆锥的侧面展开图一定是半圆;
⑤图形平移的方向总是水平的,图形旋转后的效果总是不同的.
A.①③ B.②④ C.③⑤ D.②⑤
8. 有一个“田”字形的窗子,阳光照射后,地面上便呈现出它的影子,正确的是( )
A B C D
9.如图①是一个几何体的主视图和左视图.某班同学在探究它的俯视图时,画出了如图②的几个图形,其中,可能是该几何体俯视图的共有( )
A.3个 B.4个 C.5个 D.6个
10. 由几个大小相同的小正方体组成的立体图形的俯视图如左图所示,则这个立体图形应是图中的( )
A B C D
二.填空题(共6小题,4*6=24)
11. 在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一根旗杆的影长为25 m,那么这根旗杆的高度为 m.
12. 如图,△ABC被平行光照射,CD⊥AB于点D,AB在投影面上,则AC的正投影是____,CD的正投影是____,BC的正投影是____.
13. 在右边的展开图中,分别填上数字1,2,3,4,5,6,使得折叠成正方体后,相对面上的数字之和相等,则a=________ ,b=________ ,c=________
14. 已知某几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的左视图的面积为___________ cm2.
15.如图,方桌正上方的灯泡(看做一个点)发出的光线照射方桌后,在地面上形成阴影(正方形),已知方桌边长1.2 m,桌面离地面1.2 m,灯泡离地面3.6 m,则地面上阴影部分的面积为 .
16.如图是一个正六棱柱的主视图和左视图,则图中的a=________.
三.解答题(共5小题, 56分)
17.(6分) 如图,将第一行的四个物体与第二行其相应的俯视图连接起来.
18.(8分) 有两根木棒AB,CD在同一平面上直立着,其中木棒AB在太阳光下的影子
是BE,如图所示,请你在图中画出这时木棒CD的影子.
19.(8分) 某校墙边有甲、乙两根木杆,已知乙木杆的高度为1.5m.
(1)某一时刻甲木杆在阳光下的影子如图所示,画出此时乙木杆的影子DF.
(2)△ABC∽△DEF,如果测得甲、乙木杆的影子长分别为1.6m和1m,那么甲木杆的高度是多少?
20.(10分) 如图是某种几何体的三视图,
(1)这个几何体是什么;
(2)若从正面看时,长方形的宽为10m,高为20m,试求此几何体的表面积是多少m2?(结果用π表示).
21.(12分) 如图,是一个由若干同样大小的正方体搭成的几何体俯视图,小正方形中的数字表示在该位置的立方体的个数.
(1)请你画出它的从正面看和从左面看的形状图.
(2)如果每个立方体的棱长为2cm,则该几何体的表面积是多少?
22.(12分) 如图是一个几何体的三视图(单位:厘米).
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
参考答案
1-5ACBDC 6-10CBDDC
11.15
12.AD,点D,BD
13. 6,2,4
14.3
15. 3.24m2
16.
17. 解:①-c,②-a,③-b,④-d
18. 如图,连接AE,过点C作AE的平行线,过点D作BE的平行线,相交于点F,则DF即为这时木棒CD的影子.
19. (1)解:如图所示,DF是乙木杆的影子
(2)解:∵△ABC∽△DEF,∴ ,即 ,解得AB=2.4m.答:甲木杆的高度是2.4m
20. 解:(1)根据图形得到这个几何体为:圆柱,故答案为:圆柱;
(2)表面积为:2(25π)+10π×20=250π(m2)
21. 解:(1)如图所示:
(2)(2×2)×(6×2+6×2+5×2+4)=4×38=152(平方厘米).故该几何体的表面积是152平方厘米.
22. 解:(1)圆锥.
(2)设圆锥母线长为l,底面半径为r,则S表面积=S侧+S底=πrl+πr2=12π+4π=16π(平方厘米).
(3)如图,将圆锥侧面展开,线段BD为所求的最短路程,由πrl=,即12π=,解得n=120,即∠BAB′=120°,∵C为弧BB′的中点,∴∠BAD=60°,AD⊥BB′,∴BD=AB·sin 60°=6×=3(厘米).
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 如图,图中的几何体是将圆柱沿竖直方向切掉一半后,再在中心挖去一个圆柱得到的,则该几何体的左视图是( )
A B C. D
2. 在同一时刻,两根长度不等的竹竿置于阳光之下,但它们的影长相等,那么这两根竹竿的相对位置是( )
A.都垂直于地面 B.平行斜插在地上
C.不平行 D.一根倒在地上
3. 如图是某物体的三视图,则这个物体的形状是( )
A.四面体 B.直三棱柱
C.直四棱柱 D.直五棱柱
4. 下列几何体中,其主视图、左视图和俯视图完全相同的是( )
5. 如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )
A.左视图会发生改变 B.俯视图会发生改变
C.主视图会发生改变 D.三种视图都会发生改变
6. 如图,将小立方块①从6个大小相同的小立方块所搭的几何体中移走后,所得几何体( )
A.主视图改变,左视图改变
B.俯视图不变,左视图改变
C.俯视图改变,左视图改变
D.主视图不变,左视图不变
7. 下列说法正确的是( )
①平行四边形既是中心对称图形,又是轴对称图形;
②同一物体的三视图中,俯视图与左视图的宽相等;
③线段的正投影是一条线段;
④主视图是正三角形的圆锥的侧面展开图一定是半圆;
⑤图形平移的方向总是水平的,图形旋转后的效果总是不同的.
A.①③ B.②④ C.③⑤ D.②⑤
8. 有一个“田”字形的窗子,阳光照射后,地面上便呈现出它的影子,正确的是( )
A B C D
9.如图①是一个几何体的主视图和左视图.某班同学在探究它的俯视图时,画出了如图②的几个图形,其中,可能是该几何体俯视图的共有( )
A.3个 B.4个 C.5个 D.6个
10. 由几个大小相同的小正方体组成的立体图形的俯视图如左图所示,则这个立体图形应是图中的( )
A B C D
二.填空题(共6小题,4*6=24)
11. 在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一根旗杆的影长为25 m,那么这根旗杆的高度为 m.
12. 如图,△ABC被平行光照射,CD⊥AB于点D,AB在投影面上,则AC的正投影是____,CD的正投影是____,BC的正投影是____.
13. 在右边的展开图中,分别填上数字1,2,3,4,5,6,使得折叠成正方体后,相对面上的数字之和相等,则a=________ ,b=________ ,c=________
14. 已知某几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的左视图的面积为___________ cm2.
15.如图,方桌正上方的灯泡(看做一个点)发出的光线照射方桌后,在地面上形成阴影(正方形),已知方桌边长1.2 m,桌面离地面1.2 m,灯泡离地面3.6 m,则地面上阴影部分的面积为 .
16.如图是一个正六棱柱的主视图和左视图,则图中的a=________.
三.解答题(共5小题, 56分)
17.(6分) 如图,将第一行的四个物体与第二行其相应的俯视图连接起来.
18.(8分) 有两根木棒AB,CD在同一平面上直立着,其中木棒AB在太阳光下的影子
是BE,如图所示,请你在图中画出这时木棒CD的影子.
19.(8分) 某校墙边有甲、乙两根木杆,已知乙木杆的高度为1.5m.
(1)某一时刻甲木杆在阳光下的影子如图所示,画出此时乙木杆的影子DF.
(2)△ABC∽△DEF,如果测得甲、乙木杆的影子长分别为1.6m和1m,那么甲木杆的高度是多少?
20.(10分) 如图是某种几何体的三视图,
(1)这个几何体是什么;
(2)若从正面看时,长方形的宽为10m,高为20m,试求此几何体的表面积是多少m2?(结果用π表示).
21.(12分) 如图,是一个由若干同样大小的正方体搭成的几何体俯视图,小正方形中的数字表示在该位置的立方体的个数.
(1)请你画出它的从正面看和从左面看的形状图.
(2)如果每个立方体的棱长为2cm,则该几何体的表面积是多少?
22.(12分) 如图是一个几何体的三视图(单位:厘米).
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
参考答案
1-5ACBDC 6-10CBDDC
11.15
12.AD,点D,BD
13. 6,2,4
14.3
15. 3.24m2
16.
17. 解:①-c,②-a,③-b,④-d
18. 如图,连接AE,过点C作AE的平行线,过点D作BE的平行线,相交于点F,则DF即为这时木棒CD的影子.
19. (1)解:如图所示,DF是乙木杆的影子
(2)解:∵△ABC∽△DEF,∴ ,即 ,解得AB=2.4m.答:甲木杆的高度是2.4m
20. 解:(1)根据图形得到这个几何体为:圆柱,故答案为:圆柱;
(2)表面积为:2(25π)+10π×20=250π(m2)
21. 解:(1)如图所示:
(2)(2×2)×(6×2+6×2+5×2+4)=4×38=152(平方厘米).故该几何体的表面积是152平方厘米.
22. 解:(1)圆锥.
(2)设圆锥母线长为l,底面半径为r,则S表面积=S侧+S底=πrl+πr2=12π+4π=16π(平方厘米).
(3)如图,将圆锥侧面展开,线段BD为所求的最短路程,由πrl=,即12π=,解得n=120,即∠BAB′=120°,∵C为弧BB′的中点,∴∠BAD=60°,AD⊥BB′,∴BD=AB·sin 60°=6×=3(厘米).
