高中数学必修第二册人教A版-第九章 -9.2.1总体取值规律的估计课件(共39张PPT)
文档属性
| 名称 | 高中数学必修第二册人教A版-第九章 -9.2.1总体取值规律的估计课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 12:41:12 | ||
图片预览










文档简介
(共39张PPT)
9.2
9.2.1 总体取值规律的估计
用样本估计总体
第九章
学习目标
1.了解分布的意义和作用.
2.会列频率分布表,会画频率分布直方图,理解它们的特点.
3.会画条形图、扇形图、折线图等统计图,理解它们的特点.
4.会用样本的频率分布估计总体分布.
5.会用随机抽样的基本方法和用样本估计总体的思想解决一些简单的实际问题.
核心素养:数据分析、直观想象、数学运算
新知学习
知识点一 频率分布直方图
作频率分布直方图的步骤
(1)求极差:极差为一组数据中最大值与最小值的 .
(2)决定组距与组数
将数据分组时,一般取 组距,并且组距应力求“取整”,组数应力求合适,以使数据的
分布规律能较清楚地呈现出来.
(3)将数据分组
差
等长
高度
思考 要做频率分布表,需要对原始数据做哪些工作?
答案 分组,频数累计,计算频数和频率.
知识点二 其它统计图表
统计图表 主要应用
扇形图 直观描述各类数据占 的比例
条形图和直方图 直观描述不同类别或分组数据的___________
折线图 描述 随时间的变化趋势
总数
频数和频率
数据
易错辨析
1.频率分布直方图中小长方形的高表示该组上的个体在样本中出现的频率与组距的比值.( )
2.频率分布直方图中小长方形的面积表示该组的个体数.( )
3.频率分布直方图中所有小长方形面积之和为1.( )
4.样本容量越大,用样本的频率分布去估计总体的频率分布就越准确.( )
√
×
√
√
典例剖析
一、画频率分布直方图
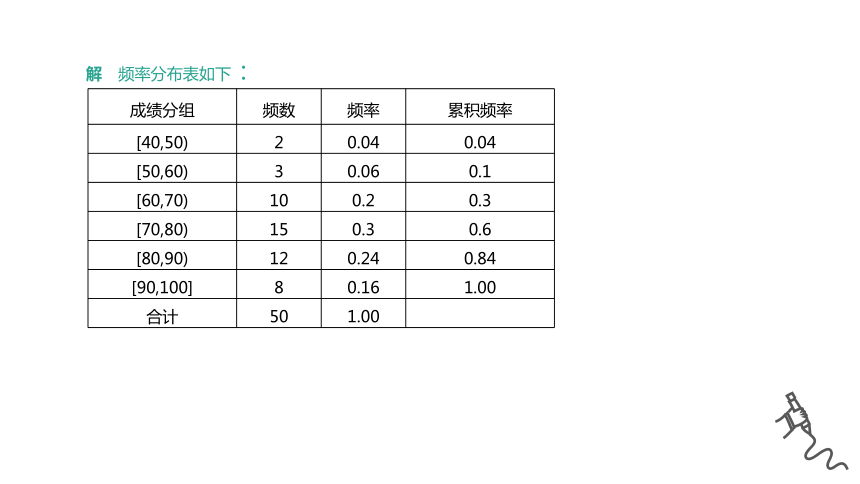
例1 从某校高三学生中抽取50名参加数学竞赛,成绩分组(单位:分)及各组的频数如下:
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表(含累积频率);
解 频率分布表如下:
成绩分组 频数 频率 累积频率
[40,50) 2 0.04 0.04
[50,60) 3 0.06 0.1
[60,70) 10 0.2 0.3
[70,80) 15 0.3 0.6
[80,90) 12 0.24 0.84
[90,100] 8 0.16 1.00
合计 50 1.00
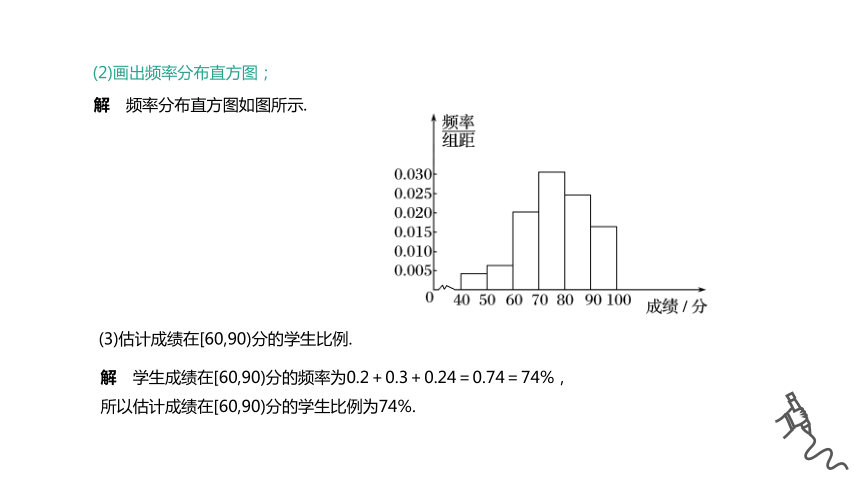
(2)画出频率分布直方图;
解 频率分布直方图如图所示.
(3)估计成绩在[60,90)分的学生比例.
解 学生成绩在[60,90)分的频率为0.2+0.3+0.24=0.74=74%,
所以估计成绩在[60,90)分的学生比例为74%.
绘制频率分布直方图的注意点
(1)各组频率的和等于1,因此,各小矩形的面积之和也等于1.
(2)同样一组数据,如果组距不同,横轴、纵轴单位不同,得到的频率分布直方图的
形状也会不同.
反思感悟
跟踪训练
为了了解九年级学生中女生的身高(单位:cm)情况,某中学对九年级部分女生身高进行了一次测量,所得数据整理后列出的频率分布表如右:
(1)求出表中m,n,M,N所表示的数分别是多少;
分组 频数 频率
[145.5,149.5) 1 0.02
[149.5,153.5) 4 0.08
[153.5,157.5) 20 0.40
[157.5,161.5) 15 0.30
[161.5,165.5) 8 0.16
[165.5,169.5] m n
合计 M N
∴m=2,M=1+4+20+15+8+2=50.
(2)画出频率分布直方图;
解 作出直角坐标系,组距为4,纵轴表示 ,横轴表示身高,画出频率分布
直方图如图所示.
(3)全体女生中身高在哪组范围内的人数最多?估计九年级学生中女
生的身高在161.5 cm以上的频率.
解 由频率分布直方图可知,样本中身高在[153.5,157.5)范围内的人数最多,且身高在161.5 cm以上的频率为0.16+0.04=0.20,由此可估计全体女生中身高在[153.5,157.5)范围内的人数最多,九年级学生中女生的身高在161.5 cm以上的频率为0.20.
二 频率分布直方图的应用
例2 为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,
将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小
矩形的面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?
样本容量是多少?
解 频率分布直方图是以面积的形式来反映数据落在各小组内的频率大小的,
(2)若次数在110以上(含110次)为达标,则该校高一年级全体学生的达标率约是多少?
反思感悟
(1)频率分布直方图的性质
①因为小矩形的面积=组距× =频率,所以各小矩形的
面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小
组内的频率大小.
②在频率分布直方图中,各小矩形的面积之和等于1.
③ =样本容量.
(2)频率分布直方图反映了样本在各个范围内取值的可能性,由抽样的代表性利用样本
在某一范围内的频率,可近似地估计总体在这一范围内的可能性.
跟踪训练
从某校随机抽取100名学生,获得了他们一周课外阅读
时间(单位:小时)的数据,整理得到数据分组及频数分
布表和频率分布直方图:
组号 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18] 2
合计 100
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的比例;
解 根据频数分布表知,100名学生中一周课外阅读时间不少于12小时的学生共有6+2+2=10(名),所以样本中的学生一周课外阅读时间少于12小时的频率是1- =0.9.
故从该校随机选取一名学生,估计其该周课外阅读时间少于12小时的比例为0.9.
组号 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18] 2
合计 100
(2)求频率分布直方图中a,b的值;
课外阅读时间落在[8,10)组内的有25人,频率为0.25,
(3)假设同一组中的每个数据可用该组区间的中点值代替,
试估计样本中的100名学生该周课外阅读时间的平均数在
第几组(只需写出结论).
解 样本中的100名学生该周课外阅读时间的平均数在
第4组.
组号 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18] 2
合计 100
三、折线图、条形图、扇形图及应用
例3 如图是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,
试根据折线统计图反映的信息,绘制该市3月1日到10日最低气温(单位:℃)的扇形统计
图和条形统计图.
解 该城市3月1日至10日的最低气温(单位:℃)情况如下表:
日期 1 2 3 4 5 6 7 8 9 10
最低气温(℃) -3 -2 0 -1 1 2 0 -1 2 2
其中最低气温为-3 ℃的有1天,占10%,最低气温为-2 ℃
的有1天,占10%,最低气温为-1 ℃的有2天,占20%,最
低气温为0 ℃的有2天,占20%,最低气温为1 ℃的有1天,
占10%,最低气温为2 ℃的有3天,占30%,扇形统计图如
图所示.
条形统计图如图所示:
(1)条形图是用一个单位长度表示一定的数量或频率,根据数量的多少或频率的大小
画成长短不同的矩形条,条形图能清楚地表示出每个项目的具体数目或频率.
(2)扇形图是用整个圆面积表示总数(100%),用圆内的扇形面积表示各个部分所占总
数的百分数.
(3)在画折线图时,要注意明确横轴、纵轴的实际含义.
反思感悟
跟踪训练
华为、抖音海外版事件暴露了我国计算机行业中芯片、软件两大短板,为防止“卡脖子”
事件的再次发生,科技专业人才就成了决胜的关键.为了解我国在芯片、软件方面的潜力,
某调查机构对我国若干大型科技公司进行调查统计,得到了这两个行业从业者的年龄分
布的饼形图和“90后”从事这两个行业的岗位分布雷达图,
则下列说法中不一定正确的是
A.芯片、软件行业从业者中,“90后”占总人数的比例超过50%
B.芯片、软件行业中从事技术、设计岗位的“90后”人数超过总人数的25%
C.芯片、软件行业从事技术岗位的人中,“90后”比“80后”多
D.芯片、软件行业中,“90后”从事市场岗位的人数比“80前”的总人数多
C解析 对于选项A,芯片、软件行业从业者中“90后”占总人数的55%,故选项A正确;
对于选项B,芯片、软件行业中从事技术、设计岗位的“90后”占总人数的(37%+13%)
×55%=27.5%,故选项B正确;对于选项C,芯片、软件行业中从事技术岗位的“90后”
占总人数的37%×55%=20.35%,“80后”占总人数的40%,但从事技术的“80后”占总
人数的百分比不知道,无法确定二者人数多少,故选项C错误;对于选项D,芯片、
软件行业中从事市场岗位的“90后”占总人数的14%×55%=7.7%,“80前”占总人数的5%,
故选项D正确.
随堂小测
1.用样本频率分布估计总体频率分布的过程中,下列说法正确的是
A.总体容量越大,估计越精确
B.总体容量越小,估计越精确
C.样本容量越大,估计越精确
D.样本容量越小,估计越精确
C解析 用样本的频率分布估计总体的频率分布时,在总体一定时,样本的容量越
大,估计就越精确.
2.一个容量为20的样本数据,分组与频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则样本在[10,50)内的频率为
A.0.5 B.0.24 C.0.6 D.0.7
D解析 因为样本在[10,50)内的频数为2+3+4+5=14,样本容量为20,
3.(多选)容量为100的样本,其数据分布在[2,18]内,将样本数据分为4组:[2,6),
[6,10),[10,14),[14,18],得到频率分布直方图如图所示,则下列说法中
正确的是
A.样本数据分布在[6,10)内的频率为0.32
B.样本数据分布在[10,14)内的频数为40
C.样本数据分布在[2,10)内的频数为40
D.估计总体数据大约有10%分布在[10,14)内
对于C,由题图可得,样本数据分布在[2,10)内的频数为
100×(0.02+0.08)×4=40,所以C正确.
对于D,由题图可估计,总体数据分布在[10,14)内的比例为0.1×4=0.4=40%,所以
D错误,故选ABC.
ABC解析 对于A,由题图可得,样本数据分布在[6,10)
内的频率为0.08×4=0.32,所以A正确.
对于B,由题图可得,样本数据分布在[10,14)内的频数
为100×(0.1×4)=40,所以B正确.
4.某地政府调查了工薪阶层1 000人的月工资,并根据调查结
果画出如图所示的频率分布直方图,为了了解工薪阶层对月工
资的满意程度,要用分层随机抽样的方法从调查的1 000人中
抽出100人做电话询访,则月工资在区间[30,35)内的工薪阶
层应抽出_____人.
15
解析 月工资落在区间[30,35)内的频率为
1-(0.02+0.04+0.05+0.05+0.01)×5=0.15,
所以月工资在区间[30,35)内的工薪阶层应抽出100×0.15=15(人).
5.为了解今年某校高三毕业班准备报考飞行员学生的体重(单位:千克)情况,将所得的
数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前三个小组的
频率之比为1∶2∶3,其中第2小组的频数为12.则该校报考飞行员的总人数为_____.
48
解析 设报考飞行员的总人数为n,
设第1小组的频率为a,
则有a+2a+3a+(0.013+0.037)×5=1,
解得a=0.125,
所以第2小组的频率为0.25.
又第2小组的频数为12,
课堂小结
1.知识清单:
(1)频数与频率.
(2)频率分布表.
(3)频率分布直方图.
(4)扇形图、条形图和折线图.
2.方法归纳:图表识别、数据分析.
3.常见误区:频率分布直方图中小矩形的高以及小矩形的面积代表的意义理解不清.
Thank you for watching !
9.2
9.2.1 总体取值规律的估计
用样本估计总体
第九章
学习目标
1.了解分布的意义和作用.
2.会列频率分布表,会画频率分布直方图,理解它们的特点.
3.会画条形图、扇形图、折线图等统计图,理解它们的特点.
4.会用样本的频率分布估计总体分布.
5.会用随机抽样的基本方法和用样本估计总体的思想解决一些简单的实际问题.
核心素养:数据分析、直观想象、数学运算
新知学习
知识点一 频率分布直方图
作频率分布直方图的步骤
(1)求极差:极差为一组数据中最大值与最小值的 .
(2)决定组距与组数
将数据分组时,一般取 组距,并且组距应力求“取整”,组数应力求合适,以使数据的
分布规律能较清楚地呈现出来.
(3)将数据分组
差
等长
高度
思考 要做频率分布表,需要对原始数据做哪些工作?
答案 分组,频数累计,计算频数和频率.
知识点二 其它统计图表
统计图表 主要应用
扇形图 直观描述各类数据占 的比例
条形图和直方图 直观描述不同类别或分组数据的___________
折线图 描述 随时间的变化趋势
总数
频数和频率
数据
易错辨析
1.频率分布直方图中小长方形的高表示该组上的个体在样本中出现的频率与组距的比值.( )
2.频率分布直方图中小长方形的面积表示该组的个体数.( )
3.频率分布直方图中所有小长方形面积之和为1.( )
4.样本容量越大,用样本的频率分布去估计总体的频率分布就越准确.( )
√
×
√
√
典例剖析
一、画频率分布直方图
例1 从某校高三学生中抽取50名参加数学竞赛,成绩分组(单位:分)及各组的频数如下:
[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表(含累积频率);
解 频率分布表如下:
成绩分组 频数 频率 累积频率
[40,50) 2 0.04 0.04
[50,60) 3 0.06 0.1
[60,70) 10 0.2 0.3
[70,80) 15 0.3 0.6
[80,90) 12 0.24 0.84
[90,100] 8 0.16 1.00
合计 50 1.00
(2)画出频率分布直方图;
解 频率分布直方图如图所示.
(3)估计成绩在[60,90)分的学生比例.
解 学生成绩在[60,90)分的频率为0.2+0.3+0.24=0.74=74%,
所以估计成绩在[60,90)分的学生比例为74%.
绘制频率分布直方图的注意点
(1)各组频率的和等于1,因此,各小矩形的面积之和也等于1.
(2)同样一组数据,如果组距不同,横轴、纵轴单位不同,得到的频率分布直方图的
形状也会不同.
反思感悟
跟踪训练
为了了解九年级学生中女生的身高(单位:cm)情况,某中学对九年级部分女生身高进行了一次测量,所得数据整理后列出的频率分布表如右:
(1)求出表中m,n,M,N所表示的数分别是多少;
分组 频数 频率
[145.5,149.5) 1 0.02
[149.5,153.5) 4 0.08
[153.5,157.5) 20 0.40
[157.5,161.5) 15 0.30
[161.5,165.5) 8 0.16
[165.5,169.5] m n
合计 M N
∴m=2,M=1+4+20+15+8+2=50.
(2)画出频率分布直方图;
解 作出直角坐标系,组距为4,纵轴表示 ,横轴表示身高,画出频率分布
直方图如图所示.
(3)全体女生中身高在哪组范围内的人数最多?估计九年级学生中女
生的身高在161.5 cm以上的频率.
解 由频率分布直方图可知,样本中身高在[153.5,157.5)范围内的人数最多,且身高在161.5 cm以上的频率为0.16+0.04=0.20,由此可估计全体女生中身高在[153.5,157.5)范围内的人数最多,九年级学生中女生的身高在161.5 cm以上的频率为0.20.
二 频率分布直方图的应用
例2 为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,
将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小
矩形的面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?
样本容量是多少?
解 频率分布直方图是以面积的形式来反映数据落在各小组内的频率大小的,
(2)若次数在110以上(含110次)为达标,则该校高一年级全体学生的达标率约是多少?
反思感悟
(1)频率分布直方图的性质
①因为小矩形的面积=组距× =频率,所以各小矩形的
面积表示相应各组的频率.这样,频率分布直方图就以面积的形式反映了数据落在各个小
组内的频率大小.
②在频率分布直方图中,各小矩形的面积之和等于1.
③ =样本容量.
(2)频率分布直方图反映了样本在各个范围内取值的可能性,由抽样的代表性利用样本
在某一范围内的频率,可近似地估计总体在这一范围内的可能性.
跟踪训练
从某校随机抽取100名学生,获得了他们一周课外阅读
时间(单位:小时)的数据,整理得到数据分组及频数分
布表和频率分布直方图:
组号 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18] 2
合计 100
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的比例;
解 根据频数分布表知,100名学生中一周课外阅读时间不少于12小时的学生共有6+2+2=10(名),所以样本中的学生一周课外阅读时间少于12小时的频率是1- =0.9.
故从该校随机选取一名学生,估计其该周课外阅读时间少于12小时的比例为0.9.
组号 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18] 2
合计 100
(2)求频率分布直方图中a,b的值;
课外阅读时间落在[8,10)组内的有25人,频率为0.25,
(3)假设同一组中的每个数据可用该组区间的中点值代替,
试估计样本中的100名学生该周课外阅读时间的平均数在
第几组(只需写出结论).
解 样本中的100名学生该周课外阅读时间的平均数在
第4组.
组号 分组 频数
1 [0,2) 6
2 [2,4) 8
3 [4,6) 17
4 [6,8) 22
5 [8,10) 25
6 [10,12) 12
7 [12,14) 6
8 [14,16) 2
9 [16,18] 2
合计 100
三、折线图、条形图、扇形图及应用
例3 如图是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,
试根据折线统计图反映的信息,绘制该市3月1日到10日最低气温(单位:℃)的扇形统计
图和条形统计图.
解 该城市3月1日至10日的最低气温(单位:℃)情况如下表:
日期 1 2 3 4 5 6 7 8 9 10
最低气温(℃) -3 -2 0 -1 1 2 0 -1 2 2
其中最低气温为-3 ℃的有1天,占10%,最低气温为-2 ℃
的有1天,占10%,最低气温为-1 ℃的有2天,占20%,最
低气温为0 ℃的有2天,占20%,最低气温为1 ℃的有1天,
占10%,最低气温为2 ℃的有3天,占30%,扇形统计图如
图所示.
条形统计图如图所示:
(1)条形图是用一个单位长度表示一定的数量或频率,根据数量的多少或频率的大小
画成长短不同的矩形条,条形图能清楚地表示出每个项目的具体数目或频率.
(2)扇形图是用整个圆面积表示总数(100%),用圆内的扇形面积表示各个部分所占总
数的百分数.
(3)在画折线图时,要注意明确横轴、纵轴的实际含义.
反思感悟
跟踪训练
华为、抖音海外版事件暴露了我国计算机行业中芯片、软件两大短板,为防止“卡脖子”
事件的再次发生,科技专业人才就成了决胜的关键.为了解我国在芯片、软件方面的潜力,
某调查机构对我国若干大型科技公司进行调查统计,得到了这两个行业从业者的年龄分
布的饼形图和“90后”从事这两个行业的岗位分布雷达图,
则下列说法中不一定正确的是
A.芯片、软件行业从业者中,“90后”占总人数的比例超过50%
B.芯片、软件行业中从事技术、设计岗位的“90后”人数超过总人数的25%
C.芯片、软件行业从事技术岗位的人中,“90后”比“80后”多
D.芯片、软件行业中,“90后”从事市场岗位的人数比“80前”的总人数多
C解析 对于选项A,芯片、软件行业从业者中“90后”占总人数的55%,故选项A正确;
对于选项B,芯片、软件行业中从事技术、设计岗位的“90后”占总人数的(37%+13%)
×55%=27.5%,故选项B正确;对于选项C,芯片、软件行业中从事技术岗位的“90后”
占总人数的37%×55%=20.35%,“80后”占总人数的40%,但从事技术的“80后”占总
人数的百分比不知道,无法确定二者人数多少,故选项C错误;对于选项D,芯片、
软件行业中从事市场岗位的“90后”占总人数的14%×55%=7.7%,“80前”占总人数的5%,
故选项D正确.
随堂小测
1.用样本频率分布估计总体频率分布的过程中,下列说法正确的是
A.总体容量越大,估计越精确
B.总体容量越小,估计越精确
C.样本容量越大,估计越精确
D.样本容量越小,估计越精确
C解析 用样本的频率分布估计总体的频率分布时,在总体一定时,样本的容量越
大,估计就越精确.
2.一个容量为20的样本数据,分组与频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则样本在[10,50)内的频率为
A.0.5 B.0.24 C.0.6 D.0.7
D解析 因为样本在[10,50)内的频数为2+3+4+5=14,样本容量为20,
3.(多选)容量为100的样本,其数据分布在[2,18]内,将样本数据分为4组:[2,6),
[6,10),[10,14),[14,18],得到频率分布直方图如图所示,则下列说法中
正确的是
A.样本数据分布在[6,10)内的频率为0.32
B.样本数据分布在[10,14)内的频数为40
C.样本数据分布在[2,10)内的频数为40
D.估计总体数据大约有10%分布在[10,14)内
对于C,由题图可得,样本数据分布在[2,10)内的频数为
100×(0.02+0.08)×4=40,所以C正确.
对于D,由题图可估计,总体数据分布在[10,14)内的比例为0.1×4=0.4=40%,所以
D错误,故选ABC.
ABC解析 对于A,由题图可得,样本数据分布在[6,10)
内的频率为0.08×4=0.32,所以A正确.
对于B,由题图可得,样本数据分布在[10,14)内的频数
为100×(0.1×4)=40,所以B正确.
4.某地政府调查了工薪阶层1 000人的月工资,并根据调查结
果画出如图所示的频率分布直方图,为了了解工薪阶层对月工
资的满意程度,要用分层随机抽样的方法从调查的1 000人中
抽出100人做电话询访,则月工资在区间[30,35)内的工薪阶
层应抽出_____人.
15
解析 月工资落在区间[30,35)内的频率为
1-(0.02+0.04+0.05+0.05+0.01)×5=0.15,
所以月工资在区间[30,35)内的工薪阶层应抽出100×0.15=15(人).
5.为了解今年某校高三毕业班准备报考飞行员学生的体重(单位:千克)情况,将所得的
数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前三个小组的
频率之比为1∶2∶3,其中第2小组的频数为12.则该校报考飞行员的总人数为_____.
48
解析 设报考飞行员的总人数为n,
设第1小组的频率为a,
则有a+2a+3a+(0.013+0.037)×5=1,
解得a=0.125,
所以第2小组的频率为0.25.
又第2小组的频数为12,
课堂小结
1.知识清单:
(1)频数与频率.
(2)频率分布表.
(3)频率分布直方图.
(4)扇形图、条形图和折线图.
2.方法归纳:图表识别、数据分析.
3.常见误区:频率分布直方图中小矩形的高以及小矩形的面积代表的意义理解不清.
Thank you for watching !
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
