人教版六年级下册3.1圆柱同步练习(含答案)
文档属性
| 名称 | 人教版六年级下册3.1圆柱同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 69.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 06:56:44 | ||
图片预览




文档简介
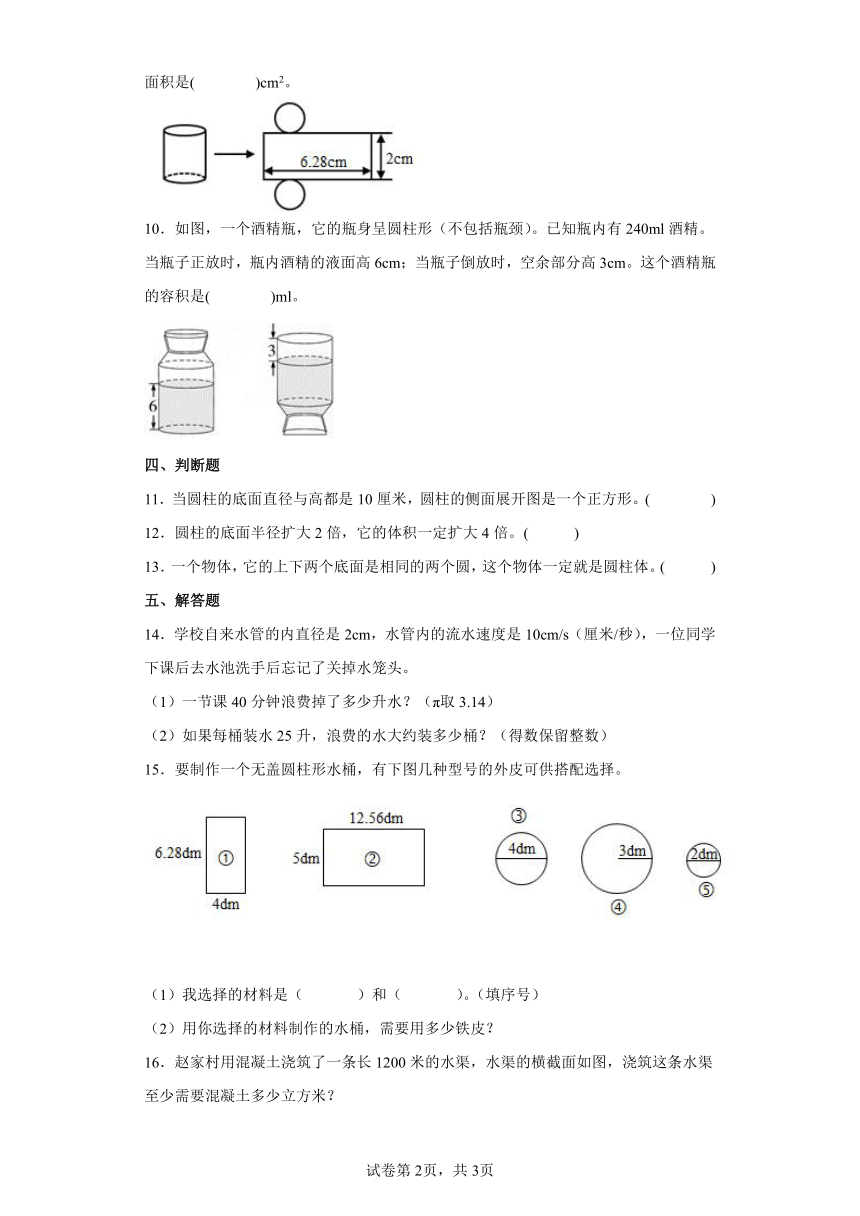
人教版六年级下册 3.1 圆柱 同步练习
一、选择题
1.压路机滚筒滚动一周能压多少路面是求滚筒的( )。
A.表面积 B.侧面积 C.体积
2.一根圆木锯成2段,一共增加( )个圆面。
A.2 B.4 C.6
3.圆柱的高不变,底面半径缩小为原来的,圆柱的体积( )。
A.缩小为原来的 B.缩小为原来的 C.不变
4.营养学家建议:儿童每天喝水的摄入量约为1500毫升,要达到这个要求,小明每天用底面直径8cm,高10cm的圆柱形水杯喝水,他约喝( )杯水比较好。
A.2 B.3 C.4 D.5
5.下面各图是圆柱的展开图的是( )。
A. B. C. D.
二、图形计算
6.求圆柱的表面积?
7.求圆柱的表面积和体积。(单位:cm)
三、填空题
8.一个底面积为x平方厘米、高为h厘米的圆柱切成若干个小圆柱。每切1次,表面积都增加( )平方厘米,切5次表面积增加( )平方厘米。
9.如图,要计算圆柱的表面积,就要分别求出圆柱的( )和( ),它的表面积是( )cm2。
10.如图,一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈)。已知瓶内有240ml酒精。当瓶子正放时,瓶内酒精的液面高6cm;当瓶子倒放时,空余部分高3cm。这个酒精瓶的容积是( )ml。
四、判断题
11.当圆柱的底面直径与高都是10厘米,圆柱的侧面展开图是一个正方形。( )
12.圆柱的底面半径扩大2倍,它的体积一定扩大4倍。( )
13.一个物体,它的上下两个底面是相同的两个圆,这个物体一定就是圆柱体。( )
五、解答题
14.学校自来水管的内直径是2cm,水管内的流水速度是10cm/s(厘米/秒),一位同学下课后去水池洗手后忘记了关掉水笼头。
(1)一节课40分钟浪费掉了多少升水?(π取3.14)
(2)如果每桶装水25升,浪费的水大约装多少桶?(得数保留整数)
15.要制作一个无盖圆柱形水桶,有下图几种型号的外皮可供搭配选择。
(1)我选择的材料是( )和( )。(填序号)
(2)用你选择的材料制作的水桶,需要用多少铁皮?
16.赵家村用混凝土浇筑了一条长1200米的水渠,水渠的横截面如图,浇筑这条水渠至少需要混凝土多少立方米?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
压路机滚筒在地上滚动一周所压的路面是一个长方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高,因为“圆柱的侧面积=底面周长×高”,所以在地上滚动一周所压的路面正好是压路机滚筒的侧面积;进而得出结论。
【详解】
由分析可知:
压路机滚筒滚动一周能压多少路面是求滚筒的侧面积。
故选:B
【点睛】
此题考查了圆柱的侧面展开图,应明确压路机滚筒在地上滚动一周所压的路面是一个长方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高。
2.A
【解析】
【分析】
一根圆木每锯一下就会新露出2个横截面,据此解答。
【详解】
一根圆木锯成2段,一共增加2个圆面。
故选:A。
【点睛】
新露出横截面的个数(段数-1)×2。
3.B
【解析】
【分析】
设圆柱的半径为1,高为1,由此利用圆柱的体积公式分别求出扩大前后的体积进行比较即可选择。
【详解】
设圆柱的半径为1,高为1,
则圆柱的体积为:π×12×1=π;
若半径缩小为原来的,则圆柱的体积为:;
,所以它的体积是缩小为原来的,
故答案为:B
【点睛】
此题考查了圆柱的体积公式的灵活应用,熟记公式是解题的关键。
4.B
【解析】
【分析】
根据水杯的底面直径和高计算出水杯的容积,小明喝水的杯数=1500毫升÷水杯的容积,据此解答。
【详解】
3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方厘米)
502.4立方厘米=502.4毫升
1500÷502.4≈3(杯)
故答案为:B
【点睛】
掌握圆柱的体积计算方法是解答题目的关键。
5.C
【解析】
【分析】
圆柱侧面展开图是个长方形,长方形的长=圆柱底面周长,据此分析。
【详解】
3.14×6=18.84
故答案为:C
【点睛】
关键是熟悉圆柱特征,理解侧面展开图与底面之间的关系。
6.87.92平方米
【解析】
【分析】
圆柱的侧面积=底面周长×高,圆柱的表面积=圆的侧面积+两个底面积,据此解答即可。
【详解】
侧面积:3.14×2×2×5
=12.56×5
=62.8(平方米)
表面积:62.8+3.14×22×2
=62.8+25.12
=87.92(平方米)
7.785平方厘米;1570立方厘米
【解析】
【分析】
圆柱表面积=底面积×2+侧面积,圆柱体积=底面积×高,据此列式计算。
【详解】
10÷2=5(厘米)
3.14×52×2+3.14×10×20
=157+628
=785(平方厘米)
3.14×52×20
=78.5×20
=1570(立方厘米)
8. 2x 10x
【解析】
【分析】
一个圆柱每切1次表面积就增加2个截面的面积,切5次表面积增加(2×5)个截面的面积,截面面积为x平方厘米,据此解答。
【详解】
一个底面积为x平方厘米、高为h厘米的圆柱切成若干个小圆柱。每切1次,表面积都增加( 2x )平方厘米,切5次表面积增加( 10x )平方厘米。
【点睛】
切圆柱体时,增加截面的个数是切的次数的2倍。
9. 侧面积 两个底面积和 18.84
【解析】
【分析】
圆柱表面积=侧面积+底面积×2,据此分析。
【详解】
6.28÷3.14÷2=1(厘米)
6.28×2+3.14×1 ×2
=12.56+6.28
=18.84(平方厘米)
要计算圆柱的表面积,就要分别求出圆柱的侧面积和两个底面积和,它的表面积是18.84cm2。
【点睛】
关键是掌握圆柱表面积公式,圆柱侧面积=底面周长×高。
10.360
【解析】
【分析】
空余部分容积相等,用酒精体积÷高=底面积,底面积×3厘米=空白部分容积,酒精体积+空白部分容积=酒精瓶的容积。
【详解】
240÷6=40(平方厘米)
40×3=120(立方厘米)
240+120=360(立方厘米)=360(毫升)
【点睛】
关键是掌握圆柱体积公式,圆柱体积=底面积×高。
11.×
【解析】
【分析】
根据圆的周长公式,求出圆柱的底面周长。圆柱的侧面展开图是以底面周长和高为长宽的长方形,据此判断底面周长和高是否相等,从而判断圆柱侧面展开图是否是正方形。
【详解】
底面周长:3.14×10=31.4(厘米)
由于底面周长和高不相等,所以这个圆柱的侧面展开图不是一个正方形。
所以判断错误。
【点睛】
本题考查了圆柱的侧面展开图,有一定空间思维是解题的关键。
12.×
【解析】
【分析】
圆柱的体积=底面积×高,圆柱的底面半径扩大2倍,底面积扩大4倍,如果高不变,它的体积就扩大4倍,据此判断。
【详解】
因为圆柱的体积是由底面积和高两个条件决定的,圆柱的底面半径扩大2倍,底面积扩大4倍,如果高不变,它的体积就扩大4倍。本题没有说明高不变,因此这种说法是错误的。
故答案为:×。
【点睛】
本题考查圆柱的体积,解答本题的关键是掌握圆柱的体积计算公式。
13.×
【解析】
【分析】
因为圆柱每个横截面都是相等的,而不止是上下两个面相等,且圆柱的侧面展开是一个长方形,如:生活中我们认识的腰鼓,上下两个面都是相等的圆,但它不是圆柱体,所以一个物体,它的上下两个底面是相同的两个圆,它可能不是圆柱体;据此判断。
【详解】
一个物体,它的上下两个底面是相同的两个圆,这个物体一定就是圆柱体;
此说法是错误的;
故答案为:×。
【点睛】
本题考查圆柱,解答本题的关键是掌握圆柱的特征。
14.(1)75.36升;
(2)4桶
【解析】
【分析】
(1)利用圆柱的体积计算公式求出每秒浪费水的体积,再用乘法计算出40分钟浪费水的体积,把结果转化为升;
(2)浪费水的桶数=浪费水的总升数÷每桶装水的升数,结果用进一法保留整数,据此解答。
【详解】
(1)40×60=2400(秒)
3.14×(2÷2)2×10×2400
=3.14×1×10×2400
=31.4×2400
=75360(立方厘米)
75360立方厘米=75.36升
答:一节课40分钟浪费掉了75.36升水。
(2)75.36÷25≈4(桶)
答;浪费的水大约装4桶。
【点睛】
掌握圆柱的体积计算公式是解答题目的关键。
15.(1)②和③
(2)75.36平方分米
【解析】
【分析】
根据圆柱的侧面展开图可知,圆柱的侧面展开后是一个长方形,该长方形的长等于底面周长,然后根据圆柱的表面积=底面圆的面积+侧面长方形的面积,据此解答即可。
【详解】
(1)③号圆的周长:3.14×4=12.56(dm)
②号长方形的长为12.56,刚好可以围成一个圆柱。
所以我选择的材料是( ② )和( ③ )。
(2)12.56×5+3.14×(4÷2)2
=62.8+3.14×4
=62.8+12.56
=75.36(平方分米)
答:需要用75.36平方分米的铁皮。
【点睛】
本题考查圆柱的表面积,熟记公式是解题的关键。
16.10464立方米
【解析】
【分析】
需要混凝土的体积=水渠的长度×(梯形的面积-半圆的面积),据此解答。
【详解】
[(4+6)×3÷2-×3.14×(4÷2)2]×1200
=[10×3÷2-×3.14×4]×1200
=[15-6.28]×1200
=8.72×1200
=10464(立方米)
答:浇筑这条水渠至少需要混凝土10464立方米。
【点睛】
分析图形求出横截面的面积是解答题目的关键。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.压路机滚筒滚动一周能压多少路面是求滚筒的( )。
A.表面积 B.侧面积 C.体积
2.一根圆木锯成2段,一共增加( )个圆面。
A.2 B.4 C.6
3.圆柱的高不变,底面半径缩小为原来的,圆柱的体积( )。
A.缩小为原来的 B.缩小为原来的 C.不变
4.营养学家建议:儿童每天喝水的摄入量约为1500毫升,要达到这个要求,小明每天用底面直径8cm,高10cm的圆柱形水杯喝水,他约喝( )杯水比较好。
A.2 B.3 C.4 D.5
5.下面各图是圆柱的展开图的是( )。
A. B. C. D.
二、图形计算
6.求圆柱的表面积?
7.求圆柱的表面积和体积。(单位:cm)
三、填空题
8.一个底面积为x平方厘米、高为h厘米的圆柱切成若干个小圆柱。每切1次,表面积都增加( )平方厘米,切5次表面积增加( )平方厘米。
9.如图,要计算圆柱的表面积,就要分别求出圆柱的( )和( ),它的表面积是( )cm2。
10.如图,一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈)。已知瓶内有240ml酒精。当瓶子正放时,瓶内酒精的液面高6cm;当瓶子倒放时,空余部分高3cm。这个酒精瓶的容积是( )ml。
四、判断题
11.当圆柱的底面直径与高都是10厘米,圆柱的侧面展开图是一个正方形。( )
12.圆柱的底面半径扩大2倍,它的体积一定扩大4倍。( )
13.一个物体,它的上下两个底面是相同的两个圆,这个物体一定就是圆柱体。( )
五、解答题
14.学校自来水管的内直径是2cm,水管内的流水速度是10cm/s(厘米/秒),一位同学下课后去水池洗手后忘记了关掉水笼头。
(1)一节课40分钟浪费掉了多少升水?(π取3.14)
(2)如果每桶装水25升,浪费的水大约装多少桶?(得数保留整数)
15.要制作一个无盖圆柱形水桶,有下图几种型号的外皮可供搭配选择。
(1)我选择的材料是( )和( )。(填序号)
(2)用你选择的材料制作的水桶,需要用多少铁皮?
16.赵家村用混凝土浇筑了一条长1200米的水渠,水渠的横截面如图,浇筑这条水渠至少需要混凝土多少立方米?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
压路机滚筒在地上滚动一周所压的路面是一个长方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高,因为“圆柱的侧面积=底面周长×高”,所以在地上滚动一周所压的路面正好是压路机滚筒的侧面积;进而得出结论。
【详解】
由分析可知:
压路机滚筒滚动一周能压多少路面是求滚筒的侧面积。
故选:B
【点睛】
此题考查了圆柱的侧面展开图,应明确压路机滚筒在地上滚动一周所压的路面是一个长方形,长方形的长等于圆柱的底面周长,宽等于圆柱的高。
2.A
【解析】
【分析】
一根圆木每锯一下就会新露出2个横截面,据此解答。
【详解】
一根圆木锯成2段,一共增加2个圆面。
故选:A。
【点睛】
新露出横截面的个数(段数-1)×2。
3.B
【解析】
【分析】
设圆柱的半径为1,高为1,由此利用圆柱的体积公式分别求出扩大前后的体积进行比较即可选择。
【详解】
设圆柱的半径为1,高为1,
则圆柱的体积为:π×12×1=π;
若半径缩小为原来的,则圆柱的体积为:;
,所以它的体积是缩小为原来的,
故答案为:B
【点睛】
此题考查了圆柱的体积公式的灵活应用,熟记公式是解题的关键。
4.B
【解析】
【分析】
根据水杯的底面直径和高计算出水杯的容积,小明喝水的杯数=1500毫升÷水杯的容积,据此解答。
【详解】
3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方厘米)
502.4立方厘米=502.4毫升
1500÷502.4≈3(杯)
故答案为:B
【点睛】
掌握圆柱的体积计算方法是解答题目的关键。
5.C
【解析】
【分析】
圆柱侧面展开图是个长方形,长方形的长=圆柱底面周长,据此分析。
【详解】
3.14×6=18.84
故答案为:C
【点睛】
关键是熟悉圆柱特征,理解侧面展开图与底面之间的关系。
6.87.92平方米
【解析】
【分析】
圆柱的侧面积=底面周长×高,圆柱的表面积=圆的侧面积+两个底面积,据此解答即可。
【详解】
侧面积:3.14×2×2×5
=12.56×5
=62.8(平方米)
表面积:62.8+3.14×22×2
=62.8+25.12
=87.92(平方米)
7.785平方厘米;1570立方厘米
【解析】
【分析】
圆柱表面积=底面积×2+侧面积,圆柱体积=底面积×高,据此列式计算。
【详解】
10÷2=5(厘米)
3.14×52×2+3.14×10×20
=157+628
=785(平方厘米)
3.14×52×20
=78.5×20
=1570(立方厘米)
8. 2x 10x
【解析】
【分析】
一个圆柱每切1次表面积就增加2个截面的面积,切5次表面积增加(2×5)个截面的面积,截面面积为x平方厘米,据此解答。
【详解】
一个底面积为x平方厘米、高为h厘米的圆柱切成若干个小圆柱。每切1次,表面积都增加( 2x )平方厘米,切5次表面积增加( 10x )平方厘米。
【点睛】
切圆柱体时,增加截面的个数是切的次数的2倍。
9. 侧面积 两个底面积和 18.84
【解析】
【分析】
圆柱表面积=侧面积+底面积×2,据此分析。
【详解】
6.28÷3.14÷2=1(厘米)
6.28×2+3.14×1 ×2
=12.56+6.28
=18.84(平方厘米)
要计算圆柱的表面积,就要分别求出圆柱的侧面积和两个底面积和,它的表面积是18.84cm2。
【点睛】
关键是掌握圆柱表面积公式,圆柱侧面积=底面周长×高。
10.360
【解析】
【分析】
空余部分容积相等,用酒精体积÷高=底面积,底面积×3厘米=空白部分容积,酒精体积+空白部分容积=酒精瓶的容积。
【详解】
240÷6=40(平方厘米)
40×3=120(立方厘米)
240+120=360(立方厘米)=360(毫升)
【点睛】
关键是掌握圆柱体积公式,圆柱体积=底面积×高。
11.×
【解析】
【分析】
根据圆的周长公式,求出圆柱的底面周长。圆柱的侧面展开图是以底面周长和高为长宽的长方形,据此判断底面周长和高是否相等,从而判断圆柱侧面展开图是否是正方形。
【详解】
底面周长:3.14×10=31.4(厘米)
由于底面周长和高不相等,所以这个圆柱的侧面展开图不是一个正方形。
所以判断错误。
【点睛】
本题考查了圆柱的侧面展开图,有一定空间思维是解题的关键。
12.×
【解析】
【分析】
圆柱的体积=底面积×高,圆柱的底面半径扩大2倍,底面积扩大4倍,如果高不变,它的体积就扩大4倍,据此判断。
【详解】
因为圆柱的体积是由底面积和高两个条件决定的,圆柱的底面半径扩大2倍,底面积扩大4倍,如果高不变,它的体积就扩大4倍。本题没有说明高不变,因此这种说法是错误的。
故答案为:×。
【点睛】
本题考查圆柱的体积,解答本题的关键是掌握圆柱的体积计算公式。
13.×
【解析】
【分析】
因为圆柱每个横截面都是相等的,而不止是上下两个面相等,且圆柱的侧面展开是一个长方形,如:生活中我们认识的腰鼓,上下两个面都是相等的圆,但它不是圆柱体,所以一个物体,它的上下两个底面是相同的两个圆,它可能不是圆柱体;据此判断。
【详解】
一个物体,它的上下两个底面是相同的两个圆,这个物体一定就是圆柱体;
此说法是错误的;
故答案为:×。
【点睛】
本题考查圆柱,解答本题的关键是掌握圆柱的特征。
14.(1)75.36升;
(2)4桶
【解析】
【分析】
(1)利用圆柱的体积计算公式求出每秒浪费水的体积,再用乘法计算出40分钟浪费水的体积,把结果转化为升;
(2)浪费水的桶数=浪费水的总升数÷每桶装水的升数,结果用进一法保留整数,据此解答。
【详解】
(1)40×60=2400(秒)
3.14×(2÷2)2×10×2400
=3.14×1×10×2400
=31.4×2400
=75360(立方厘米)
75360立方厘米=75.36升
答:一节课40分钟浪费掉了75.36升水。
(2)75.36÷25≈4(桶)
答;浪费的水大约装4桶。
【点睛】
掌握圆柱的体积计算公式是解答题目的关键。
15.(1)②和③
(2)75.36平方分米
【解析】
【分析】
根据圆柱的侧面展开图可知,圆柱的侧面展开后是一个长方形,该长方形的长等于底面周长,然后根据圆柱的表面积=底面圆的面积+侧面长方形的面积,据此解答即可。
【详解】
(1)③号圆的周长:3.14×4=12.56(dm)
②号长方形的长为12.56,刚好可以围成一个圆柱。
所以我选择的材料是( ② )和( ③ )。
(2)12.56×5+3.14×(4÷2)2
=62.8+3.14×4
=62.8+12.56
=75.36(平方分米)
答:需要用75.36平方分米的铁皮。
【点睛】
本题考查圆柱的表面积,熟记公式是解题的关键。
16.10464立方米
【解析】
【分析】
需要混凝土的体积=水渠的长度×(梯形的面积-半圆的面积),据此解答。
【详解】
[(4+6)×3÷2-×3.14×(4÷2)2]×1200
=[10×3÷2-×3.14×4]×1200
=[15-6.28]×1200
=8.72×1200
=10464(立方米)
答:浇筑这条水渠至少需要混凝土10464立方米。
【点睛】
分析图形求出横截面的面积是解答题目的关键。
答案第1页,共2页
答案第1页,共2页
