【备考2022】泰安市近十年中考数学 考点4 统计与概率-常用统计量(含解析)
文档属性
| 名称 | 【备考2022】泰安市近十年中考数学 考点4 统计与概率-常用统计量(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 234.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 10:04:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
四、统计与概率-常用统计量
[基础知识]
1.统计中的平均数、众数、中位数、极差、方差的概念与计算 ;
2.方差公式:
3.统计量的意义、变化与规律;平均数代表平均水平,中位数代表中间水平,众数代表多数水平,方差、标准差代表数据的稳定性;
4.概率的意义,概率的求法:画树状图或列表法求概率;
注意的问题 :算准事件发生的次数和总次数;②看准是一步还是两步;③第二步是放回还是不放回;
5.用统计与概率的知识解决其他问题。
[中考真题]
(2021)5.(4分)为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,则所调查学生睡眠时间的众数,中位数分别为( )
A.7h,7h B.8h,7.5h C.7h,7.5h D.8h,8h
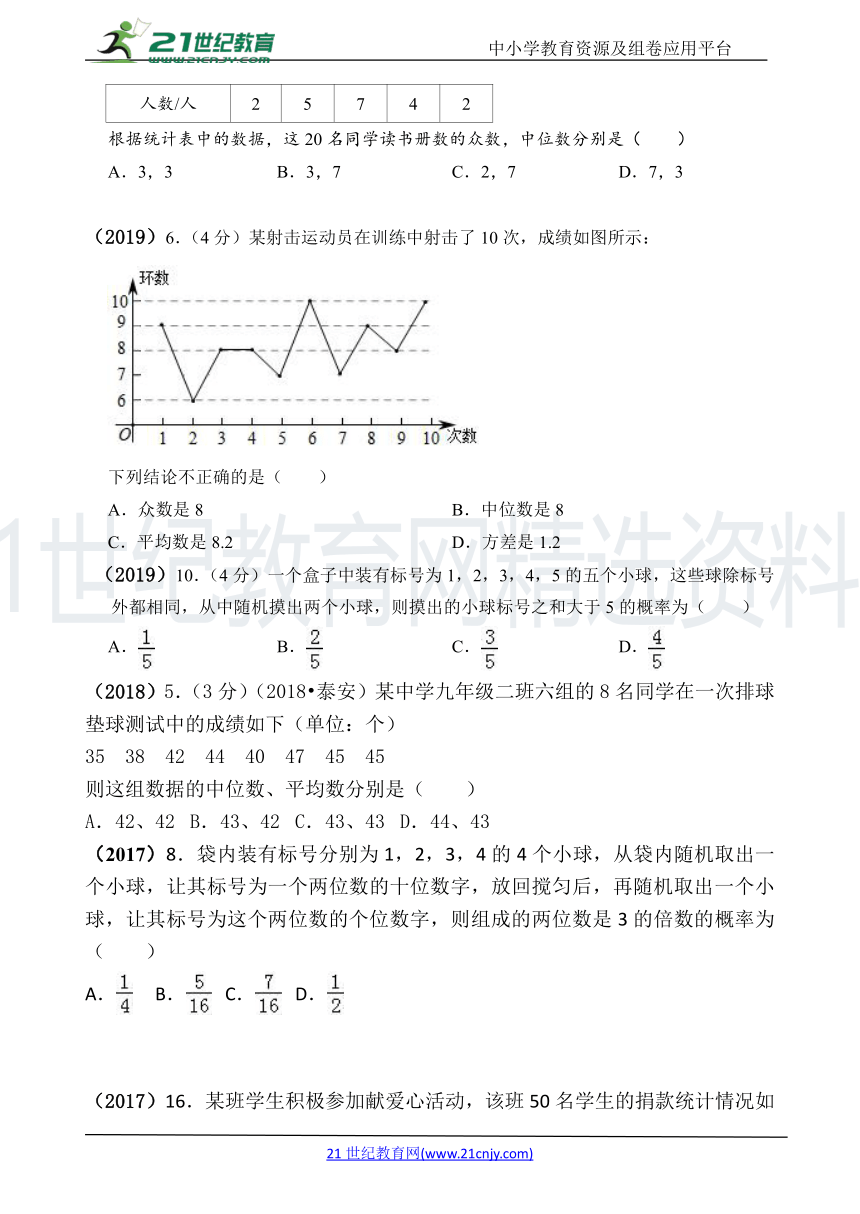
(2020)5.某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:
册数/册 1 2 3 4 5
人数/人 2 5 7 4 2
根据统计表中的数据,这20名同学读书册数的众数,中位数分别是( )
A.3,3 B.3,7 C.2,7 D.7,3
(2019)6.(4分)某射击运动员在训练中射击了10次,成绩如图所示:
下列结论不正确的是( )
A.众数是8 B.中位数是8
C.平均数是8.2 D.方差是1.2
(2019)10.(4分)一个盒子中装有标号为1,2,3,4,5的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球标号之和大于5的概率为( )
A. B. C. D.
(2018)5.(3分)(2018 泰安)某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个)
35 38 42 44 40 47 45 45
则这组数据的中位数、平均数分别是( )
A.42、42 B.43、42 C.43、43 D.44、43
(2017)8.袋内装有标号分别为1,2,3,4的4个小球,从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字,则组成的两位数是3的倍数的概率为( )
A. B. C. D.
(2017)16.某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 5 10 20 50 100
人数 4 16 15 9 6
则他们捐款金额的中位数和平均数分别是( )
A.10,20.6 B.20,20.6 C.10,30.6 D.20,30.6
(2016)3.下列图形:
任取一个是中心对称图形的概率是( )
A. B. C. D.1
(2016)15.(3分)在﹣2,﹣1,0,1,2这五个数中任取两数m,n,则二次函数y=(x﹣m)2+n的顶点在坐标轴上的概率为( )
A. B. C. D.
(2015)6.(3分)如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
(2015)10.(3分)若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上数字为7,则从3、4、5、6、8、9中任选两数,与7组成“中高数”的概率是( )
A. B. C. D.
(2014)9.以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩/分 80 85 90 95
人数/人 1 2 5 2
则这组数据的中位数和平均数分别为( )
A.90,90 B. 90,89 C. 85,89 D. 85,90
(2013)7.实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )
A.4,5 B.5,4 C.4,4 D.5,5
(2013)12.有三张正面分别写有数字﹣1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为( )
(2012)8.某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月约节水情况.见表:
请你估计这400名同学的家庭一个月节约用水的总量大约是( )
A.130m3 B.135m3 C.6.5m3 D.260m3
(2012)15.一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为( )
A. B. C. D.
[答案解析]
(2021)5.(4分)为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,则所调查学生睡眠时间的众数,中位数分别为( )
A.7h,7h B.8h,7.5h C.7h,7.5h D.8h,8h
.
【分析】 根据频数分布直方图确定各小组数量,求出众数、中位数。
【解答】: ∵7h出现了19次,出现的次数最多,
∴所调查学生睡眠时间的众数是7h;
∵共有50名学生,中位数是第25、26个数的平均数,
∴所调查学生睡眠时间的中位数是=7.5(h).
故选:C.
(2020)5.某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:
册数/册 1 2 3 4 5
人数/人 2 5 7 4 2
根据统计表中的数据,这20名同学读书册数的众数,中位数分别是( )
A.3,3 B.3,7 C.2,7 D.7,3
【分析】 找到出现次数最多的数据,即为众数;求出第10、11个数据的平均数即可得这组数据的中位数,从而得出答案.
【解答】:这20名同学读书册数的众数为3册,中位数为=3(册),
故选:A.
(2019)6.(4分)某射击运动员在训练中射击了10次,成绩如图所示:
下列结论不正确的是( )
A.众数是8 B.中位数是8
C.平均数是8.2 D.方差是1.2
【分析】 根据众数、中位数、平均数以及方差的算法进行计算,即可得到不正确的选项.用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果叫方差.
【解答】:由图可得,数据8出现3次,次数最多,所以众数为8,故A选项正确;
10次成绩排序后为:6,7,7,8,8,8,9,9,10,10,所以中位数是(8+8)=8,
故B选项正确;
平均数为(6+7×2+8×3+9×2+10×2)=8.2,故C选项正确;
方差为[(6﹣8.2)2+(7﹣8.2)2+(7﹣8.2)2+(8﹣8.2)2+(8﹣8.2)2+(8﹣8.2)2+(9﹣8.2)2+(9﹣8.2)2+(10﹣8.2)2+(10﹣8.2)2]=1.56,故D选项错误;
故选:D.
(2019)10.(4分)一个盒子中装有标号为1,2,3,4,5的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球标号之和大于5的概率为( )
A. B. C. D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球的标号之和大于5的情况,再利用概率公式即可求得答案.
【解答】解:画树状图如图所示:
∵共有25种等可能的结果,两次摸出的小球的标号之和大于5的有15种结果,
∴两次摸出的小球的标号之和大于5的概率为=;
故选:C.
(2018)5.(3分)(2018 泰安)某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个)
35 38 42 44 40 47 45 45
则这组数据的中位数、平均数分别是( )
A.42、42 B.43、42 C.43、43 D.44、43
【分析】根据中位线的概念求出中位数,利用算术平均数的计算公式求出平均数.
【解答】 把这组数据排列顺序得:35 38 40 42 44 45 45 47,
则这组数据的中位数为:=43,
=(35+38+42+44+40+47+45+45)=42,
故选:B.
(2017)8.袋内装有标号分别为1,2,3,4的4个小球,从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字,则组成的两位数是3的倍数的概率为( )
A. B. C. D.
【分析】画树状图展示所有16种等可能的结果数,再找出所成的两位数是3的倍数的结果数,然后根据概率公式求解.
【解答】:画树状图为:
共有16种等可能的结果数,其中所成的两位数是3的倍数的结果数为5,
所以成的两位数是3的倍数的概率=.
故选B.
(2017)16.某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 5 10 20 50 100
人数 4 16 15 9 6
则他们捐款金额的中位数和平均数分别是( )
A.10,20.6 B.20,20.6 C.10,30.6 D.20,30.6
【分析】根据中位数的定义求解即可,中位数是将一组数据从小到大重新排列后,找出最中间两个数的平均数;根据平均数公式求出平均数即可.
【解答】共有50个数,
∴中位数是第25、26个数的平均数,
∴中位数是(20+20)÷2=20;
平均数=(5×4+10×16+20×15+50×9+100×6)=30.6;
故选:D.
(2016)3.下列图形:
任取一个是中心对称图形的概率是( )
A. B. C. D.1
【分析】由共有4种等可能的结果,任取一个是中心对称图形的有3种情况,直接利用概率公式求解即可求得答案.
【解答】∵共有4种等可能的结果,任取一个是中心对称图形的有3种情况,
∴任取一个是中心对称图形的概率是:.
故选C.
(2016)15.在﹣2,﹣1,0,1,2这五个数中任取两数m,n,则二次函数y=(x﹣m)2+n的顶点在坐标轴上的概率为( )
A. B. C. D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果以及坐标轴上的点的情况,再利用概率公式即可求得答案.
【解答】画树状图得:
∵﹣2,﹣1,0,1,2这五个数中任取两数m,n,一共有20种可能,其中取到0的有8种可能,
∴顶点在坐标轴上的概率为=.
故选A.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比,属于中考常考题型.
(2015)6.(3分) 如图,在方格 ( http: / / www.21cnjy.com )纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
( http: / / www.21cnjy.com )
A. B. C. D.
【分析】由随机选择标有序号 ( http: / / www.21cnjy.com )①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有3种情况,直接利用概率公式求解即可求得答案.
【解答】: ∵在方格纸中,随机选择标有 ( http: / / www.21cnjy.com )序号①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有②④⑤,3种情况,
∴使与图中阴影部分构成轴对称图形的概率是:3÷5=.
故选C.
(2015)10.(3分) 若十位上的数 ( http: / / www.21cnjy.com )字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上数字为7,则从3、4、5、6、8、9中任选两数,与7组成“中高数”的概率是( )
A. B. C. D.
【分析】 首先根据题意列出表格,然后由表格即可求得所有等可能的结果与与7组成“中高数”的情况,再利用概率公式即可求得答案.
【解答】:列表得:
9 379 479 579 679 879 ﹣
8 378 478 578 678 ﹣ 978
6 376 476 576 ﹣ 876 976
5 375 475 ﹣ 675 875 975
4 374 ﹣ 574 674 874 974
3 ﹣ 473 573 673 873 973
3 4 5 6 8 9
∵共有30种等可能的结果,与7组成“中高数”的有12种情况,
∴与7组成“中高数”的概率是:=.
故选C.
点评: 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
(2014)9.以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩/分 80 85 90 95
人数/人 1 2 5 2
则这组数据的中位数和平均数分别为( )
A.90,90 B. 90,89 C. 85,89 D. 85,90
【分析】根据中位数的定义先把这些数从小到大排列,求出最中间的两个数的平均数,再根据平均数的计算公式进行计算即可.
【解答】:∵共有10名同学,中位数是第5和6的平均数,∴这组数据的中位数是(90+90)÷2=90;这组数据的平均数是:(80+85×2+90×5+95×2)÷10=89;故选B.
(2014)11.在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,从中随机摸出一个小球记下标号后放回,再从中随机摸出一个小球,则两次摸出的小球的标号之和大于4的概率是( )
A. B. C. D.
【分析】 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球的标号之和大于4的情况,再利用概率公式即可求得答案.
【解答】:画树状图得:
∵共有16种等可能的结果,两次摸出的小球的标号之和大于4的有10种情况,
∴两次摸出的小球的标号之和大于4的概率是:=.故选C.
(2013)7.实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )
A.4,5 B.5,4 C.4,4 D.5,5
【分析】根据众数及中位数的定义,结合所给数据即可作出判断.
【解答】:将数据从小到大排列为:1,2,3,3,4,4,5,5,5,5,
这组数据的众数为:5;
中位数为:4.
故选A.
(2013)12.有三张正面分别写有数字﹣1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为( )
【分析】画出树状图,然后确定出在第二象限的点的个数,再根据概率公式列式进行计算即可得解.
【解答】:根据题意,画出树状图如下:
一共有6种情况,在第二象限的点有(﹣1,1)(﹣1,2)共2个,
所以,P==.
故选B.
(2012)8.某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月约节水情况.见表:
请你估计这400名同学的家庭一个月节约用水的总量大约是( )
A.130m3 B.135m3 C.6.5m3 D.260m3
【分析】用样本估计总体;加权平均数。
【解答】: 20名同学各自家庭一个月平均节约用水是:
(0.2×2+0.25×4+0.3×6+04×7+0.5×1)÷20=0.325(m3),
因此这400名同学的家庭一个月节约用水的总量大约是:
400×0.325=130(m3),
故选A.
(2012)15.一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为( )
A. B. C. D.
【分析】列表法与树状图法。
【解答】:列表得:
∵共有12种等可能的结果,这两个乒乓球上的数字之和大于5的有4种情况,
∴这两个乒乓球上的数字之和大于5的概率为:.
故选B.
[解题攻略]
掌握统计与概率的相关概念、理解其意义和计算公式是解题的关键。中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,概率=所求情况数与总情况数之比.
.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
四、统计与概率-常用统计量
[基础知识]
1.统计中的平均数、众数、中位数、极差、方差的概念与计算 ;
2.方差公式:
3.统计量的意义、变化与规律;平均数代表平均水平,中位数代表中间水平,众数代表多数水平,方差、标准差代表数据的稳定性;
4.概率的意义,概率的求法:画树状图或列表法求概率;
注意的问题 :算准事件发生的次数和总次数;②看准是一步还是两步;③第二步是放回还是不放回;
5.用统计与概率的知识解决其他问题。
[中考真题]
(2021)5.(4分)为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,则所调查学生睡眠时间的众数,中位数分别为( )
A.7h,7h B.8h,7.5h C.7h,7.5h D.8h,8h
(2020)5.某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:
册数/册 1 2 3 4 5
人数/人 2 5 7 4 2
根据统计表中的数据,这20名同学读书册数的众数,中位数分别是( )
A.3,3 B.3,7 C.2,7 D.7,3
(2019)6.(4分)某射击运动员在训练中射击了10次,成绩如图所示:
下列结论不正确的是( )
A.众数是8 B.中位数是8
C.平均数是8.2 D.方差是1.2
(2019)10.(4分)一个盒子中装有标号为1,2,3,4,5的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球标号之和大于5的概率为( )
A. B. C. D.
(2018)5.(3分)(2018 泰安)某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个)
35 38 42 44 40 47 45 45
则这组数据的中位数、平均数分别是( )
A.42、42 B.43、42 C.43、43 D.44、43
(2017)8.袋内装有标号分别为1,2,3,4的4个小球,从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字,则组成的两位数是3的倍数的概率为( )
A. B. C. D.
(2017)16.某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 5 10 20 50 100
人数 4 16 15 9 6
则他们捐款金额的中位数和平均数分别是( )
A.10,20.6 B.20,20.6 C.10,30.6 D.20,30.6
(2016)3.下列图形:
任取一个是中心对称图形的概率是( )
A. B. C. D.1
(2016)15.(3分)在﹣2,﹣1,0,1,2这五个数中任取两数m,n,则二次函数y=(x﹣m)2+n的顶点在坐标轴上的概率为( )
A. B. C. D.
(2015)6.(3分)如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
(2015)10.(3分)若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上数字为7,则从3、4、5、6、8、9中任选两数,与7组成“中高数”的概率是( )
A. B. C. D.
(2014)9.以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩/分 80 85 90 95
人数/人 1 2 5 2
则这组数据的中位数和平均数分别为( )
A.90,90 B. 90,89 C. 85,89 D. 85,90
(2013)7.实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )
A.4,5 B.5,4 C.4,4 D.5,5
(2013)12.有三张正面分别写有数字﹣1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为( )
(2012)8.某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月约节水情况.见表:
请你估计这400名同学的家庭一个月节约用水的总量大约是( )
A.130m3 B.135m3 C.6.5m3 D.260m3
(2012)15.一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为( )
A. B. C. D.
[答案解析]
(2021)5.(4分)为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,则所调查学生睡眠时间的众数,中位数分别为( )
A.7h,7h B.8h,7.5h C.7h,7.5h D.8h,8h
.
【分析】 根据频数分布直方图确定各小组数量,求出众数、中位数。
【解答】: ∵7h出现了19次,出现的次数最多,
∴所调查学生睡眠时间的众数是7h;
∵共有50名学生,中位数是第25、26个数的平均数,
∴所调查学生睡眠时间的中位数是=7.5(h).
故选:C.
(2020)5.某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:
册数/册 1 2 3 4 5
人数/人 2 5 7 4 2
根据统计表中的数据,这20名同学读书册数的众数,中位数分别是( )
A.3,3 B.3,7 C.2,7 D.7,3
【分析】 找到出现次数最多的数据,即为众数;求出第10、11个数据的平均数即可得这组数据的中位数,从而得出答案.
【解答】:这20名同学读书册数的众数为3册,中位数为=3(册),
故选:A.
(2019)6.(4分)某射击运动员在训练中射击了10次,成绩如图所示:
下列结论不正确的是( )
A.众数是8 B.中位数是8
C.平均数是8.2 D.方差是1.2
【分析】 根据众数、中位数、平均数以及方差的算法进行计算,即可得到不正确的选项.用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果叫方差.
【解答】:由图可得,数据8出现3次,次数最多,所以众数为8,故A选项正确;
10次成绩排序后为:6,7,7,8,8,8,9,9,10,10,所以中位数是(8+8)=8,
故B选项正确;
平均数为(6+7×2+8×3+9×2+10×2)=8.2,故C选项正确;
方差为[(6﹣8.2)2+(7﹣8.2)2+(7﹣8.2)2+(8﹣8.2)2+(8﹣8.2)2+(8﹣8.2)2+(9﹣8.2)2+(9﹣8.2)2+(10﹣8.2)2+(10﹣8.2)2]=1.56,故D选项错误;
故选:D.
(2019)10.(4分)一个盒子中装有标号为1,2,3,4,5的五个小球,这些球除标号外都相同,从中随机摸出两个小球,则摸出的小球标号之和大于5的概率为( )
A. B. C. D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球的标号之和大于5的情况,再利用概率公式即可求得答案.
【解答】解:画树状图如图所示:
∵共有25种等可能的结果,两次摸出的小球的标号之和大于5的有15种结果,
∴两次摸出的小球的标号之和大于5的概率为=;
故选:C.
(2018)5.(3分)(2018 泰安)某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个)
35 38 42 44 40 47 45 45
则这组数据的中位数、平均数分别是( )
A.42、42 B.43、42 C.43、43 D.44、43
【分析】根据中位线的概念求出中位数,利用算术平均数的计算公式求出平均数.
【解答】 把这组数据排列顺序得:35 38 40 42 44 45 45 47,
则这组数据的中位数为:=43,
=(35+38+42+44+40+47+45+45)=42,
故选:B.
(2017)8.袋内装有标号分别为1,2,3,4的4个小球,从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字,则组成的两位数是3的倍数的概率为( )
A. B. C. D.
【分析】画树状图展示所有16种等可能的结果数,再找出所成的两位数是3的倍数的结果数,然后根据概率公式求解.
【解答】:画树状图为:
共有16种等可能的结果数,其中所成的两位数是3的倍数的结果数为5,
所以成的两位数是3的倍数的概率=.
故选B.
(2017)16.某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 5 10 20 50 100
人数 4 16 15 9 6
则他们捐款金额的中位数和平均数分别是( )
A.10,20.6 B.20,20.6 C.10,30.6 D.20,30.6
【分析】根据中位数的定义求解即可,中位数是将一组数据从小到大重新排列后,找出最中间两个数的平均数;根据平均数公式求出平均数即可.
【解答】共有50个数,
∴中位数是第25、26个数的平均数,
∴中位数是(20+20)÷2=20;
平均数=(5×4+10×16+20×15+50×9+100×6)=30.6;
故选:D.
(2016)3.下列图形:
任取一个是中心对称图形的概率是( )
A. B. C. D.1
【分析】由共有4种等可能的结果,任取一个是中心对称图形的有3种情况,直接利用概率公式求解即可求得答案.
【解答】∵共有4种等可能的结果,任取一个是中心对称图形的有3种情况,
∴任取一个是中心对称图形的概率是:.
故选C.
(2016)15.在﹣2,﹣1,0,1,2这五个数中任取两数m,n,则二次函数y=(x﹣m)2+n的顶点在坐标轴上的概率为( )
A. B. C. D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果以及坐标轴上的点的情况,再利用概率公式即可求得答案.
【解答】画树状图得:
∵﹣2,﹣1,0,1,2这五个数中任取两数m,n,一共有20种可能,其中取到0的有8种可能,
∴顶点在坐标轴上的概率为=.
故选A.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比,属于中考常考题型.
(2015)6.(3分) 如图,在方格 ( http: / / www.21cnjy.com )纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
( http: / / www.21cnjy.com )
A. B. C. D.
【分析】由随机选择标有序号 ( http: / / www.21cnjy.com )①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有3种情况,直接利用概率公式求解即可求得答案.
【解答】: ∵在方格纸中,随机选择标有 ( http: / / www.21cnjy.com )序号①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有②④⑤,3种情况,
∴使与图中阴影部分构成轴对称图形的概率是:3÷5=.
故选C.
(2015)10.(3分) 若十位上的数 ( http: / / www.21cnjy.com )字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上数字为7,则从3、4、5、6、8、9中任选两数,与7组成“中高数”的概率是( )
A. B. C. D.
【分析】 首先根据题意列出表格,然后由表格即可求得所有等可能的结果与与7组成“中高数”的情况,再利用概率公式即可求得答案.
【解答】:列表得:
9 379 479 579 679 879 ﹣
8 378 478 578 678 ﹣ 978
6 376 476 576 ﹣ 876 976
5 375 475 ﹣ 675 875 975
4 374 ﹣ 574 674 874 974
3 ﹣ 473 573 673 873 973
3 4 5 6 8 9
∵共有30种等可能的结果,与7组成“中高数”的有12种情况,
∴与7组成“中高数”的概率是:=.
故选C.
点评: 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
(2014)9.以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩/分 80 85 90 95
人数/人 1 2 5 2
则这组数据的中位数和平均数分别为( )
A.90,90 B. 90,89 C. 85,89 D. 85,90
【分析】根据中位数的定义先把这些数从小到大排列,求出最中间的两个数的平均数,再根据平均数的计算公式进行计算即可.
【解答】:∵共有10名同学,中位数是第5和6的平均数,∴这组数据的中位数是(90+90)÷2=90;这组数据的平均数是:(80+85×2+90×5+95×2)÷10=89;故选B.
(2014)11.在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,从中随机摸出一个小球记下标号后放回,再从中随机摸出一个小球,则两次摸出的小球的标号之和大于4的概率是( )
A. B. C. D.
【分析】 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球的标号之和大于4的情况,再利用概率公式即可求得答案.
【解答】:画树状图得:
∵共有16种等可能的结果,两次摸出的小球的标号之和大于4的有10种情况,
∴两次摸出的小球的标号之和大于4的概率是:=.故选C.
(2013)7.实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )
A.4,5 B.5,4 C.4,4 D.5,5
【分析】根据众数及中位数的定义,结合所给数据即可作出判断.
【解答】:将数据从小到大排列为:1,2,3,3,4,4,5,5,5,5,
这组数据的众数为:5;
中位数为:4.
故选A.
(2013)12.有三张正面分别写有数字﹣1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为( )
【分析】画出树状图,然后确定出在第二象限的点的个数,再根据概率公式列式进行计算即可得解.
【解答】:根据题意,画出树状图如下:
一共有6种情况,在第二象限的点有(﹣1,1)(﹣1,2)共2个,
所以,P==.
故选B.
(2012)8.某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月约节水情况.见表:
请你估计这400名同学的家庭一个月节约用水的总量大约是( )
A.130m3 B.135m3 C.6.5m3 D.260m3
【分析】用样本估计总体;加权平均数。
【解答】: 20名同学各自家庭一个月平均节约用水是:
(0.2×2+0.25×4+0.3×6+04×7+0.5×1)÷20=0.325(m3),
因此这400名同学的家庭一个月节约用水的总量大约是:
400×0.325=130(m3),
故选A.
(2012)15.一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为( )
A. B. C. D.
【分析】列表法与树状图法。
【解答】:列表得:
∵共有12种等可能的结果,这两个乒乓球上的数字之和大于5的有4种情况,
∴这两个乒乓球上的数字之和大于5的概率为:.
故选B.
[解题攻略]
掌握统计与概率的相关概念、理解其意义和计算公式是解题的关键。中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,概率=所求情况数与总情况数之比.
.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
