【备考2022】泰安市近十年中考数学 考点5 统计与概率-统计图表(含解析)
文档属性
| 名称 | 【备考2022】泰安市近十年中考数学 考点5 统计与概率-统计图表(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 341.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
统计与概率-统计图表
[基础知识]
统计图表:扇形统计图、条形统计图、拆线统计图;
频率=频数/总数;
扇形圆心角度数=360°×各小组频率;
条形统计图各小组频数之和等于数据总数;
概率的计算:画树状图、列表法;
用样本估计总体。
[中考真题]
(2021)20.(10分)为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息,解答下列问题:
(1)本次共调查了 名学生;C组所在扇形的圆心角为 度;
(2)该校共有学生1600人,若90分以上为优秀,估计该校优秀学生人数为多少?
(3)若E组14名学生中有4人满分,设这4名学生为E1,E2,E3,E4,从其中抽取2名学生代表学校参加上一级比赛,请用列表或画树状图的方法求恰好抽到E1,E2的概率.
竞赛成绩统计表(成绩满分100分)
组别 分数 人数
A组 75<x≤80 4
B组 80<x≤85
C组 85<x≤90 10
D组 90<x≤95
E组 95<x≤100 14
合计
(2020)21.为迎接2020年第35届全国青少年科技创新大赛,某学校举办了A:机器人;B:航模;C:科幻绘画;D:信息学;E:科技小制作等五项比赛活动(每人限报一项),将各项比赛的参加人数绘制成如图两幅不完整的统计图.
根据统计图中的信息解答下列问题:
(1)本次参加比赛的学生人数是 名;
(2)把条形统计图补充完整;
(3)求扇形统计图中表示机器人的扇形圆心角α的度数;
(4)在C组最优秀的3名同学(1名男生2名女生)和E组最优秀的3名同学(2名男生1名女生)中,各选1名同学参加上一级比赛,利用树状图或表格,求所选两名同学中恰好是1名男生1名女生的概率.
(2019)20.(8分)为弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 分数 人数
第1组 90<x≤100 8
第2组 80<x≤90 a
第3组 70<x≤80 10
第4组 60<x≤70 b
第5组 50<x≤60 3
请根据以上信息,解答下列问题:
(1)求出a,b的值;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?
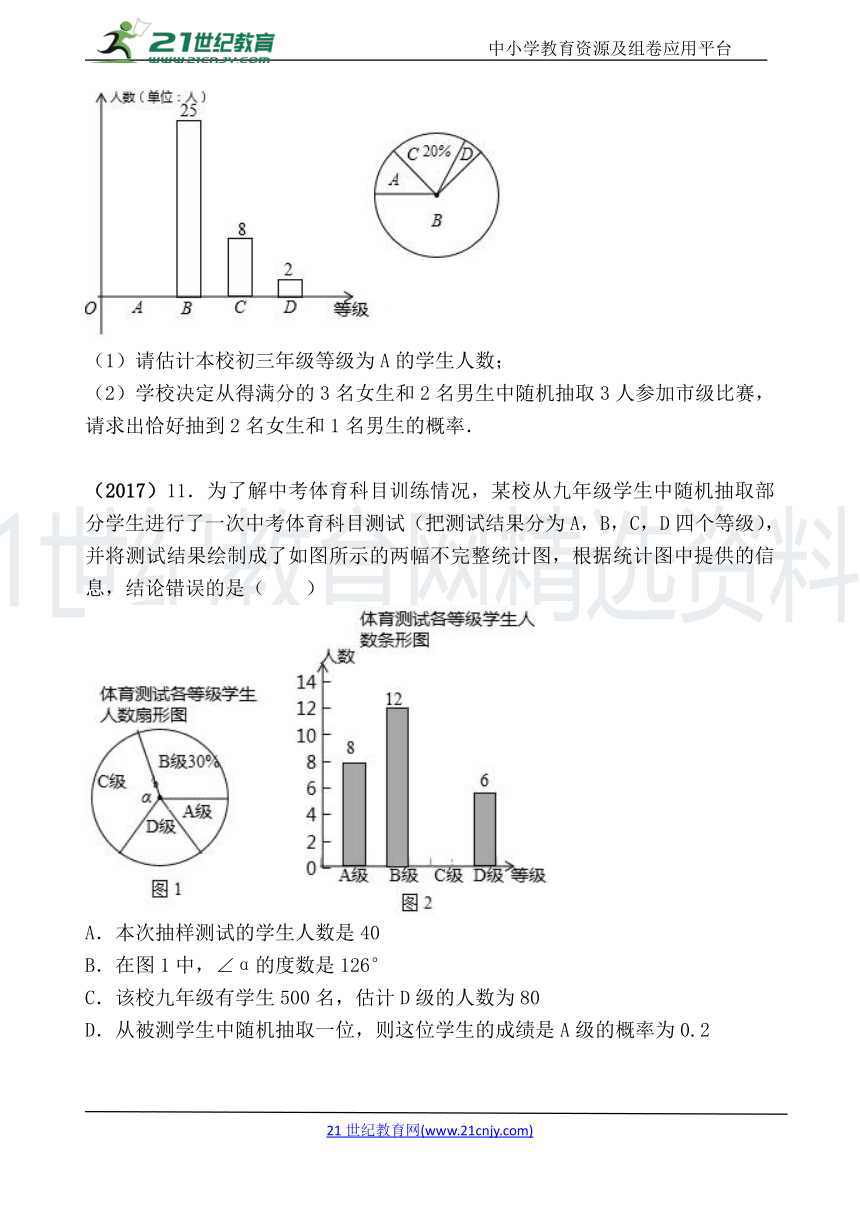
(2018)21.(8分)为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取一个班学生的成绩进行整理,分为A,B,C,D四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)请估计本校初三年级等级为A的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.
(2017)11.为了解中考体育科目训练情况,某校从九年级学生中随机抽取部分学生进行了一次中考体育科目测试(把测试结果分为A,B,C,D四个等级),并将测试结果绘制成了如图所示的两幅不完整统计图,根据统计图中提供的信息,结论错误的是( )
A.本次抽样测试的学生人数是40
B.在图1中,∠α的度数是126°
C.该校九年级有学生500名,估计D级的人数为80
D.从被测学生中随机抽取一位,则这位学生的成绩是A级的概率为0.2
(2016)11.某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
选修课 A B C D E F
人数 40 60 100
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E、F的人数分别为80,70
D.喜欢选修课C的人数最少
(2015)11.(3分) 某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
( http: / / www.21cnjy.com )
A.94分,96分 B. 96分,96分 C. 94分,96.4分 D. 96分,96.4分
(2014)22.七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用水量x/m3 0<x≤5 5<x≤10 10<x≤15 15<x≤20 x>20
频数/户 12 20 3
频率 0.12 0.07
若该小区有800户家庭,据此估计该小区月均用水量不超过10m3的家庭约有 户.
[答案解析]
(2021)20.(10分)为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息,解答下列问题:
(1)本次共调查了 名学生;C组所在扇形的圆心角为 度;
(2)该校共有学生1600人,若90分以上为优秀,估计该校优秀学生人数为多少?
(3)若E组14名学生中有4人满分,设这4名学生为E1,E2,E3,E4,从其中抽取2名学生代表学校参加上一级比赛,请用列表或画树状图的方法求恰好抽到E1,E2的概率.
竞赛成绩统计表(成绩满分100分)
组别 分数 人数
A组 75<x≤80 4
B组 80<x≤85
C组 85<x≤90 10
D组 90<x≤95
E组 95<x≤100 14
合计
【分析】
【解答】(1)本次共调查的学生=14÷28%=50(人);
C组的圆心角为360°×=72°,
故答案为50;72;
(2)B组的人数为50×12%=16(人),
则D组的人数为50﹣4﹣6﹣1﹣14=16(人),
则优秀的人数为1600×=960(人);
(3)画树状图为:
共有12种等可能的结果,其中恰好抽到E1,E2的结果数为2,
所以恰好抽到E1,E2的概率==.
(2020)21.为迎接2020年第35届全国青少年科技创新大赛,某学校举办了A:机器人;B:航模;C:科幻绘画;D:信息学;E:科技小制作等五项比赛活动(每人限报一项),将各项比赛的参加人数绘制成如图两幅不完整的统计图.
根据统计图中的信息解答下列问题:
(1)本次参加比赛的学生人数是 80 名;
(2)把条形统计图补充完整;
(3)求扇形统计图中表示机器人的扇形圆心角α的度数;
(4)在C组最优秀的3名同学(1名男生2名女生)和E组最优秀的3名同学(2名男生1名女生)中,各选1名同学参加上一级比赛,利用树状图或表格,求所选两名同学中恰好是1名男生1名女生的概率.
【分析】 (1)由B组的人数及其所占百分比可得本次参加比赛的学生人数;
(2)求出D组人数,从而补全条形统计图;
(3)由360°乘以A组所占的百分比即可;
(4)画出树状图,由概率公式求解即可.
【解答】: (1)本次参加比赛的学生人数为18÷22.5%=80(名);
故答案为:80;
(2)D组人数为:80﹣16﹣18﹣20﹣8=18(名),把条形统计图补充完整如图:
(3)扇形统计图中表示机器人的扇形圆心角α的度数为360°×=72°;
(4)画树状图如图:
共有9个等可能的结果,所选两名同学中恰好是1名男生1名女生的结果有5个,
∴所选两名同学中恰好是1名男生1名女生的概率为.
(2019)20.(8分)为弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 分数 人数
第1组 90<x≤100 8
第2组 80<x≤90 a
第3组 70<x≤80 10
第4组 60<x≤70 b
第5组 50<x≤60 3
请根据以上信息,解答下列问题:
(1)求出a,b的值;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?
【分析】 (1)抽取学生人数10÷25%=40(人),第2组人数 40×50%﹣8=12(人),第4组人数 40×50%﹣10﹣3=7(人),所以a=12,b=7;
(2)=27°,所以“第5组”所在扇形圆心角的度数为27°;
(3)成绩高于80分:1800×50%=900(人),所以成绩高于80分的共有900人.
【解答】:(1)抽取学生人数10÷25%=40(人),
第2组人数 40×50%﹣8=12(人),
第4组人数 40×50%﹣10﹣3=7(人),
∴a=12,b=7;
(2)=27°,
∴“第5组”所在扇形圆心角的度数为27°;
(3)成绩高于80分:1800×50%=900(人),
∴成绩高于80分的共有900人.
(2018)21.(8分)为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取一个班学生的成绩进行整理,分为A,B,C,D四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)请估计本校初三年级等级为A的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.
【分析】 1)先根据C等级人数及其所占百分比求得总人数,用总人数减去B、C、D的人数求得A等级人数,再用总人数乘以样本中A等级人数所占比例;
(2)列出从3名女生和2名男生中随机抽取3人的所有等可能结果,再从中找到恰好抽到2名女生和1名男生的结果数,根据概率公式计算可得.
【解答】(1)∵所抽取学生的总数为8÷20%=40人,
∴该班级等级为A的学生人数为40﹣(25+8+2)=5人,
则估计本校初三年级等级为A的学生人数为1000×=125人;
(2)设两位满分的男生记为A1、A2、三位满分的女生记为B1、B2、B3,
从这5名同学中选3人的所有等可能结果为:
(B1,B2,B3)、(A2,B2,B3)、(A2,B1,B3)、(A2,B1,B2)、(A1,B2,B3)、
(A1,B1,B3)、(A1,B1,B2)、(A1,A2,B3)、(A1,A2,B2)、(A1,A2,B1),
其中恰好有2名女生、1名男生的结果有6种,
所以恰好抽到2名女生和1名男生的概率为=.
(2017)11.为了解中考体育科目训练情况,某校从九年级学生中随机抽取部分学生进行了一次中考体育科目测试(把测试结果分为A,B,C,D四个等级),并将测试结果绘制成了如图所示的两幅不完整统计图,根据统计图中提供的信息,结论错误的是( )
A.本次抽样测试的学生人数是40
B.在图1中,∠α的度数是126°
C.该校九年级有学生500名,估计D级的人数为80
D.从被测学生中随机抽取一位,则这位学生的成绩是A级的概率为0.2
【分析】 利用扇形统计图以及条形统计图分别分析得出总人数以及结合α的度数、利用样本估计总体即可.
【解答】:A、本次抽样测试的学生人数是:12÷30%=40(人),正确,不合题意;
B、∵×360°=126°,∠α的度数是126°,故此选项正确,不合题意;
C、该校九年级有学生500名,估计D级的人数为:500×=100(人),故此选项错误,符合题意;
D、从被测学生中随机抽取一位,则这位学生的成绩是A级的概率为: =0.2,正确,不合题意;
故选:C.
(2016)11.某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
选修课 A B C D E F
人数 40 60 100
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E、F的人数分别为80,70
D.喜欢选修课C的人数最少
【分析】通过计算得出选项A、B、C正确,选项D错误,即可得出结论.
【解答】被调查的学生人数为60÷15%=400(人),
∴选项A正确;
扇形统计图中D的圆心角为×360°=90°,
∵×360°=36°,360°(17.5%+15%+12.5%)=162°,
∴扇形统计图中E的圆心角=360°﹣162°﹣90°﹣36°=72°,
∴选项B正确;
∵400×=80(人),400×17.5%=70(人),
∴选项C正确;
∵12.5%>10%,
∴喜欢选修课A的人数最少,
∴选项D错误;
故选:D.
【点评】本题考查了条形统计图、扇形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
(2015)11.(3分) 某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )21教育网
( http: / / www.21cnjy.com )
A.94分,96分 B. 96分,96分 C. 94分,96.4分 D. 96分,96.4分
【分析】 首先利用扇形图以 ( http: / / www.21cnjy.com )及条形图求出总人数,进而求得每个小组的人数,然后根据中位数的定义求出这些职工成绩的中位数,利用加权平均数公式求出这些职工成绩的平均数.
【解答】: 总人数为6÷10%=60(人),
则94分的有60×20%=12(人),
98分的有60﹣6﹣12﹣15﹣9=18(人),
第30与31个数据都是96分,这些职工成绩的中位数是(96+96)÷2=96;
这些职工成绩的平均数是(92×6+94×12+96×15+98×18+100×9)÷60
=(552+1128+1440+1764+900)÷60
=5784÷60
=96.4.
故选:D.
(2014)22.七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用水量x/m3 0<x≤5 5<x≤10 10<x≤15 15<x≤20 x>20
频数/户 12 20 3
频率 0.12 0.07
若该小区有800户家庭,据此估计该小区月均用水量不超过10m3的家庭约有 户.
【分析】 根据=总数之间的关系求出5<x≤10的频数,再用整体×样本的百分比即可得出答案.
【解答】:根据题意得:=100(户),15<x≤20的频数是0.07×100=7(户),
5<x≤10的频数是:100﹣12﹣20﹣7﹣3=58(户),
则该小区月均用水量不超过10m3的家庭约有×800=560(户);故答案为:560.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
统计与概率-统计图表
[基础知识]
统计图表:扇形统计图、条形统计图、拆线统计图;
频率=频数/总数;
扇形圆心角度数=360°×各小组频率;
条形统计图各小组频数之和等于数据总数;
概率的计算:画树状图、列表法;
用样本估计总体。
[中考真题]
(2021)20.(10分)为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息,解答下列问题:
(1)本次共调查了 名学生;C组所在扇形的圆心角为 度;
(2)该校共有学生1600人,若90分以上为优秀,估计该校优秀学生人数为多少?
(3)若E组14名学生中有4人满分,设这4名学生为E1,E2,E3,E4,从其中抽取2名学生代表学校参加上一级比赛,请用列表或画树状图的方法求恰好抽到E1,E2的概率.
竞赛成绩统计表(成绩满分100分)
组别 分数 人数
A组 75<x≤80 4
B组 80<x≤85
C组 85<x≤90 10
D组 90<x≤95
E组 95<x≤100 14
合计
(2020)21.为迎接2020年第35届全国青少年科技创新大赛,某学校举办了A:机器人;B:航模;C:科幻绘画;D:信息学;E:科技小制作等五项比赛活动(每人限报一项),将各项比赛的参加人数绘制成如图两幅不完整的统计图.
根据统计图中的信息解答下列问题:
(1)本次参加比赛的学生人数是 名;
(2)把条形统计图补充完整;
(3)求扇形统计图中表示机器人的扇形圆心角α的度数;
(4)在C组最优秀的3名同学(1名男生2名女生)和E组最优秀的3名同学(2名男生1名女生)中,各选1名同学参加上一级比赛,利用树状图或表格,求所选两名同学中恰好是1名男生1名女生的概率.
(2019)20.(8分)为弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 分数 人数
第1组 90<x≤100 8
第2组 80<x≤90 a
第3组 70<x≤80 10
第4组 60<x≤70 b
第5组 50<x≤60 3
请根据以上信息,解答下列问题:
(1)求出a,b的值;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?
(2018)21.(8分)为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取一个班学生的成绩进行整理,分为A,B,C,D四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)请估计本校初三年级等级为A的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.
(2017)11.为了解中考体育科目训练情况,某校从九年级学生中随机抽取部分学生进行了一次中考体育科目测试(把测试结果分为A,B,C,D四个等级),并将测试结果绘制成了如图所示的两幅不完整统计图,根据统计图中提供的信息,结论错误的是( )
A.本次抽样测试的学生人数是40
B.在图1中,∠α的度数是126°
C.该校九年级有学生500名,估计D级的人数为80
D.从被测学生中随机抽取一位,则这位学生的成绩是A级的概率为0.2
(2016)11.某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
选修课 A B C D E F
人数 40 60 100
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E、F的人数分别为80,70
D.喜欢选修课C的人数最少
(2015)11.(3分) 某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
( http: / / www.21cnjy.com )
A.94分,96分 B. 96分,96分 C. 94分,96.4分 D. 96分,96.4分
(2014)22.七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用水量x/m3 0<x≤5 5<x≤10 10<x≤15 15<x≤20 x>20
频数/户 12 20 3
频率 0.12 0.07
若该小区有800户家庭,据此估计该小区月均用水量不超过10m3的家庭约有 户.
[答案解析]
(2021)20.(10分)为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息,解答下列问题:
(1)本次共调查了 名学生;C组所在扇形的圆心角为 度;
(2)该校共有学生1600人,若90分以上为优秀,估计该校优秀学生人数为多少?
(3)若E组14名学生中有4人满分,设这4名学生为E1,E2,E3,E4,从其中抽取2名学生代表学校参加上一级比赛,请用列表或画树状图的方法求恰好抽到E1,E2的概率.
竞赛成绩统计表(成绩满分100分)
组别 分数 人数
A组 75<x≤80 4
B组 80<x≤85
C组 85<x≤90 10
D组 90<x≤95
E组 95<x≤100 14
合计
【分析】
【解答】(1)本次共调查的学生=14÷28%=50(人);
C组的圆心角为360°×=72°,
故答案为50;72;
(2)B组的人数为50×12%=16(人),
则D组的人数为50﹣4﹣6﹣1﹣14=16(人),
则优秀的人数为1600×=960(人);
(3)画树状图为:
共有12种等可能的结果,其中恰好抽到E1,E2的结果数为2,
所以恰好抽到E1,E2的概率==.
(2020)21.为迎接2020年第35届全国青少年科技创新大赛,某学校举办了A:机器人;B:航模;C:科幻绘画;D:信息学;E:科技小制作等五项比赛活动(每人限报一项),将各项比赛的参加人数绘制成如图两幅不完整的统计图.
根据统计图中的信息解答下列问题:
(1)本次参加比赛的学生人数是 80 名;
(2)把条形统计图补充完整;
(3)求扇形统计图中表示机器人的扇形圆心角α的度数;
(4)在C组最优秀的3名同学(1名男生2名女生)和E组最优秀的3名同学(2名男生1名女生)中,各选1名同学参加上一级比赛,利用树状图或表格,求所选两名同学中恰好是1名男生1名女生的概率.
【分析】 (1)由B组的人数及其所占百分比可得本次参加比赛的学生人数;
(2)求出D组人数,从而补全条形统计图;
(3)由360°乘以A组所占的百分比即可;
(4)画出树状图,由概率公式求解即可.
【解答】: (1)本次参加比赛的学生人数为18÷22.5%=80(名);
故答案为:80;
(2)D组人数为:80﹣16﹣18﹣20﹣8=18(名),把条形统计图补充完整如图:
(3)扇形统计图中表示机器人的扇形圆心角α的度数为360°×=72°;
(4)画树状图如图:
共有9个等可能的结果,所选两名同学中恰好是1名男生1名女生的结果有5个,
∴所选两名同学中恰好是1名男生1名女生的概率为.
(2019)20.(8分)为弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 分数 人数
第1组 90<x≤100 8
第2组 80<x≤90 a
第3组 70<x≤80 10
第4组 60<x≤70 b
第5组 50<x≤60 3
请根据以上信息,解答下列问题:
(1)求出a,b的值;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?
【分析】 (1)抽取学生人数10÷25%=40(人),第2组人数 40×50%﹣8=12(人),第4组人数 40×50%﹣10﹣3=7(人),所以a=12,b=7;
(2)=27°,所以“第5组”所在扇形圆心角的度数为27°;
(3)成绩高于80分:1800×50%=900(人),所以成绩高于80分的共有900人.
【解答】:(1)抽取学生人数10÷25%=40(人),
第2组人数 40×50%﹣8=12(人),
第4组人数 40×50%﹣10﹣3=7(人),
∴a=12,b=7;
(2)=27°,
∴“第5组”所在扇形圆心角的度数为27°;
(3)成绩高于80分:1800×50%=900(人),
∴成绩高于80分的共有900人.
(2018)21.(8分)为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取一个班学生的成绩进行整理,分为A,B,C,D四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)请估计本校初三年级等级为A的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.
【分析】 1)先根据C等级人数及其所占百分比求得总人数,用总人数减去B、C、D的人数求得A等级人数,再用总人数乘以样本中A等级人数所占比例;
(2)列出从3名女生和2名男生中随机抽取3人的所有等可能结果,再从中找到恰好抽到2名女生和1名男生的结果数,根据概率公式计算可得.
【解答】(1)∵所抽取学生的总数为8÷20%=40人,
∴该班级等级为A的学生人数为40﹣(25+8+2)=5人,
则估计本校初三年级等级为A的学生人数为1000×=125人;
(2)设两位满分的男生记为A1、A2、三位满分的女生记为B1、B2、B3,
从这5名同学中选3人的所有等可能结果为:
(B1,B2,B3)、(A2,B2,B3)、(A2,B1,B3)、(A2,B1,B2)、(A1,B2,B3)、
(A1,B1,B3)、(A1,B1,B2)、(A1,A2,B3)、(A1,A2,B2)、(A1,A2,B1),
其中恰好有2名女生、1名男生的结果有6种,
所以恰好抽到2名女生和1名男生的概率为=.
(2017)11.为了解中考体育科目训练情况,某校从九年级学生中随机抽取部分学生进行了一次中考体育科目测试(把测试结果分为A,B,C,D四个等级),并将测试结果绘制成了如图所示的两幅不完整统计图,根据统计图中提供的信息,结论错误的是( )
A.本次抽样测试的学生人数是40
B.在图1中,∠α的度数是126°
C.该校九年级有学生500名,估计D级的人数为80
D.从被测学生中随机抽取一位,则这位学生的成绩是A级的概率为0.2
【分析】 利用扇形统计图以及条形统计图分别分析得出总人数以及结合α的度数、利用样本估计总体即可.
【解答】:A、本次抽样测试的学生人数是:12÷30%=40(人),正确,不合题意;
B、∵×360°=126°,∠α的度数是126°,故此选项正确,不合题意;
C、该校九年级有学生500名,估计D级的人数为:500×=100(人),故此选项错误,符合题意;
D、从被测学生中随机抽取一位,则这位学生的成绩是A级的概率为: =0.2,正确,不合题意;
故选:C.
(2016)11.某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
选修课 A B C D E F
人数 40 60 100
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E、F的人数分别为80,70
D.喜欢选修课C的人数最少
【分析】通过计算得出选项A、B、C正确,选项D错误,即可得出结论.
【解答】被调查的学生人数为60÷15%=400(人),
∴选项A正确;
扇形统计图中D的圆心角为×360°=90°,
∵×360°=36°,360°(17.5%+15%+12.5%)=162°,
∴扇形统计图中E的圆心角=360°﹣162°﹣90°﹣36°=72°,
∴选项B正确;
∵400×=80(人),400×17.5%=70(人),
∴选项C正确;
∵12.5%>10%,
∴喜欢选修课A的人数最少,
∴选项D错误;
故选:D.
【点评】本题考查了条形统计图、扇形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
(2015)11.(3分) 某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )21教育网
( http: / / www.21cnjy.com )
A.94分,96分 B. 96分,96分 C. 94分,96.4分 D. 96分,96.4分
【分析】 首先利用扇形图以 ( http: / / www.21cnjy.com )及条形图求出总人数,进而求得每个小组的人数,然后根据中位数的定义求出这些职工成绩的中位数,利用加权平均数公式求出这些职工成绩的平均数.
【解答】: 总人数为6÷10%=60(人),
则94分的有60×20%=12(人),
98分的有60﹣6﹣12﹣15﹣9=18(人),
第30与31个数据都是96分,这些职工成绩的中位数是(96+96)÷2=96;
这些职工成绩的平均数是(92×6+94×12+96×15+98×18+100×9)÷60
=(552+1128+1440+1764+900)÷60
=5784÷60
=96.4.
故选:D.
(2014)22.七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用水量x/m3 0<x≤5 5<x≤10 10<x≤15 15<x≤20 x>20
频数/户 12 20 3
频率 0.12 0.07
若该小区有800户家庭,据此估计该小区月均用水量不超过10m3的家庭约有 户.
【分析】 根据=总数之间的关系求出5<x≤10的频数,再用整体×样本的百分比即可得出答案.
【解答】:根据题意得:=100(户),15<x≤20的频数是0.07×100=7(户),
5<x≤10的频数是:100﹣12﹣20﹣7﹣3=58(户),
则该小区月均用水量不超过10m3的家庭约有×800=560(户);故答案为:560.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
