15.1.2幂的乘方
图片预览





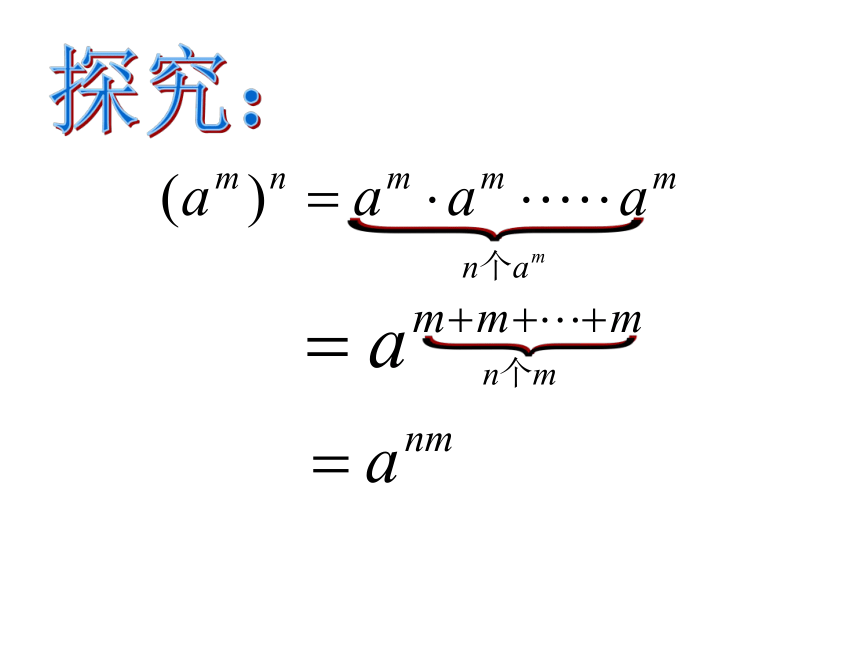


文档简介
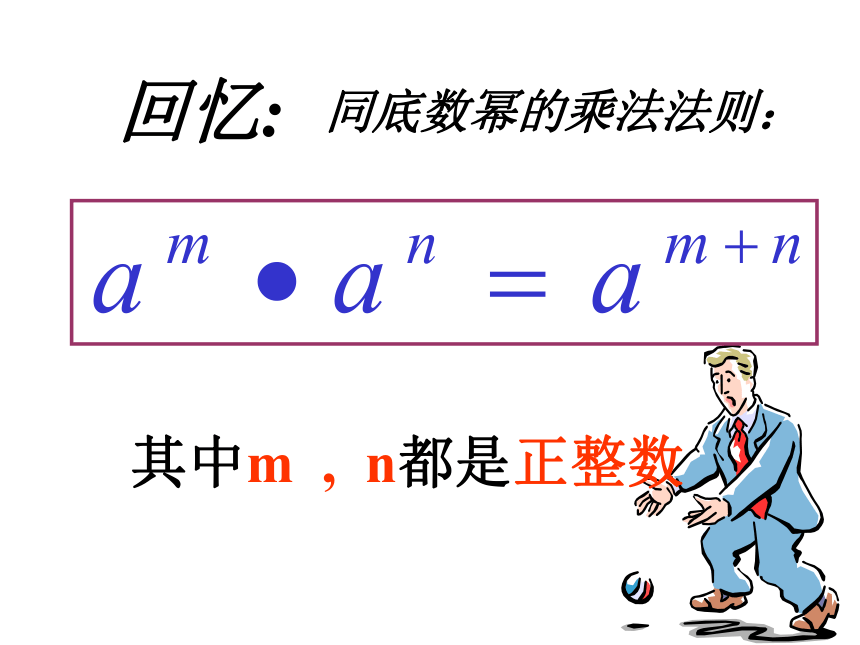
课件22张PPT。回忆: 其中m , n都是正整数同底数幂的乘法法则:练 习15.1.2 幂的乘方学习目标1、掌握幂的乘方法则和法则的推导过程;
2、运用幂的乘方法则熟练地进行计算。自学指导1、自学第142页内容,运用乘方的意义及同底数幂乘法法则怎样推出
?
幂的乘方法则什么?
2、自学第143页例2,看一看如何运用幂的乘方法则进行计算?自学时间5分钟探究: 根据乘方的意义及同底数的幂的乘法法则填空,并观察有什么规律?663m{{探究:幂的乘方法则:结论:符号叙述:语言叙述:幂的乘方,
底数不变,
指数相乘应用:想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?幂的乘方法则:(其中m , n都是正整数)同底数幂的乘法法则:底数不变指数相乘指数相加同底数幂相乘幂的乘方其中m , n都是正整数口答:⑴ (a2)4⑵(b3m)4⑶ (xn)m⑷ (b3)3⑸ x4·x4⑹ (x4)7
⑻ (a3)3⑽ (x6)5⑺ -(y7)2⑾ [(x+y)3]4⑼ [(-1)3]5 ⑿ [(a+1)3]n抢答:⑴ (an+1)2⑵ (am)3⑶ (410)5⑷ [(-1)3]4⑸ -4(a2)3⑹[(a+b)2]5⑺ (mn)n+1⑻ (x2a)3⑼ (y3)m+32,下列计算有错吗?有,请改正。3,计算:思考题:1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672动脑筋!小结:1,幂乘方法则:
语言叙述______________
符号叙述______________2,幂的乘方法则的逆用:3,多重乘方:综合拓展通过计算比较下列各组中两个数的大小:
A 12____21; B 23_____32; C 34_____43;
D 45_____54; E 56_____65;……;
(2) 由题(1)的结果归纳猜想出n n+1和(n+1)n的大小关系是_________;
(3) 根据上面的结论比较20042005和20052004大小关系是________.
作业日清试卷
2、运用幂的乘方法则熟练地进行计算。自学指导1、自学第142页内容,运用乘方的意义及同底数幂乘法法则怎样推出
?
幂的乘方法则什么?
2、自学第143页例2,看一看如何运用幂的乘方法则进行计算?自学时间5分钟探究: 根据乘方的意义及同底数的幂的乘法法则填空,并观察有什么规律?663m{{探究:幂的乘方法则:结论:符号叙述:语言叙述:幂的乘方,
底数不变,
指数相乘应用:想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?幂的乘方法则:(其中m , n都是正整数)同底数幂的乘法法则:底数不变指数相乘指数相加同底数幂相乘幂的乘方其中m , n都是正整数口答:⑴ (a2)4⑵(b3m)4⑶ (xn)m⑷ (b3)3⑸ x4·x4⑹ (x4)7
⑻ (a3)3⑽ (x6)5⑺ -(y7)2⑾ [(x+y)3]4⑼ [(-1)3]5 ⑿ [(a+1)3]n抢答:⑴ (an+1)2⑵ (am)3⑶ (410)5⑷ [(-1)3]4⑸ -4(a2)3⑹[(a+b)2]5⑺ (mn)n+1⑻ (x2a)3⑼ (y3)m+32,下列计算有错吗?有,请改正。3,计算:思考题:1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672动脑筋!小结:1,幂乘方法则:
语言叙述______________
符号叙述______________2,幂的乘方法则的逆用:3,多重乘方:综合拓展通过计算比较下列各组中两个数的大小:
A 12____21; B 23_____32; C 34_____43;
D 45_____54; E 56_____65;……;
(2) 由题(1)的结果归纳猜想出n n+1和(n+1)n的大小关系是_________;
(3) 根据上面的结论比较20042005和20052004大小关系是________.
作业日清试卷
