华东师大版七年级下册数学 9.3.2用多种正多边形铺设地面 课件 (共24张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 9.3.2用多种正多边形铺设地面 课件 (共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 906.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 08:08:20 | ||
图片预览




文档简介
(共24张PPT)
第9章 多边形
9.3.2 用多种正多边形铺设地面
华东师大·七年级下册
复习旧知 导入新课
1.在同种正多边形中,可以铺满地板的有哪些?
2.用同种正多边形瓷砖铺满地面,既不留空隙,又不重叠的关键是什么?
正三角形,正方形,正六边形
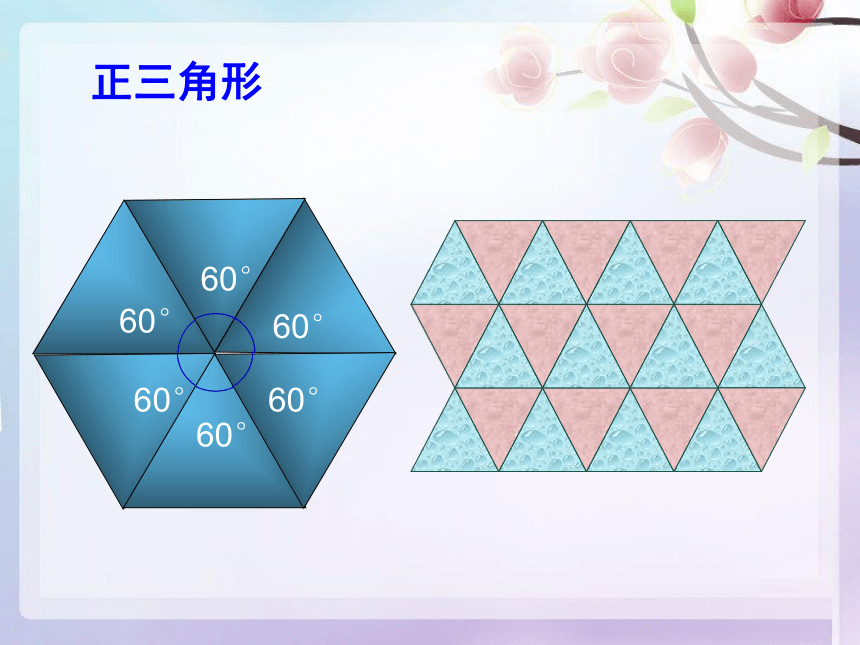
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面。
正三角形
60°
60°
60°
60°
60°
60°
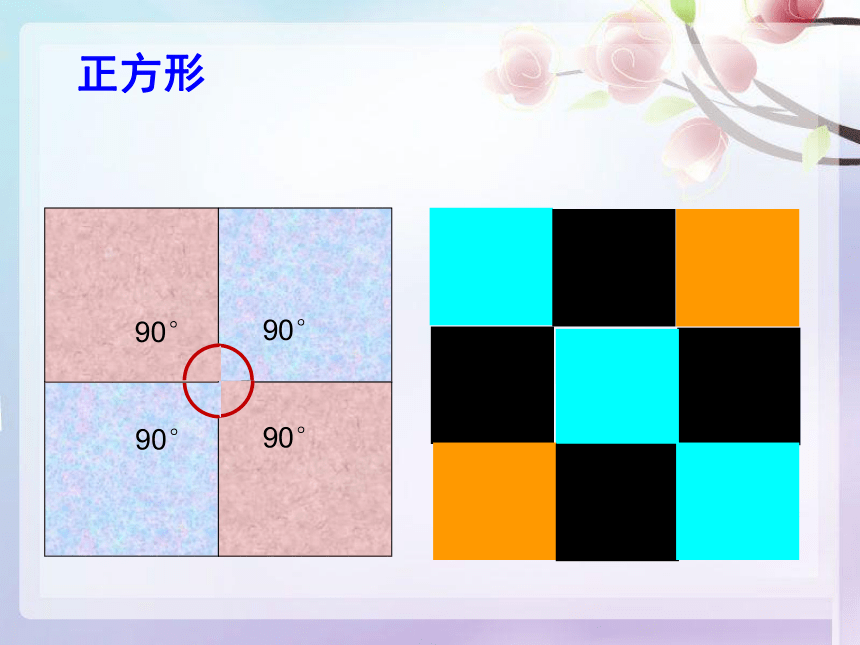
正方形
90°
90°
90°
90°
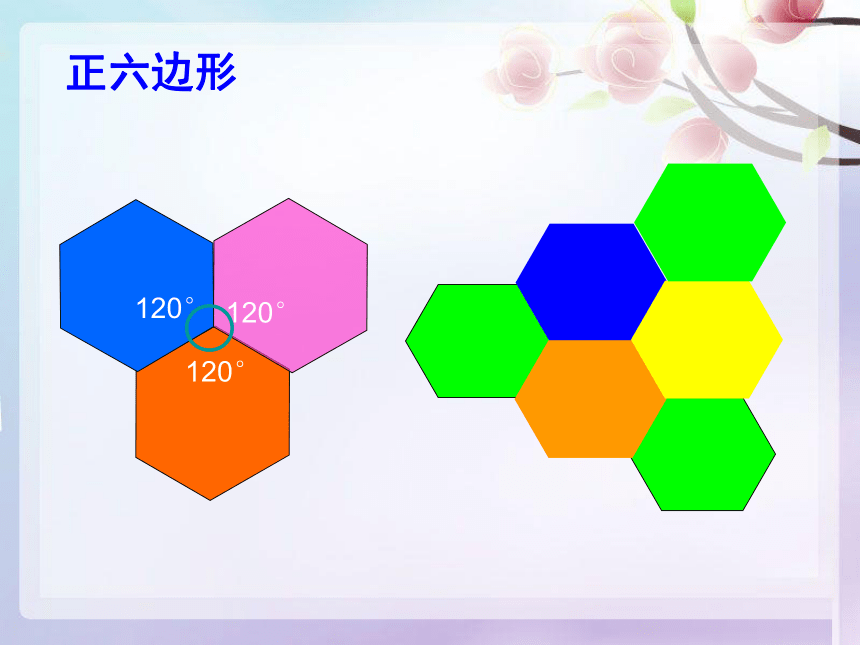
正六边形
120°
120°
120°
实践探究 理论验证
问 题:
用不同正多边形是否也能铺满地面呢?如果可以,那么你能找出几种不同的组合?你是如何找到的?
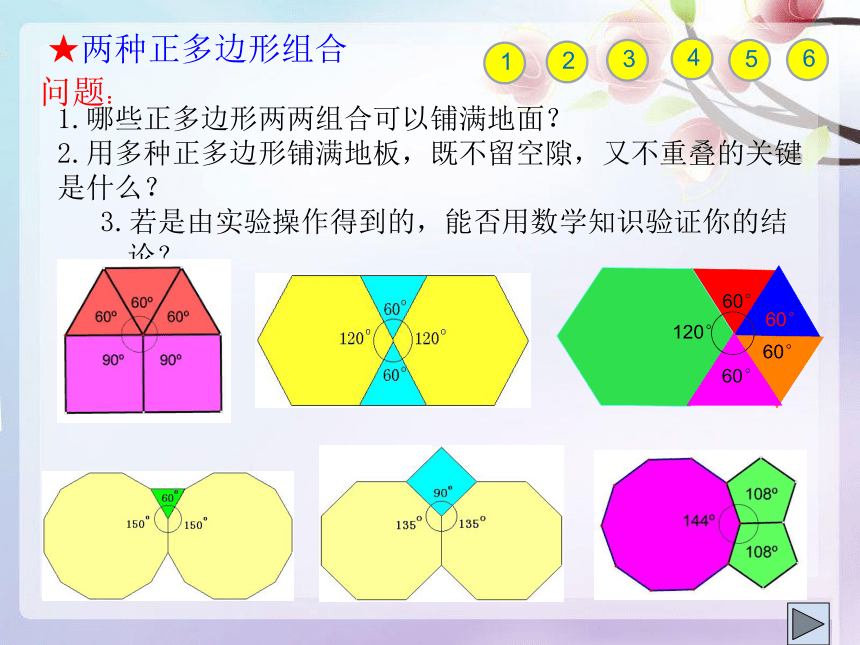
★两种正多边形组合
1.哪些正多边形两两组合可以铺满地面?
2.用多种正多边形铺满地板,既不留空隙,又不重叠的关键是什么?
3.若是由实验操作得到的,能否用数学知识验证你的结论?
120°
60°
60°
60°
60°
问题:
1
2
3
4
5
6
90
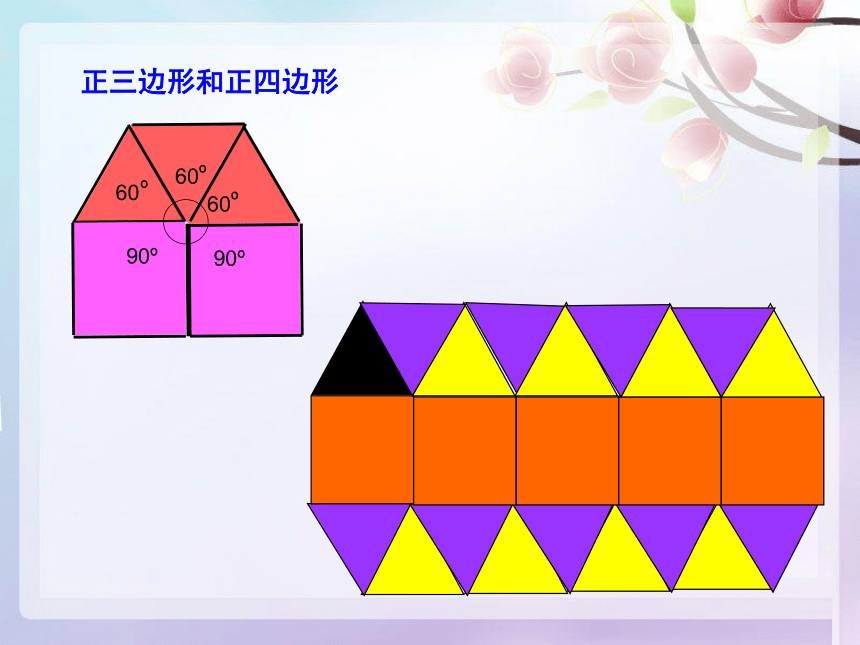
正三边形和正四边形
60
60
60
90
正三边形和正六边形
120°
60°
60°
60°
60°
正三边形和正十二边形
正四边形和正八边形
正五边形和正十边形?
围绕一点能拼成360 ,但能扩展到整个平面,即铺满地面吗?
尽管能围绕一点拼成360 ,但不能扩展到整个平面。
正五边形和正十边形?
★特殊情况:
一定要牢记
★两种正多边形组合
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面。
120°
60°
60°
60°
60°
1.哪些正多边形两两组合可以铺满地板?
2.用多种正多边形铺满地板,既不留空隙,又不重叠的关键是什么?
3.能否用数学知识验证你的结论?
正34、正36、正3-12、正48(共四种)
★三种正多边形组合
1.哪三种正多边形组合可以铺满地板?
2.用多种正多边形铺满地板,既不留空隙,又不重叠的关键是什么?
3.能否用数学知识验证你的结论?
问题:
1
2
3
正三边形、正四边形、正四边形
正三边形、正四边形和正十二边形
正四边形、正六边形和正十二边形
★三种正多边形组合
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面。
1.哪三种正多边形组合可以铺满地板?
2.用多种正多边形铺满地板,既不留空隙,又不重叠的关键是什么?
3.能否用数学理论验证你的结论?
问题:
正346、正34-12、正46-12(共三种)
★四种正多边形组合
60 +90 +108 +120 =378 >360
四种边数少的正多边形:正三角形、正方形、正五边形、正六边形,它们的内角和:
故四种以上正多边形不能拼地板
问题:四种正多边形能否铺满地面?
总结概括 巩固新知
★注意事项:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面。如:正五边形与正十边形的组合。
★ 当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面。
★多种正多边形能够铺满地面的组合:
二种组合(共4种):34,36,3-12,48
三种组合(共3种):346,34-12,46-12
随堂演练 提升水平
4.某中学阅览室在装修过程中,准备用边长相等的正方形和正三角形两种地砖铺满地面,在每个顶点的周围,正方形,正三角形地砖的块数可以分别是( )
A.2,2 B.2,3 C.1,2 D.2,1
1.用两种正多边形进行铺地,不能与正三角形匹配的多边形是( ).
A.正方形 B.正六边形 C.正十二边形 D.正十八边形
2.不能铺成平面图案的正多边形组合为( ).
A.正方形和正三角形 B.正方形和正八边形
C.正三角形和正十二边形 D.正方形和正六边形
3.某中学新科技馆铺设地面,已有正三角形状的地砖,现打算购买另一种不同形状的正多边形地砖,则该学校不应该购买的地砖形状是( )
A.正方形 B.正六边形 C.正八边形 D.正十二边形
D
D
C
B
5、如图①,②,③,用一种大小相等的正多边形密铺成一个“环”,我们称之为环形密铺.但图④,⑤不是我们所说的环形密铺.请你再写出一种可以进行环形密铺的正多边形:_____________
正十二边形
布置作业 检验真知
《同步练习册》P58-59
第9章 多边形
9.3.2 用多种正多边形铺设地面
华东师大·七年级下册
复习旧知 导入新课
1.在同种正多边形中,可以铺满地板的有哪些?
2.用同种正多边形瓷砖铺满地面,既不留空隙,又不重叠的关键是什么?
正三角形,正方形,正六边形
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面。
正三角形
60°
60°
60°
60°
60°
60°
正方形
90°
90°
90°
90°
正六边形
120°
120°
120°
实践探究 理论验证
问 题:
用不同正多边形是否也能铺满地面呢?如果可以,那么你能找出几种不同的组合?你是如何找到的?
★两种正多边形组合
1.哪些正多边形两两组合可以铺满地面?
2.用多种正多边形铺满地板,既不留空隙,又不重叠的关键是什么?
3.若是由实验操作得到的,能否用数学知识验证你的结论?
120°
60°
60°
60°
60°
问题:
1
2
3
4
5
6
90
正三边形和正四边形
60
60
60
90
正三边形和正六边形
120°
60°
60°
60°
60°
正三边形和正十二边形
正四边形和正八边形
正五边形和正十边形?
围绕一点能拼成360 ,但能扩展到整个平面,即铺满地面吗?
尽管能围绕一点拼成360 ,但不能扩展到整个平面。
正五边形和正十边形?
★特殊情况:
一定要牢记
★两种正多边形组合
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面。
120°
60°
60°
60°
60°
1.哪些正多边形两两组合可以铺满地板?
2.用多种正多边形铺满地板,既不留空隙,又不重叠的关键是什么?
3.能否用数学知识验证你的结论?
正34、正36、正3-12、正48(共四种)
★三种正多边形组合
1.哪三种正多边形组合可以铺满地板?
2.用多种正多边形铺满地板,既不留空隙,又不重叠的关键是什么?
3.能否用数学知识验证你的结论?
问题:
1
2
3
正三边形、正四边形、正四边形
正三边形、正四边形和正十二边形
正四边形、正六边形和正十二边形
★三种正多边形组合
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面。
1.哪三种正多边形组合可以铺满地板?
2.用多种正多边形铺满地板,既不留空隙,又不重叠的关键是什么?
3.能否用数学理论验证你的结论?
问题:
正346、正34-12、正46-12(共三种)
★四种正多边形组合
60 +90 +108 +120 =378 >360
四种边数少的正多边形:正三角形、正方形、正五边形、正六边形,它们的内角和:
故四种以上正多边形不能拼地板
问题:四种正多边形能否铺满地面?
总结概括 巩固新知
★注意事项:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面。如:正五边形与正十边形的组合。
★ 当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面。
★多种正多边形能够铺满地面的组合:
二种组合(共4种):34,36,3-12,48
三种组合(共3种):346,34-12,46-12
随堂演练 提升水平
4.某中学阅览室在装修过程中,准备用边长相等的正方形和正三角形两种地砖铺满地面,在每个顶点的周围,正方形,正三角形地砖的块数可以分别是( )
A.2,2 B.2,3 C.1,2 D.2,1
1.用两种正多边形进行铺地,不能与正三角形匹配的多边形是( ).
A.正方形 B.正六边形 C.正十二边形 D.正十八边形
2.不能铺成平面图案的正多边形组合为( ).
A.正方形和正三角形 B.正方形和正八边形
C.正三角形和正十二边形 D.正方形和正六边形
3.某中学新科技馆铺设地面,已有正三角形状的地砖,现打算购买另一种不同形状的正多边形地砖,则该学校不应该购买的地砖形状是( )
A.正方形 B.正六边形 C.正八边形 D.正十二边形
D
D
C
B
5、如图①,②,③,用一种大小相等的正多边形密铺成一个“环”,我们称之为环形密铺.但图④,⑤不是我们所说的环形密铺.请你再写出一种可以进行环形密铺的正多边形:_____________
正十二边形
布置作业 检验真知
《同步练习册》P58-59
