2022版高中数学第二章点直线平面之间的位置关系本章复习提升(word解析版)新人教A版必修2
文档属性
| 名称 | 2022版高中数学第二章点直线平面之间的位置关系本章复习提升(word解析版)新人教A版必修2 |  | |
| 格式 | zip | ||
| 文件大小 | 200.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-25 16:25:05 | ||
图片预览



文档简介
本章复习提升
易混易错练
易错点1 对空间角概念不清而致错
1.(2021宁夏六盘山高级中学高一上期末,)将正方形 ABCD沿对角线BD折成直二面角 A-BD-C,有如下四个结论:
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面 BCD成 60°的角;
④AB与 CD所成的角为 60°.
其中正确结论的个数是 ( )
A.1 B.2 C.3 D.4
2.(2020上海崇明高三一模,)已知AB⊥BC,BC⊥CD,DE⊥AE,DE∥BC,且AB=BC=CD,异面直线AB与CD成60°角,则异面直线AD与BC所成的角为 .
3.(2021广西北海高一上期末,)如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.
(1)求异面直线AP与BC所成角的余弦值;
(2)求证:PD⊥平面PBC;
(3)求直线AB与平面PBC所成角的正弦值.
易错点2 对有关平行、垂直的概念和定理理解不透彻
4.(2021宁夏银川兴庆高一上期末,)已知m,n是两条不重合的直线,α,β是不重合的平面,则下面四个结论中正确的是 ( )
A.若m α,n β,m⊥n,则α⊥β
B.若m∥α,m⊥n,则n⊥α
C.若m⊥n,m⊥β,则n∥β
D.若m⊥α,m∥n,n⊥β,则α∥β
5.(2021内蒙古包头高三上期末,)已知直线b,平面α,有以下条件:
①b与α内一条直线平行;
②b与α内所有直线都没有公共点;
③b与α无公共点;
④b不在α内,且与α内的一条直线平行.
其中能推出b∥α的条件有 .(把你认为正确的序号都填上)
易错点3 考虑问题不全面而致错
6.(2020四川师大附中高二上月考,)如果一条直线与一个平面平行,夹在直线和平面间的两线段相等,那么这两条线段所在直线的位置关系是 .
7.(2020江苏徐州高一下期末,)已知平面α∥平面β,P是α,β外一点,过P点的两条直线AC,BD分别交α于点A,B,交β于点C,D,且PA=6,AC=9,AB=8,求CD的长.
思想方法练
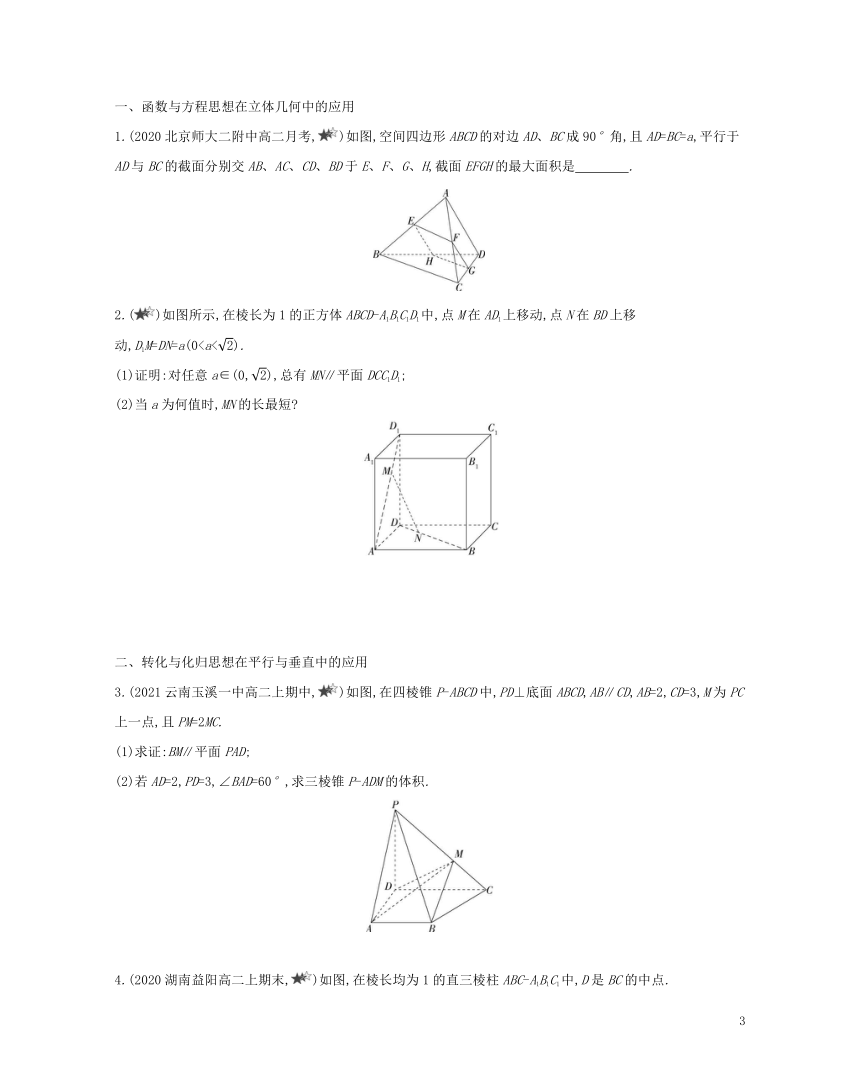
一、函数与方程思想在立体几何中的应用
1.(2020北京师大二附中高二月考,)如图,空间四边形ABCD的对边AD、BC成90°角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H,截面EFGH的最大面积是 .
2.()如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点M在AD1上移动,点N在BD上移动,D1M=DN=a(0(1)证明:对任意a∈(0,),总有MN∥平面DCC1D1;
(2)当a为何值时,MN的长最短
二、转化与化归思想在平行与垂直中的应用
3.(2021云南玉溪一中高二上期中,)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若AD=2,PD=3,∠BAD=60°,求三棱锥P-ADM的体积.
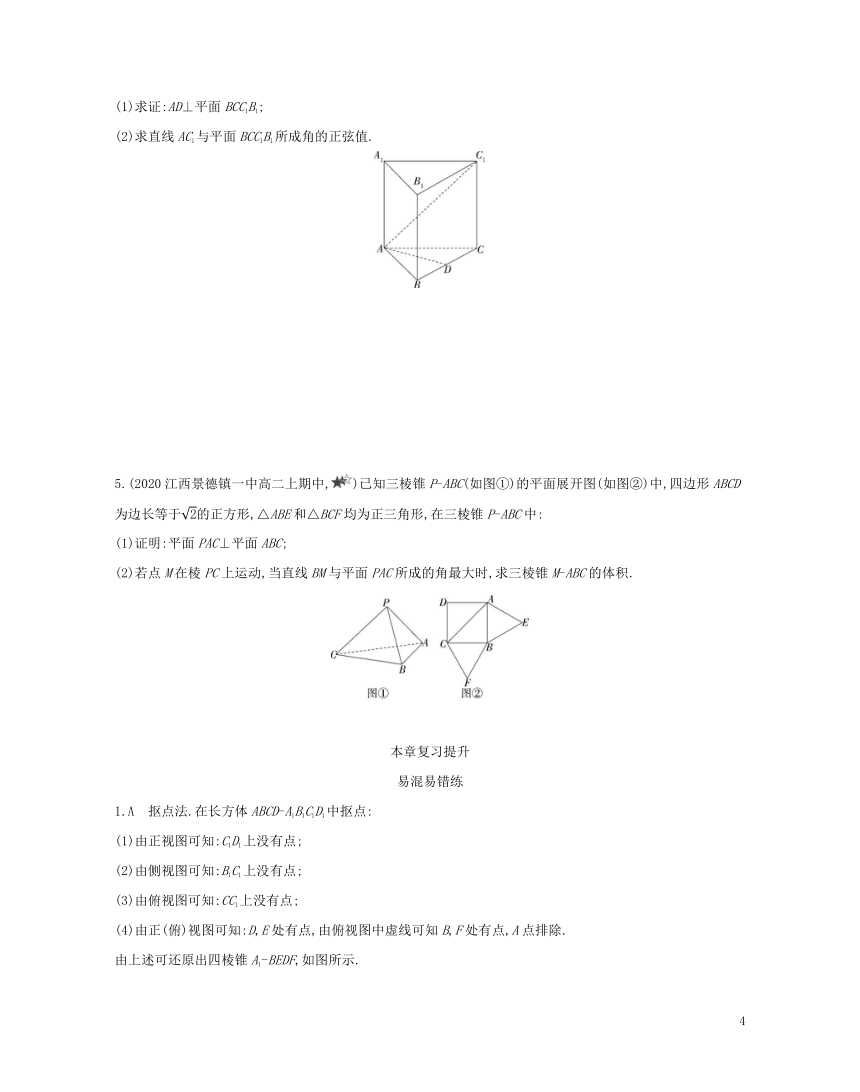
4.(2020湖南益阳高二上期末,)如图,在棱长均为1的直三棱柱ABC-A1B1C1中,D是BC的中点.
(1)求证:AD⊥平面BCC1B1;
(2)求直线AC1与平面BCC1B1所成角的正弦值.
5.(2020江西景德镇一中高二上期中,)已知三棱锥P-ABC(如图①)的平面展开图(如图②)中,四边形ABCD为边长等于的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
(1)证明:平面PAC⊥平面ABC;
(2)若点M在棱PC上运动,当直线BM与平面PAC所成的角最大时,求三棱锥M-ABC的体积.
本章复习提升
易混易错练
1.A 抠点法.在长方体ABCD-A1B1C1D1中抠点:
(1)由正视图可知:C1D1上没有点;
(2)由侧视图可知:B1C1上没有点;
(3)由俯视图可知:CC1上没有点;
(4)由正(俯)视图可知:D,E处有点,由俯视图中虚线可知B,F处有点,A点排除.
由上述可还原出四棱锥A1-BEDF,如图所示.
S四边形BEDF=1×1=1,=×1×1=.故选A.
易错警示
1.由三视图还原直观图时,要注意实线与虚线的区别.
2.要清楚几何体的结构特征,否则会导致漏算或者多算几何体的表面积或者体积.
2.D A的正视图和俯视图不符合要求,B的正视图和侧视图不符合要求,C的侧视图和俯视图不符合要求.
3.答案 61π
解析 解法一:由已知得球的半径为5,而圆台的下底面半径为5,∴下底面为球的大圆面,将圆台补为圆锥,如图,则O2B=O2C=5,O1C=4,
∴O1O2==3,
设EO1=x,则=,∴x=12,
即O1E=12,∴O2E=15,
∴V圆台=×π×52×15-×π×42×12=125π-64π=61π.
解法二:依题意可知圆台的下底面为球的大圆面,
则圆台的高h==3,
故圆台的体积V=×π×3×(52+42+5×4)=61π.
易错警示
要熟记几何体的表面积、体积公式,尤其是不常考的台体的表面积及体积公式.
4.解析 由题意知,旋转后得到的几何体是一个挖去一个圆柱的圆锥,且圆锥的底面半径为4,高为4,圆柱的底面半径为2,高为2,
圆锥的底面积为16π,圆锥的侧面积为π×4×8=32π,圆柱的侧面积为2π×2×2=8π,
∴所求几何体的表面积为16π+32π+8π=48π+8π.
易错警示
挖去圆柱后的几何体的表面积多了一个圆柱的侧面积,但圆锥的底面积并没有减少,因为圆柱的上底面面积对圆锥底面缺失的部分面积进行了等量补充,解题时要注意正确分析几何体的结构,避免计算错误.
5.答案 (1+)π或π
解析 若绕一条直角边所在直线旋转一周,则形成的几何体为圆锥,该圆锥的底面半径为1,高为1,所以母线长为,其表面积为π××1+π×12=(1+)π;
若绕斜边所在直线旋转一周,则得到的是两个同底的圆锥组合在一起的几何体,圆锥底面半径为,母线长为1,该几何体的表面积为2×π×1×=π.
综上所述,该几何体的表面积为(1+)π或π.
易错警示
遇到带有分类讨论性质的题目时,要跳出定性思维的限制,将问题分析全面,防止漏解.
6.答案 或
解析 当母线长为a时,圆柱的底面半径是,此时圆柱的体积是π××a=;
当母线长为2a时,圆柱的底面半径是,此时圆柱的体积是π××2a=.
综上,圆柱的体积是或.
易错警示 圆柱的侧面展开图是矩形,其每一条边都有可能是母线,不能简单地认为长的一边或短的一边是母线.
7.解析 设球的半径为r,则球的体积为πr3,球心到该圆锥底面的距离为,于是圆锥的底面半径为=,高为或.若高为,如图所示,则该圆锥的体积为×π××=πr3,∴该圆锥的体积和此球体积的比值为=.同理可得高为时,比值为.
8.解析 当两截面圆在球心O的同侧时,如图(1)所示,AB为较大的截面圆的直径,O1为较大的截面圆的圆心,CD为较小的截面圆的直径,O2为较小的截面圆的圆心,梯形ABDC为圆台的轴截面,由题意,知OO1=3,OO2=4,则圆台的高O1O2=1,AC=,所以S圆台侧=π(3+4)×=7π.
图(1)
当两截面圆在球心O的异侧时,如图(2)所示,AB为较大的截面圆的直径,O1为较大的截面圆的圆心,CD为较小的截面圆的直径,O2为较小的截面圆的圆心,梯形ABDC为圆台的轴截面,由题意,知OO1=3,OO2=4,则圆台的高O1O2=7,AC=5,所以S圆台侧=π(3+4)×5=35π.
图(2)
思想方法练
1.答案 43π
解析 三棱锥A-BCD中,AB=CD=6,AC=BD=AD=BC=5,
将此三棱锥放入一个面对角线长分别为5,5,6的长方体中,
设长方体共顶点的三条棱长分别为x,y,z,
则可得x2+y2+z2=43,
设三棱锥的外接球的半径为R,则4R2=x2+y2+z2=43,所以R=,
经分析知长方体的外接球为该三棱锥的外接球,则长方体的体对角线的长度为该三棱锥的外接球的直径,利用方程的思想,构建外接球直径与长方体体对角线的等量关系,使问题顺利得到解决.
故该三棱锥的外接球的表面积S=4π×=43π.故答案为43π.
思想方法
方程思想是指从分析问题的数量关系入手,将问题中的已知量和未知量之间的数量关系通过适当设元建立方程(组),然后通过解方程(组)使问题得到解决的思维方式.用方程思想解题的关键是利用已知条件或公式、定理构造方程(组).立体几何中常见的考题是利用题设中的等式求几何体的某一变量,进而求几何体的表面积、体积,或者利用几何体中的等量关系结合直角三角形并利用勾股定理求解球的半径等.
2.解析 (1)圆锥的母线长为=2(cm),
所以圆锥的侧面积S1=π×2×2=4π(cm2).
(2)圆锥的轴截面如图所示.
设圆柱的底面半径为rcm,高为xcm,
则=,∴r=,
∴圆柱的侧面积S2=2πrx=(-x2+6x)=-[(x-3)2-9],
构建关于x的二次函数,通过二次函数的最值解决问题.
∴当x=3时,圆柱的侧面积最大,最大侧面积为6πcm2.
思想方法
函数思想,是指用函数的概念和性质去分析问题、转化问题和解决问题.函数思想在立体几何中常见的考题是点的轨迹问题、距离的最值问题、几何体表面积或体积的最值问题.做题时,一定要注意根据题意,构建好有关几何量的函数关系式,然后利用函数的有关性质,结合函数的图象解决问题.
3.解析 由题意易知,三棱锥P-DCE为正三棱锥,各侧棱长均为1,P点在底面DCE的投影为等边△DCE的中心,设中心为O,则OD=OE=OC=,在Rt△POD中,OP2=PD2-OD2=,则OP=.易知外接球的球心必在OP上,设球心为O',则O'P=O'D,设O'P=O'D=R,
则在Rt△OO'D中,OO'2+OD2=O'D2,即(OP-O'P)2+OD2=O'D2,∴+=R2,解得R=,∴三棱锥P-DCE的外接球的体积为πR3=.
解决几何体的外接球问题,关键是找准球心的位置,将球心放在能够求解的三角形中,利用三角形已知的边角关系构建方程,从而解决问题.
4.C 设三棱台的高为h,S△ABC=S,则=4S.
∴=S△ABC·h=,
=·h=,
又V三棱台=h(S+4S+)=,
∴=V三棱台--
=--=.
直接计算三棱锥B-A1B1C的体积难度较大,可以采用“正难则反”的转化与化归思想使问题得到解决.
∴所求体积之比为1∶2∶4.
思想方法
转化与化归思想就是在研究和解决有关数学问题时采用某种手段将问题通过变换 使之转化,进而得到解决的一种方法.其核心就是把未知转化为已知,将未能解决的问题划归为已经解决的问题.在立体几何中常见的转化形式有正难则反,特殊与一般的转换,空间与平面的转换,等积转换等.
5.B 因为正四面体可以在圆锥内任意转动,所以该正四面体的棱长最大时内接于圆锥的内切球,
直接研究正四面体内接于圆锥时,等式关系不容易建立,问题不便于解决,利用转化与化归思想将问题转化为正四面体内接于球,球内切于圆锥,就可以实现复杂问题简单化.
圆锥的轴截面如图(1)所示,设球心为P,球的半径为r,轴截面上球与圆锥母线的切点为Q,
则OA=OB=,OS=,则tan∠SAO=,即∠SAO=60°,则△SAB为等边三角形,
故P是△SAB的中心,连接BP,则BP平分∠SBA,所以∠PBO=30°,
所以tan30°=,即r=OB=,即正四面体的外接球的半径为r=,
图(1)
另正四面体可以从正方体中截得,如图(2),
图(2)
从图中可得,当正四面体的棱长为a时,截得它的正方体的棱长为a,
而正四面体的四个顶点为正方体的顶点,故正四面体的外接球即为截得它的正方体的外接球,所以2r=×a=a,∴r=a,
求解正四面体的外接球半径时,利用转化与化归思想将问题转化为求解正方体的体对角线,使问题得到了进一步的简化.
又r=,所以a=.
故选B.
6.解析 如图所示,在三棱锥A1-ABD中,AA1是三棱锥A1-ABD的高,AB=AD=AA1=a,A1B=BD=A1D=a.
∵=,=×a××a=a2,
运用等体积法将其转化.
∴×a2×a=×a2×d,∴d=a.
故A到平面A1BD的距离为a.
10
易混易错练
易错点1 对空间角概念不清而致错
1.(2021宁夏六盘山高级中学高一上期末,)将正方形 ABCD沿对角线BD折成直二面角 A-BD-C,有如下四个结论:
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面 BCD成 60°的角;
④AB与 CD所成的角为 60°.
其中正确结论的个数是 ( )
A.1 B.2 C.3 D.4
2.(2020上海崇明高三一模,)已知AB⊥BC,BC⊥CD,DE⊥AE,DE∥BC,且AB=BC=CD,异面直线AB与CD成60°角,则异面直线AD与BC所成的角为 .
3.(2021广西北海高一上期末,)如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.
(1)求异面直线AP与BC所成角的余弦值;
(2)求证:PD⊥平面PBC;
(3)求直线AB与平面PBC所成角的正弦值.
易错点2 对有关平行、垂直的概念和定理理解不透彻
4.(2021宁夏银川兴庆高一上期末,)已知m,n是两条不重合的直线,α,β是不重合的平面,则下面四个结论中正确的是 ( )
A.若m α,n β,m⊥n,则α⊥β
B.若m∥α,m⊥n,则n⊥α
C.若m⊥n,m⊥β,则n∥β
D.若m⊥α,m∥n,n⊥β,则α∥β
5.(2021内蒙古包头高三上期末,)已知直线b,平面α,有以下条件:
①b与α内一条直线平行;
②b与α内所有直线都没有公共点;
③b与α无公共点;
④b不在α内,且与α内的一条直线平行.
其中能推出b∥α的条件有 .(把你认为正确的序号都填上)
易错点3 考虑问题不全面而致错
6.(2020四川师大附中高二上月考,)如果一条直线与一个平面平行,夹在直线和平面间的两线段相等,那么这两条线段所在直线的位置关系是 .
7.(2020江苏徐州高一下期末,)已知平面α∥平面β,P是α,β外一点,过P点的两条直线AC,BD分别交α于点A,B,交β于点C,D,且PA=6,AC=9,AB=8,求CD的长.
思想方法练
一、函数与方程思想在立体几何中的应用
1.(2020北京师大二附中高二月考,)如图,空间四边形ABCD的对边AD、BC成90°角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H,截面EFGH的最大面积是 .
2.()如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点M在AD1上移动,点N在BD上移动,D1M=DN=a(0
(2)当a为何值时,MN的长最短
二、转化与化归思想在平行与垂直中的应用
3.(2021云南玉溪一中高二上期中,)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若AD=2,PD=3,∠BAD=60°,求三棱锥P-ADM的体积.
4.(2020湖南益阳高二上期末,)如图,在棱长均为1的直三棱柱ABC-A1B1C1中,D是BC的中点.
(1)求证:AD⊥平面BCC1B1;
(2)求直线AC1与平面BCC1B1所成角的正弦值.
5.(2020江西景德镇一中高二上期中,)已知三棱锥P-ABC(如图①)的平面展开图(如图②)中,四边形ABCD为边长等于的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
(1)证明:平面PAC⊥平面ABC;
(2)若点M在棱PC上运动,当直线BM与平面PAC所成的角最大时,求三棱锥M-ABC的体积.
本章复习提升
易混易错练
1.A 抠点法.在长方体ABCD-A1B1C1D1中抠点:
(1)由正视图可知:C1D1上没有点;
(2)由侧视图可知:B1C1上没有点;
(3)由俯视图可知:CC1上没有点;
(4)由正(俯)视图可知:D,E处有点,由俯视图中虚线可知B,F处有点,A点排除.
由上述可还原出四棱锥A1-BEDF,如图所示.
S四边形BEDF=1×1=1,=×1×1=.故选A.
易错警示
1.由三视图还原直观图时,要注意实线与虚线的区别.
2.要清楚几何体的结构特征,否则会导致漏算或者多算几何体的表面积或者体积.
2.D A的正视图和俯视图不符合要求,B的正视图和侧视图不符合要求,C的侧视图和俯视图不符合要求.
3.答案 61π
解析 解法一:由已知得球的半径为5,而圆台的下底面半径为5,∴下底面为球的大圆面,将圆台补为圆锥,如图,则O2B=O2C=5,O1C=4,
∴O1O2==3,
设EO1=x,则=,∴x=12,
即O1E=12,∴O2E=15,
∴V圆台=×π×52×15-×π×42×12=125π-64π=61π.
解法二:依题意可知圆台的下底面为球的大圆面,
则圆台的高h==3,
故圆台的体积V=×π×3×(52+42+5×4)=61π.
易错警示
要熟记几何体的表面积、体积公式,尤其是不常考的台体的表面积及体积公式.
4.解析 由题意知,旋转后得到的几何体是一个挖去一个圆柱的圆锥,且圆锥的底面半径为4,高为4,圆柱的底面半径为2,高为2,
圆锥的底面积为16π,圆锥的侧面积为π×4×8=32π,圆柱的侧面积为2π×2×2=8π,
∴所求几何体的表面积为16π+32π+8π=48π+8π.
易错警示
挖去圆柱后的几何体的表面积多了一个圆柱的侧面积,但圆锥的底面积并没有减少,因为圆柱的上底面面积对圆锥底面缺失的部分面积进行了等量补充,解题时要注意正确分析几何体的结构,避免计算错误.
5.答案 (1+)π或π
解析 若绕一条直角边所在直线旋转一周,则形成的几何体为圆锥,该圆锥的底面半径为1,高为1,所以母线长为,其表面积为π××1+π×12=(1+)π;
若绕斜边所在直线旋转一周,则得到的是两个同底的圆锥组合在一起的几何体,圆锥底面半径为,母线长为1,该几何体的表面积为2×π×1×=π.
综上所述,该几何体的表面积为(1+)π或π.
易错警示
遇到带有分类讨论性质的题目时,要跳出定性思维的限制,将问题分析全面,防止漏解.
6.答案 或
解析 当母线长为a时,圆柱的底面半径是,此时圆柱的体积是π××a=;
当母线长为2a时,圆柱的底面半径是,此时圆柱的体积是π××2a=.
综上,圆柱的体积是或.
易错警示 圆柱的侧面展开图是矩形,其每一条边都有可能是母线,不能简单地认为长的一边或短的一边是母线.
7.解析 设球的半径为r,则球的体积为πr3,球心到该圆锥底面的距离为,于是圆锥的底面半径为=,高为或.若高为,如图所示,则该圆锥的体积为×π××=πr3,∴该圆锥的体积和此球体积的比值为=.同理可得高为时,比值为.
8.解析 当两截面圆在球心O的同侧时,如图(1)所示,AB为较大的截面圆的直径,O1为较大的截面圆的圆心,CD为较小的截面圆的直径,O2为较小的截面圆的圆心,梯形ABDC为圆台的轴截面,由题意,知OO1=3,OO2=4,则圆台的高O1O2=1,AC=,所以S圆台侧=π(3+4)×=7π.
图(1)
当两截面圆在球心O的异侧时,如图(2)所示,AB为较大的截面圆的直径,O1为较大的截面圆的圆心,CD为较小的截面圆的直径,O2为较小的截面圆的圆心,梯形ABDC为圆台的轴截面,由题意,知OO1=3,OO2=4,则圆台的高O1O2=7,AC=5,所以S圆台侧=π(3+4)×5=35π.
图(2)
思想方法练
1.答案 43π
解析 三棱锥A-BCD中,AB=CD=6,AC=BD=AD=BC=5,
将此三棱锥放入一个面对角线长分别为5,5,6的长方体中,
设长方体共顶点的三条棱长分别为x,y,z,
则可得x2+y2+z2=43,
设三棱锥的外接球的半径为R,则4R2=x2+y2+z2=43,所以R=,
经分析知长方体的外接球为该三棱锥的外接球,则长方体的体对角线的长度为该三棱锥的外接球的直径,利用方程的思想,构建外接球直径与长方体体对角线的等量关系,使问题顺利得到解决.
故该三棱锥的外接球的表面积S=4π×=43π.故答案为43π.
思想方法
方程思想是指从分析问题的数量关系入手,将问题中的已知量和未知量之间的数量关系通过适当设元建立方程(组),然后通过解方程(组)使问题得到解决的思维方式.用方程思想解题的关键是利用已知条件或公式、定理构造方程(组).立体几何中常见的考题是利用题设中的等式求几何体的某一变量,进而求几何体的表面积、体积,或者利用几何体中的等量关系结合直角三角形并利用勾股定理求解球的半径等.
2.解析 (1)圆锥的母线长为=2(cm),
所以圆锥的侧面积S1=π×2×2=4π(cm2).
(2)圆锥的轴截面如图所示.
设圆柱的底面半径为rcm,高为xcm,
则=,∴r=,
∴圆柱的侧面积S2=2πrx=(-x2+6x)=-[(x-3)2-9],
构建关于x的二次函数,通过二次函数的最值解决问题.
∴当x=3时,圆柱的侧面积最大,最大侧面积为6πcm2.
思想方法
函数思想,是指用函数的概念和性质去分析问题、转化问题和解决问题.函数思想在立体几何中常见的考题是点的轨迹问题、距离的最值问题、几何体表面积或体积的最值问题.做题时,一定要注意根据题意,构建好有关几何量的函数关系式,然后利用函数的有关性质,结合函数的图象解决问题.
3.解析 由题意易知,三棱锥P-DCE为正三棱锥,各侧棱长均为1,P点在底面DCE的投影为等边△DCE的中心,设中心为O,则OD=OE=OC=,在Rt△POD中,OP2=PD2-OD2=,则OP=.易知外接球的球心必在OP上,设球心为O',则O'P=O'D,设O'P=O'D=R,
则在Rt△OO'D中,OO'2+OD2=O'D2,即(OP-O'P)2+OD2=O'D2,∴+=R2,解得R=,∴三棱锥P-DCE的外接球的体积为πR3=.
解决几何体的外接球问题,关键是找准球心的位置,将球心放在能够求解的三角形中,利用三角形已知的边角关系构建方程,从而解决问题.
4.C 设三棱台的高为h,S△ABC=S,则=4S.
∴=S△ABC·h=,
=·h=,
又V三棱台=h(S+4S+)=,
∴=V三棱台--
=--=.
直接计算三棱锥B-A1B1C的体积难度较大,可以采用“正难则反”的转化与化归思想使问题得到解决.
∴所求体积之比为1∶2∶4.
思想方法
转化与化归思想就是在研究和解决有关数学问题时采用某种手段将问题通过变换 使之转化,进而得到解决的一种方法.其核心就是把未知转化为已知,将未能解决的问题划归为已经解决的问题.在立体几何中常见的转化形式有正难则反,特殊与一般的转换,空间与平面的转换,等积转换等.
5.B 因为正四面体可以在圆锥内任意转动,所以该正四面体的棱长最大时内接于圆锥的内切球,
直接研究正四面体内接于圆锥时,等式关系不容易建立,问题不便于解决,利用转化与化归思想将问题转化为正四面体内接于球,球内切于圆锥,就可以实现复杂问题简单化.
圆锥的轴截面如图(1)所示,设球心为P,球的半径为r,轴截面上球与圆锥母线的切点为Q,
则OA=OB=,OS=,则tan∠SAO=,即∠SAO=60°,则△SAB为等边三角形,
故P是△SAB的中心,连接BP,则BP平分∠SBA,所以∠PBO=30°,
所以tan30°=,即r=OB=,即正四面体的外接球的半径为r=,
图(1)
另正四面体可以从正方体中截得,如图(2),
图(2)
从图中可得,当正四面体的棱长为a时,截得它的正方体的棱长为a,
而正四面体的四个顶点为正方体的顶点,故正四面体的外接球即为截得它的正方体的外接球,所以2r=×a=a,∴r=a,
求解正四面体的外接球半径时,利用转化与化归思想将问题转化为求解正方体的体对角线,使问题得到了进一步的简化.
又r=,所以a=.
故选B.
6.解析 如图所示,在三棱锥A1-ABD中,AA1是三棱锥A1-ABD的高,AB=AD=AA1=a,A1B=BD=A1D=a.
∵=,=×a××a=a2,
运用等体积法将其转化.
∴×a2×a=×a2×d,∴d=a.
故A到平面A1BD的距离为a.
10
