2021-2022学年北师大版数学八年级下册2.6一元一次不等式组课件(30张)
文档属性
| 名称 | 2021-2022学年北师大版数学八年级下册2.6一元一次不等式组课件(30张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 18:21:01 | ||
图片预览









文档简介
(共30张PPT)
2.6.1 一元一次不等式组
学习目标
1. 理解一元一次不等式组及其解的意义,加强运算的熟练性和准确性,培养思维的全面性.
2. 初步感知利用一元一次不等式解集的数轴表示求不等式组的解和解集的方法.
知识回顾
左右两边都是整式,只含一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
1. 一元一次不等式的定义
(1)去分母 (注意符号)
(2)去括号
(3)移项
(4)合并同类项
(5)未知数的系数化为1(注意符号)
2. 解一元一次不等式的一般步骤
新课导入
一个长方形足球场的宽为70m,如果它的周长大于350 m,面积小于7560 m2,求这个足球场的长x的取值范围,并判断这个足球场是否可以进行国际足球比赛(注:用于国际比赛的足球场的长在100至110 m之间,宽在64至75 m之间).
解:根据周长大于350 m,得
2(x+70)>350
根据面积小于7560 m2,得
70x<7560
①
②
x需同时满足①和②,你能求出它吗?.
带着这个问题开始今天的学习吧!
某校今年冬季烧煤取暖时间为4个月.如果每月比计划多烧5 t煤,那么取暖用煤总量将超过100 t;如果每月比计划少烧5 t煤,那么取暖用煤总量将不足68 t.
若该校计划每月烧煤x t,则x满足怎样的关系式?
解:根据题意,得
4(x+5)>100, ①
4(x-5)<68. ②
未知数x同时满足①②两个不等式,把①②两个不等式组合在一起,就组成了一个一元一次不等式组,记作
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
4(x+5)>100,
4(x-5)<68.
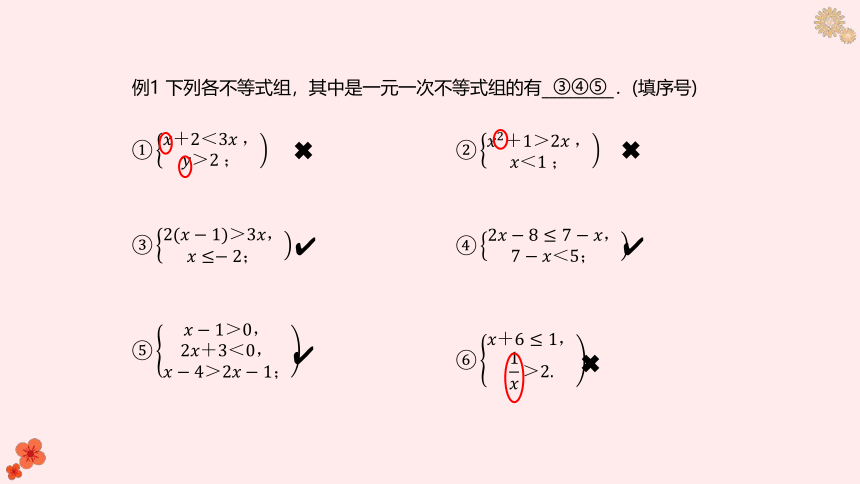
例1 下列各不等式组,其中是一元一次不等式组的有_________.(填序号)
③④⑤
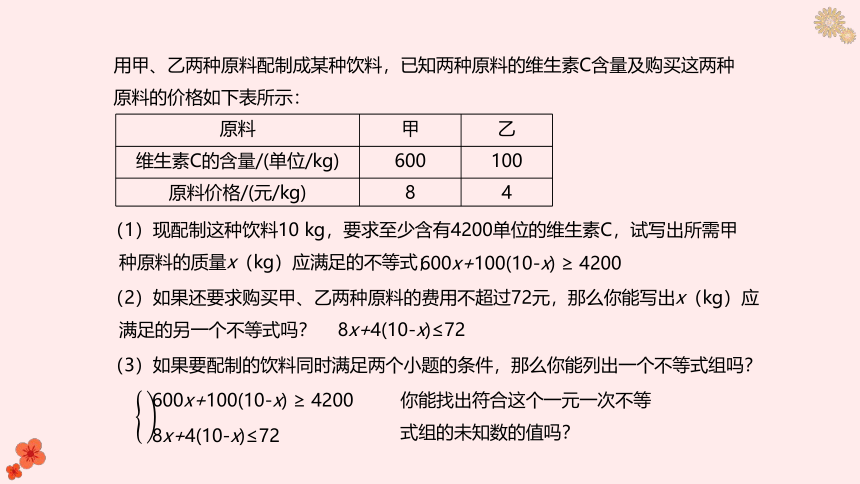
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
(1)现配制这种饮料10 kg,要求至少含有4200单位的维生素C,试写出所需甲种原料的质量x(kg)应满足的不等式;
600x+100(10-x) ≥ 4200
8x+4(10-x)≤72
(2)如果还要求购买甲、乙两种原料的费用不超过72元,那么你能写出x(kg)应满足的另一个不等式吗?
(3)如果要配制的饮料同时满足两个小题的条件,那么你能列出一个不等式组吗?
你能找出符合这个一元一次不等式组的未知数的值吗?
600x+100(10-x) ≥ 4200
8x+4(10-x)≤72
600x+100(10-x) ≥ 4200
8x+4(10-x)≤72
①
②
解:解不等式①,得
解不等式组:
x≥6.4 .
解不等式②,得
x≤8 .
在同一数轴上表示不等式①②的解集,如下图.
所以原不等式组的解集为:6.4≤x≤8.
公共部分
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集. 求不等式组解集的过程,叫做解不等式组.
例2 解不等式组: .
①
②
解:解不等式①,得 x>2 .
解不等式②,得 x>4 .
在同一个数轴上表示不等式①和②的解集:
∴原不等式组的解集为 x>4 .
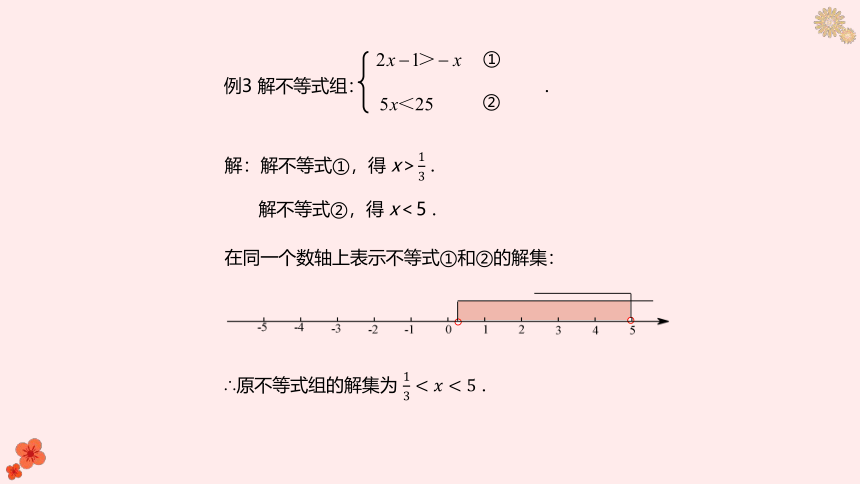
例3 解不等式组: .
①
②
解:解不等式①,得 x> .
解不等式②,得 x<5 .
在同一个数轴上表示不等式①和②的解集:
∴原不等式组的解集为 .
随堂练习
1. 下列不等式组中,是一元一次不等式组的是( )
A. B. C. D.
A
2. 已知点A(x+3,2x-4)在第四象限,则x的取值范围是__________.
-3<x<2
3. 不等式组的最小整数解是______.
0
解:(1)解不等式①,得x<1 .
解不等式②,得x<3 .
在数轴上表示不等式①和②的解集:
∴原不等式组的解集为x<1 .
(2)解不等式①,得x>-2.
解不等式②,得x>1.
∴原不等式组的解集为x>1.
4. 解下列不等式组,并把它们的解集在数轴上表示出来:
(1)
(2)
①
②
①
②
在数轴上表示不等式①和②的解集:
5. 解不等式组:
①
②
解:解不等式①,得x<-1 .
解不等式②,得x≥2 .
∴原不等式组无解.
在数轴上表示不等式①和②的解集:
课堂小结
不等式解集的四种情况(a>b)
① 的解集为x>a .
② 的解集为x<b .
③ 的解集为b<x<a.
④ 无解.
大大取大
小小取小
大小小大取中间
大大小小没得找
谢谢聆听
2.6.2 一元一次不等式组
学习目标
1. 会熟练地解复杂的一元一次不等式组.
2. 会根据题意列一元一次不等式组,解决实际问题.
知识回顾
1. 一元一次不等式组
(1)解每一个一元一次不等式;
(2)解集的表示:口诀法或数轴法.
2. 解一元一次不等式组的一般步骤
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
新课导入
在什么条件下,长度为3 cm,7 cm,x cm的三条线段可以围成一个三角形
你和同伴所列的不等式组一样吗 解集呢 与同伴交流.
3+7>x
7-3<x
解:根据三角形任意两边之和大于第三边,三角形任意两边之差小于第三边,得
解不等式①,得 x<10 .
解不等式②,得 x>4 .
在同一个数轴上表示不等式①和②的解集:
∴原不等式组的解集为4<x<10 .
①
②
例1 解不等式组: .
①
②
在同一个数轴上表示不等式①和②的解集:
解:解不等式①,得 .
解不等式②,得 .
∴原不等式组的解集为 .
例2 解不等式组: .
①
②
解不等式②,得 x≥4 .
在同一个数轴上表示不等式①和②的解集:
∴原不等式组的解集为 x≥4 .
解:解不等式①,得 .
例3 用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
因为x只能取整数,所以x=6 .
即有6辆汽车运这批货物.
解:设有x 辆汽车,则这批货物共有(4x+20) t.
依题意得
解不等式组,得5<x<7.
4x+20<8x
4x+20>8(x-1)
例4 一群女生住若干间宿舍,每间住4人,剩19人无房住;每间住6人,有一间宿舍住不满,可能有多少间宿舍,多少名学生
解得: .
解:设有x间宿舍,每间住4人,剩下19人,因此学生人数为(4x+19)人.
根据题意,得 0<4x+19-6(x-1)<6.
因为x是整数,所以x=10,11,12.
因此有三种可能,
第一种,有10间宿舍,59名学生;
第二种,有11间宿舍,63名女生;
第三种,有12间宿舍,67名女生.
随堂练习
1. 不等式组 的最大整数解为( )
A.8 B.6 C.5 D.4
C
2. 如果代数式3x+2与代数式-2x+1的值都大于1,那么x的取值范围是( )
C
A. B. C. D. 不存在
3. 按图所示的程序进行操作,规定:程序运行从“输入一个值x”到“结果是否≥365”为一次操作.如果操作进行4次才能得到输出值,那么输入值x的取值范围是____________.
5≤x<14
4. 解不等式组:
①
②
(1)
解:(1)解不等式①,得x>2.5.
解不等式②,得x≤4.
在数轴上表示不等式①和②的解集,如图,
所以不等式组的解集是2.5<x≤4.
①
②
(2)
(2)解不等式①,得x>2.
解不等式②,得x>4.
在数轴上表示不等式①和②的解集,如图.
所以不等式组的解集是x>4.
5. 把一些书分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人分到的书不足3本.这些书有多少本 学生有多少人
解:设有x名学生,则有(3x+8)本书.
由题意得:0<(3x+8)-5(x-1)<3.
解得5<x<6.5.
因为x是正整数,所以x=6,
所以3x+8=26.
即有6名学生,26本书.
解:设张明平均每天读x页.
6. 一本英语书共98页,张明读了一周(7天)还没读完. 而李永不到一周就读完.李永平均每天比张明多读3页,张明平均每天读多少页(答案取整数)?
由题意得:
解得:11<x<14 .
因为x是整数,
所以x=12,13.
即张明平均每天读12或13页.
7(x+3)>98
7x<98
课堂小结
一元一次不等式组
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
解较复杂的一元一次不等式组
实际问题
不等关系
不等式
不等式组
结合实际因素
找出
列出
组成
求解
解决
谢谢聆听
2.6.1 一元一次不等式组
学习目标
1. 理解一元一次不等式组及其解的意义,加强运算的熟练性和准确性,培养思维的全面性.
2. 初步感知利用一元一次不等式解集的数轴表示求不等式组的解和解集的方法.
知识回顾
左右两边都是整式,只含一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
1. 一元一次不等式的定义
(1)去分母 (注意符号)
(2)去括号
(3)移项
(4)合并同类项
(5)未知数的系数化为1(注意符号)
2. 解一元一次不等式的一般步骤
新课导入
一个长方形足球场的宽为70m,如果它的周长大于350 m,面积小于7560 m2,求这个足球场的长x的取值范围,并判断这个足球场是否可以进行国际足球比赛(注:用于国际比赛的足球场的长在100至110 m之间,宽在64至75 m之间).
解:根据周长大于350 m,得
2(x+70)>350
根据面积小于7560 m2,得
70x<7560
①
②
x需同时满足①和②,你能求出它吗?.
带着这个问题开始今天的学习吧!
某校今年冬季烧煤取暖时间为4个月.如果每月比计划多烧5 t煤,那么取暖用煤总量将超过100 t;如果每月比计划少烧5 t煤,那么取暖用煤总量将不足68 t.
若该校计划每月烧煤x t,则x满足怎样的关系式?
解:根据题意,得
4(x+5)>100, ①
4(x-5)<68. ②
未知数x同时满足①②两个不等式,把①②两个不等式组合在一起,就组成了一个一元一次不等式组,记作
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
4(x+5)>100,
4(x-5)<68.
例1 下列各不等式组,其中是一元一次不等式组的有_________.(填序号)
③④⑤
用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C含量及购买这两种原料的价格如下表所示:
原料 甲 乙
维生素C的含量/(单位/kg) 600 100
原料价格/(元/kg) 8 4
(1)现配制这种饮料10 kg,要求至少含有4200单位的维生素C,试写出所需甲种原料的质量x(kg)应满足的不等式;
600x+100(10-x) ≥ 4200
8x+4(10-x)≤72
(2)如果还要求购买甲、乙两种原料的费用不超过72元,那么你能写出x(kg)应满足的另一个不等式吗?
(3)如果要配制的饮料同时满足两个小题的条件,那么你能列出一个不等式组吗?
你能找出符合这个一元一次不等式组的未知数的值吗?
600x+100(10-x) ≥ 4200
8x+4(10-x)≤72
600x+100(10-x) ≥ 4200
8x+4(10-x)≤72
①
②
解:解不等式①,得
解不等式组:
x≥6.4 .
解不等式②,得
x≤8 .
在同一数轴上表示不等式①②的解集,如下图.
所以原不等式组的解集为:6.4≤x≤8.
公共部分
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集. 求不等式组解集的过程,叫做解不等式组.
例2 解不等式组: .
①
②
解:解不等式①,得 x>2 .
解不等式②,得 x>4 .
在同一个数轴上表示不等式①和②的解集:
∴原不等式组的解集为 x>4 .
例3 解不等式组: .
①
②
解:解不等式①,得 x> .
解不等式②,得 x<5 .
在同一个数轴上表示不等式①和②的解集:
∴原不等式组的解集为 .
随堂练习
1. 下列不等式组中,是一元一次不等式组的是( )
A. B. C. D.
A
2. 已知点A(x+3,2x-4)在第四象限,则x的取值范围是__________.
-3<x<2
3. 不等式组的最小整数解是______.
0
解:(1)解不等式①,得x<1 .
解不等式②,得x<3 .
在数轴上表示不等式①和②的解集:
∴原不等式组的解集为x<1 .
(2)解不等式①,得x>-2.
解不等式②,得x>1.
∴原不等式组的解集为x>1.
4. 解下列不等式组,并把它们的解集在数轴上表示出来:
(1)
(2)
①
②
①
②
在数轴上表示不等式①和②的解集:
5. 解不等式组:
①
②
解:解不等式①,得x<-1 .
解不等式②,得x≥2 .
∴原不等式组无解.
在数轴上表示不等式①和②的解集:
课堂小结
不等式解集的四种情况(a>b)
① 的解集为x>a .
② 的解集为x<b .
③ 的解集为b<x<a.
④ 无解.
大大取大
小小取小
大小小大取中间
大大小小没得找
谢谢聆听
2.6.2 一元一次不等式组
学习目标
1. 会熟练地解复杂的一元一次不等式组.
2. 会根据题意列一元一次不等式组,解决实际问题.
知识回顾
1. 一元一次不等式组
(1)解每一个一元一次不等式;
(2)解集的表示:口诀法或数轴法.
2. 解一元一次不等式组的一般步骤
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
新课导入
在什么条件下,长度为3 cm,7 cm,x cm的三条线段可以围成一个三角形
你和同伴所列的不等式组一样吗 解集呢 与同伴交流.
3+7>x
7-3<x
解:根据三角形任意两边之和大于第三边,三角形任意两边之差小于第三边,得
解不等式①,得 x<10 .
解不等式②,得 x>4 .
在同一个数轴上表示不等式①和②的解集:
∴原不等式组的解集为4<x<10 .
①
②
例1 解不等式组: .
①
②
在同一个数轴上表示不等式①和②的解集:
解:解不等式①,得 .
解不等式②,得 .
∴原不等式组的解集为 .
例2 解不等式组: .
①
②
解不等式②,得 x≥4 .
在同一个数轴上表示不等式①和②的解集:
∴原不等式组的解集为 x≥4 .
解:解不等式①,得 .
例3 用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
因为x只能取整数,所以x=6 .
即有6辆汽车运这批货物.
解:设有x 辆汽车,则这批货物共有(4x+20) t.
依题意得
解不等式组,得5<x<7.
4x+20<8x
4x+20>8(x-1)
例4 一群女生住若干间宿舍,每间住4人,剩19人无房住;每间住6人,有一间宿舍住不满,可能有多少间宿舍,多少名学生
解得: .
解:设有x间宿舍,每间住4人,剩下19人,因此学生人数为(4x+19)人.
根据题意,得 0<4x+19-6(x-1)<6.
因为x是整数,所以x=10,11,12.
因此有三种可能,
第一种,有10间宿舍,59名学生;
第二种,有11间宿舍,63名女生;
第三种,有12间宿舍,67名女生.
随堂练习
1. 不等式组 的最大整数解为( )
A.8 B.6 C.5 D.4
C
2. 如果代数式3x+2与代数式-2x+1的值都大于1,那么x的取值范围是( )
C
A. B. C. D. 不存在
3. 按图所示的程序进行操作,规定:程序运行从“输入一个值x”到“结果是否≥365”为一次操作.如果操作进行4次才能得到输出值,那么输入值x的取值范围是____________.
5≤x<14
4. 解不等式组:
①
②
(1)
解:(1)解不等式①,得x>2.5.
解不等式②,得x≤4.
在数轴上表示不等式①和②的解集,如图,
所以不等式组的解集是2.5<x≤4.
①
②
(2)
(2)解不等式①,得x>2.
解不等式②,得x>4.
在数轴上表示不等式①和②的解集,如图.
所以不等式组的解集是x>4.
5. 把一些书分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人分到的书不足3本.这些书有多少本 学生有多少人
解:设有x名学生,则有(3x+8)本书.
由题意得:0<(3x+8)-5(x-1)<3.
解得5<x<6.5.
因为x是正整数,所以x=6,
所以3x+8=26.
即有6名学生,26本书.
解:设张明平均每天读x页.
6. 一本英语书共98页,张明读了一周(7天)还没读完. 而李永不到一周就读完.李永平均每天比张明多读3页,张明平均每天读多少页(答案取整数)?
由题意得:
解得:11<x<14 .
因为x是整数,
所以x=12,13.
即张明平均每天读12或13页.
7(x+3)>98
7x<98
课堂小结
一元一次不等式组
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
解较复杂的一元一次不等式组
实际问题
不等关系
不等式
不等式组
结合实际因素
找出
列出
组成
求解
解决
谢谢聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
