2021-2022学年人教版七年级数学下册5.1.3同位角、内错角、同旁内角课件(19张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.1.3同位角、内错角、同旁内角课件(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 18:21:06 | ||
图片预览





文档简介
(共19张PPT)
5.1.3 同位角、内错角、同旁内角
5.1 相交线
5.1.3 同位角、内错角、同旁内角
能在具体图形中判断同位角、内错角、同旁同内角.
从分解过程中,体会化繁为简,化难为易的化归思想
【学习目标】
复习旧知
(1)找出图中的邻补角、对顶角,并说出他们的共同点.
(2)若再增加一条直线 c,还会得出些什么角?
问题:如画直线 a,b 相交于点O.解决以下问题.
a
b
c
①两条直线相交而成的角;
③成对出现的
②一个公共顶点
邻补角与对顶角的共同点.
新知探究
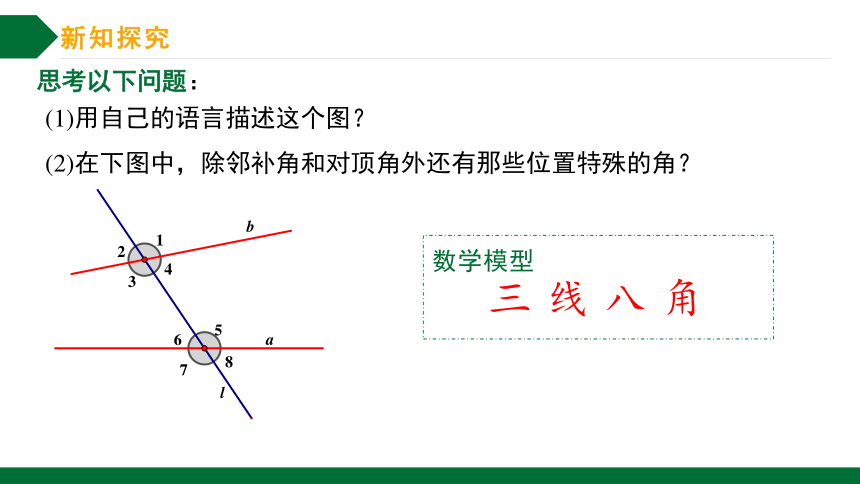
思考以下问题:
(1)用自己的语言描述这个图?
(2)在下图中,除邻补角和对顶角外还有那些位置特殊的角?
三线八角
数学模型
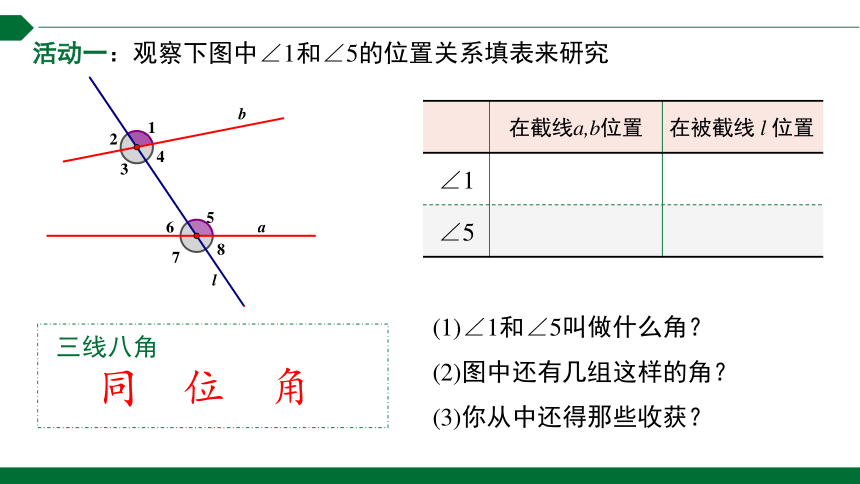
活动一:观察下图中∠1和∠5的位置关系填表来研究
(1)∠1和∠5叫做什么角?
(2)图中还有几组这样的角?
(3)你从中还得那些收获?
在截线a,b位置 在被截线 l 位置
∠1
∠5
三线八角
同位角
1.下列图形中,∠1和∠2是同位角的有( )
针对练习
A
A.(1),(2) B.(3),(4) C.(1),(2),(3) D.(2),(3) ,(3)
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
一般的三线八角中,有4组同位角,形如“F”
同位角
活动二:观察下图中∠3和∠5的位置关系填表来研究
(1)∠3和∠5叫做什么角?
(2)图中还有几组这样的角?
(3)你从中还得那些收获?
在截线a,b位置 在被截线 l 位置
∠3
∠5
三线八角
内错角
活动三:观察下图中∠4和∠5的位置关系填表来研究
(1)∠4和∠5叫做什么角?
(2)图中还有几组这样的角?
(3)你从中还得那些收获?
在截线a,b位置 在被截线 l 位置
∠4
∠5
三线八角
同旁内角
针对练习
一般的三线八角中,有2组内错角,形如“Z”
内错角
2 、如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
D
针对练习
一般的三线八角中,有2组内错角,形如“U”
同旁内角
3、下列图形中,∠1和∠2是同旁内角的有( )
A
B
C
D
1
2
1
2
1
2
1
2
A
典例讲解
例1. 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
例2 如图,直线DE,BC被直线AB所截. (教材P7)
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗? 为什么?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1与∠2是内错角,
∠1和∠3同旁内角,
∠1和∠4是同位角.
例5 如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗? 为什么?
4
3
2
1
F
E
D
C
B
A
解:(2)∵ ∠1=∠4(已知),
∴ ∠2=∠4(对顶角相等),
∴ ∠1=∠2(等量代换).
∵ ∠4+∠3=180°(邻补角的定义),
∴ ∠1+∠3=180°,
即∠1与∠3互补.
课堂小结
特殊:∠1=90°
a
b
O
1
a
b
O
a
b
l
a⊥b.
增加一直线
三线八角
特殊
图形 基本图 特征 组数
同位角
内错角
同旁内角
F
Z
U
三线八角
4 组
2 组
2 组
巩固练习
1、如图①,在所标识的角中,同位角是( )
A.∠1和∠2 B.∠1和∠3 C.∠1和∠4 D.∠2和∠3
C
2、如图②,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
D
3、如图③,与∠1是同旁内角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
D
图①
图②
图③
4、下列图形中(如图),∠1和∠2是同位角的有( )
A.1个 B.2个 C.3个 D.4个
D
5、如图,与∠1互为同旁内角的角共有( )个.
A.1 B.2
C.3 D.4
C
6、如图,下列说法正确的是( )
A.∠2和∠B是同位角 B.∠2和∠B是内错角
C.∠1和∠A是内错角 D.∠3和∠B是同旁内角
D
7、如图,找出图中所能表示的角中所有与∠1是同位角有__________________,与∠1内错角______________,
与∠1同旁内角___________________.
∠6,∠7,∠ABC.
没有同位角
∠2
5.1.3 同位角、内错角、同旁内角
5.1 相交线
5.1.3 同位角、内错角、同旁内角
能在具体图形中判断同位角、内错角、同旁同内角.
从分解过程中,体会化繁为简,化难为易的化归思想
【学习目标】
复习旧知
(1)找出图中的邻补角、对顶角,并说出他们的共同点.
(2)若再增加一条直线 c,还会得出些什么角?
问题:如画直线 a,b 相交于点O.解决以下问题.
a
b
c
①两条直线相交而成的角;
③成对出现的
②一个公共顶点
邻补角与对顶角的共同点.
新知探究
思考以下问题:
(1)用自己的语言描述这个图?
(2)在下图中,除邻补角和对顶角外还有那些位置特殊的角?
三线八角
数学模型
活动一:观察下图中∠1和∠5的位置关系填表来研究
(1)∠1和∠5叫做什么角?
(2)图中还有几组这样的角?
(3)你从中还得那些收获?
在截线a,b位置 在被截线 l 位置
∠1
∠5
三线八角
同位角
1.下列图形中,∠1和∠2是同位角的有( )
针对练习
A
A.(1),(2) B.(3),(4) C.(1),(2),(3) D.(2),(3) ,(3)
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
一般的三线八角中,有4组同位角,形如“F”
同位角
活动二:观察下图中∠3和∠5的位置关系填表来研究
(1)∠3和∠5叫做什么角?
(2)图中还有几组这样的角?
(3)你从中还得那些收获?
在截线a,b位置 在被截线 l 位置
∠3
∠5
三线八角
内错角
活动三:观察下图中∠4和∠5的位置关系填表来研究
(1)∠4和∠5叫做什么角?
(2)图中还有几组这样的角?
(3)你从中还得那些收获?
在截线a,b位置 在被截线 l 位置
∠4
∠5
三线八角
同旁内角
针对练习
一般的三线八角中,有2组内错角,形如“Z”
内错角
2 、如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
D
针对练习
一般的三线八角中,有2组内错角,形如“U”
同旁内角
3、下列图形中,∠1和∠2是同旁内角的有( )
A
B
C
D
1
2
1
2
1
2
1
2
A
典例讲解
例1. 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
例2 如图,直线DE,BC被直线AB所截. (教材P7)
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗? 为什么?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1与∠2是内错角,
∠1和∠3同旁内角,
∠1和∠4是同位角.
例5 如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗? 为什么?
4
3
2
1
F
E
D
C
B
A
解:(2)∵ ∠1=∠4(已知),
∴ ∠2=∠4(对顶角相等),
∴ ∠1=∠2(等量代换).
∵ ∠4+∠3=180°(邻补角的定义),
∴ ∠1+∠3=180°,
即∠1与∠3互补.
课堂小结
特殊:∠1=90°
a
b
O
1
a
b
O
a
b
l
a⊥b.
增加一直线
三线八角
特殊
图形 基本图 特征 组数
同位角
内错角
同旁内角
F
Z
U
三线八角
4 组
2 组
2 组
巩固练习
1、如图①,在所标识的角中,同位角是( )
A.∠1和∠2 B.∠1和∠3 C.∠1和∠4 D.∠2和∠3
C
2、如图②,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
D
3、如图③,与∠1是同旁内角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
D
图①
图②
图③
4、下列图形中(如图),∠1和∠2是同位角的有( )
A.1个 B.2个 C.3个 D.4个
D
5、如图,与∠1互为同旁内角的角共有( )个.
A.1 B.2
C.3 D.4
C
6、如图,下列说法正确的是( )
A.∠2和∠B是同位角 B.∠2和∠B是内错角
C.∠1和∠A是内错角 D.∠3和∠B是同旁内角
D
7、如图,找出图中所能表示的角中所有与∠1是同位角有__________________,与∠1内错角______________,
与∠1同旁内角___________________.
∠6,∠7,∠ABC.
没有同位角
∠2
