2021-2022学年北师大版数学八年级下册1.1等腰三角形课件(22张)
文档属性
| 名称 | 2021-2022学年北师大版数学八年级下册1.1等腰三角形课件(22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 18:33:40 | ||
图片预览






文档简介
1.1 等腰三角形
学习目标
1. 进一步了解“8条基本事实”,学会证明的基本步骤和书写格式.
2. 能证明“AAS”这一全等的判定定理,能利用全等三角形的性
质去证明等腰三角形的有关性质定理及其推论.
3. 灵活运用等腰三角形的性质进行计算和证明.
新课导入
1. 两点确定一条直线.
2. 两点之间线段最短.
3. 同一平面内,过一点有且只有一条直线与已知直线垂直.
4. 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
5. 过直线外一点有且只有一条直线与这条直线平行 .
6. 两边及其夹角分别相等的两个三角形全等(SAS).
7. 两角及其夹边分别相等的两个三角形全等(ASA).
8. 三边对应相等的两个三角形全等(SSS).
复习回顾已有的事实(公理),你还记得她们吗?
新课导入
想一想:在探索三角形全等的条件时,我们已经探索过“两角分别对应相等且其中一组等角的对边相等的两个三角形全等”这一结论,你能用已有的基本事实和定理证明这一结论吗?
聪明如我的你们
一定可以搞定哦!
画图试试!
注意对于一个命题的证明,需要哪三部曲呢?
A
B
C
A1
B1
C1
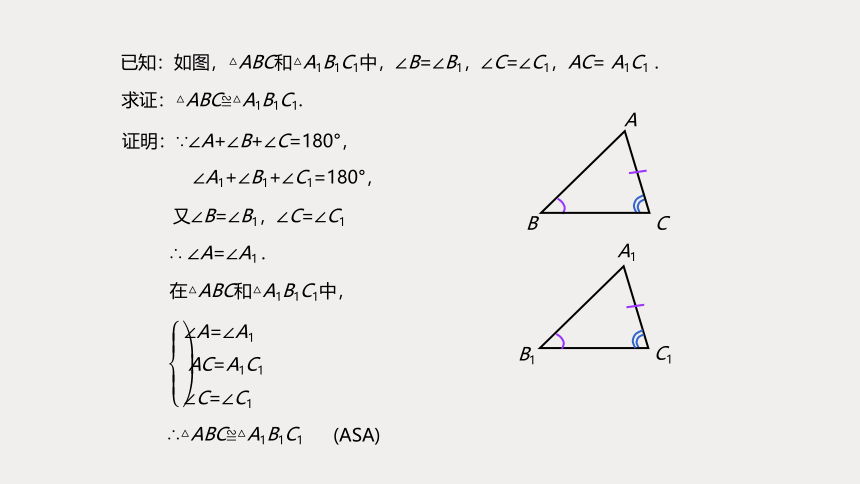
已知:如图,△ABC和△A1B1C1中,∠B=∠B1,∠C=∠C1,AC= A1C1 .
求证:△ABC≌△A1B1C1.
证明:∵∠A+∠B+∠C=180°,
∠A1+∠B1+∠C1=180°,
又∠B=∠B1,∠C=∠C1
∴ ∠A=∠A1 .
在△ABC和△A1B1C1中,
∴△ABC≌△A1B1C1
(ASA)
∠A=∠A1
AC=A1C1
∠C=∠C1
?????
?
定理:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
(AAS)
根据全等三角形的定义可得:
全等三角形对应边相等,对应角相等.
你还记得我们探索过的等腰三角形的性质吗?
推论:等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).
定理:等腰三角形的两底角相等.(等边对等角)
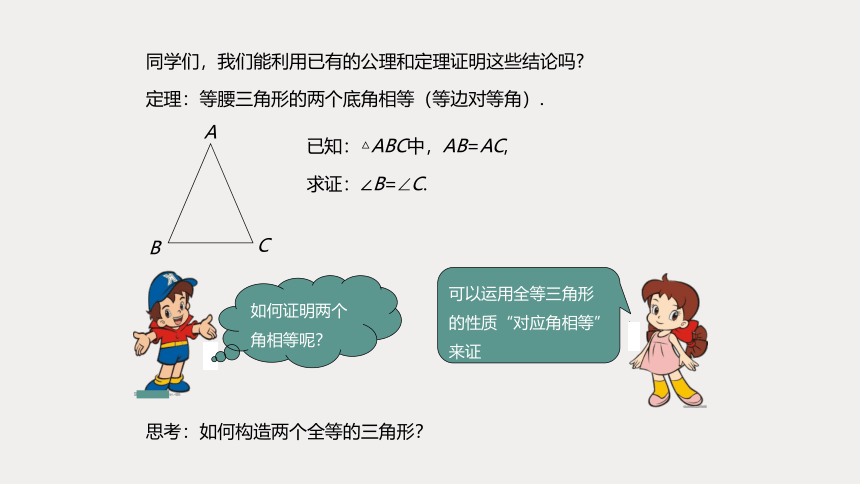
同学们,我们能利用已有的公理和定理证明这些结论吗?
A
B
C
已知:△ABC中,AB=AC,
求证:∠B=?C.
思考:如何构造两个全等的三角形?
定理:等腰三角形的两个底角相等(等边对等角).
如何证明两个角相等呢?
可以运用全等三角形的性质“对应角相等”来证
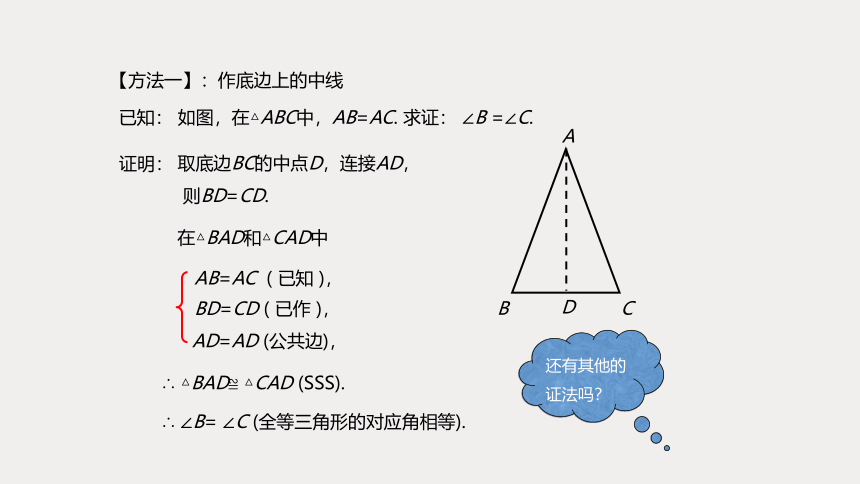
已知: 如图,在△ABC中,AB=AC. 求证: ∠B =∠C.
A
B
C
D
证明:
取底边BC的中点D,连接AD,
则BD=CD.
AB=AC ( 已知 ),
BD=CD ( 已作 ),
AD=AD (公共边),
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
【方法一】:作底边上的中线
还有其他的证法吗?
已知: 如图,在△ABC中,AB=AC. 求证: ∠B =∠C.
A
B
C
D
证明:
作顶角的平分线AD,
则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
【方法二】:作顶角的平分线
在△BAD和△CAD中
想一想:由△BAD≌ △CAD,除了可以得到∠B =∠C之外,你还可以得到哪些相等的线段和相等的角?
解:∵ △BAD≌ △CAD,
∴BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90° .
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
A
B
C
D
定理:等腰三角形的两底角相等(等边对等角).
A
C
B
如图,在△ABC中,
∵ AB=AC(已知),
∴ ∠B=∠C(等边对等角).
总结归纳
A
C
B
D
1
2
∵ AB=AC, ∠1=∠2(已知),
∴ BD=CD,AD⊥BC(三线合一).
∵ AB=AC, BD=CD (已知),
∴ ∠1=∠2,AD⊥BC(三线合一).
∵ AB=AC,AD⊥BC(已知),
∴ BD=CD,∠1=∠2(三线合一).
如图,在△ABC中,
推论:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,
求△ABC各角的度数.
(1)图中相等的角共( )对;
∠A=∠ABD,
∠C=∠BDC=∠ABC;
A. 3对 B. 4对 C. 5对 D. 6对
D
A
B
C
D
x
2x
2x
(2)设∠A=x,请把△ABC的内角和用含 x 的式子表示出来.
∵ ∠A+ ∠ABC+ ∠C=180 °,
∴ x+2x+2x=180 °.
x
x
解:∵AB=AC,BD=BC=AD,
∴ ∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x .
从而∠ABC= ∠C= ∠BDC=2x .
∴∠A+∠ABC+∠C=x+2x+2x=180°.
解得x=36°.
在含多个等腰三角形的图形中求角时,常常利用方程思想,通过内角、外角之间的关系进行转化求解.
归纳
∴∠A=36°,∠ABC=∠C=72°.
A
B
C
D
x
2x
2x
x
x
例2 已知:如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、∠CAD的度数.
解:在△ABC中,
∵AB=AC,
∴∠B=∠C(等边对等角).
∴∠B=∠C = 12 (180°-∠BAC)
?
= 40°
∵AD⊥BC,
∴∠BAD=∠CAD =50°(三线合一).
A
B
D
C
例3 如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=28°,且AD=AE,
求∠EDC的度数.
解:∵AB=AC,AD⊥BC,
∴∠DAE=∠BAD=28°.
∵AD=AE,
∴∠ADE = 12 ×(180°-∠DAE)?= 12?×( 180° - 28°)?=76°.
∴∠EDC=90° -∠ADE=90°-76°=14°.
?
随堂练习
1. 等腰三角形一个底角为70°,它的顶角为______.
2. 等腰三角形一个角为70°,它的另外两个角为_________________________.
3. 等腰三角形一个角为110°,它的另外两个角为______________.
① 顶角+2×底角=180°
② 顶角=180°?2×底角
?
③ 底角=(180°?顶角)÷2
?
④0°< 顶角 < 180°
【结论】:在等腰三角形中,
40 °
35 °,35 °
70°,40°或55°,55°
⑤0° < 底角 < 90°
4. 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=40°.
求:(1)∠ADC的大小;
(2)∠BAD的大小.
解:(1)∵AB=AC,D是BC边上的中点,
∴AD⊥BC .
即∠ADC=90°;
(2)∵∠B=40°,
∴∠BAD=50°.
5. 如图,在△ABC中,AB=BC=AD,BD=CD,求∠ABC的度数.
解:∵BD=CD,
∴∠BCD=∠CBD.
设∠BCD=∠CBD=x.
∵AB=BC=AD,
∴∠ABD=∠ADB=∠BCD+∠CBD=2x,∠A=∠C=x.
∴∠ABC=3x.
∵∠A+∠ABC+∠C=180°,
∴5x=180° .
解得x=36° .
∴∠ABC=108°.
6. 已知:如图,在△ABC中,AB=AD=DC,∠BAD=30°.
试求∠B和∠C的度数.
解:∵AB=AD=DC,
∴在△ABD中,
∠B=∠ADB=12 ×(180°-30°)=75° .
∵AD=DC,
∴在△ADC中,∠C=12×∠ADB=37.5°.
∴∠B=75°,∠C=37.5°.
?
课堂小结
等腰三角形的性质
等边对等角
三线合一
等腰三角形的两个底角相等
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.
数学思想:分类讨论
学习目标
1. 进一步了解“8条基本事实”,学会证明的基本步骤和书写格式.
2. 能证明“AAS”这一全等的判定定理,能利用全等三角形的性
质去证明等腰三角形的有关性质定理及其推论.
3. 灵活运用等腰三角形的性质进行计算和证明.
新课导入
1. 两点确定一条直线.
2. 两点之间线段最短.
3. 同一平面内,过一点有且只有一条直线与已知直线垂直.
4. 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
5. 过直线外一点有且只有一条直线与这条直线平行 .
6. 两边及其夹角分别相等的两个三角形全等(SAS).
7. 两角及其夹边分别相等的两个三角形全等(ASA).
8. 三边对应相等的两个三角形全等(SSS).
复习回顾已有的事实(公理),你还记得她们吗?
新课导入
想一想:在探索三角形全等的条件时,我们已经探索过“两角分别对应相等且其中一组等角的对边相等的两个三角形全等”这一结论,你能用已有的基本事实和定理证明这一结论吗?
聪明如我的你们
一定可以搞定哦!
画图试试!
注意对于一个命题的证明,需要哪三部曲呢?
A
B
C
A1
B1
C1
已知:如图,△ABC和△A1B1C1中,∠B=∠B1,∠C=∠C1,AC= A1C1 .
求证:△ABC≌△A1B1C1.
证明:∵∠A+∠B+∠C=180°,
∠A1+∠B1+∠C1=180°,
又∠B=∠B1,∠C=∠C1
∴ ∠A=∠A1 .
在△ABC和△A1B1C1中,
∴△ABC≌△A1B1C1
(ASA)
∠A=∠A1
AC=A1C1
∠C=∠C1
?????
?
定理:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
(AAS)
根据全等三角形的定义可得:
全等三角形对应边相等,对应角相等.
你还记得我们探索过的等腰三角形的性质吗?
推论:等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).
定理:等腰三角形的两底角相等.(等边对等角)
同学们,我们能利用已有的公理和定理证明这些结论吗?
A
B
C
已知:△ABC中,AB=AC,
求证:∠B=?C.
思考:如何构造两个全等的三角形?
定理:等腰三角形的两个底角相等(等边对等角).
如何证明两个角相等呢?
可以运用全等三角形的性质“对应角相等”来证
已知: 如图,在△ABC中,AB=AC. 求证: ∠B =∠C.
A
B
C
D
证明:
取底边BC的中点D,连接AD,
则BD=CD.
AB=AC ( 已知 ),
BD=CD ( 已作 ),
AD=AD (公共边),
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
【方法一】:作底边上的中线
还有其他的证法吗?
已知: 如图,在△ABC中,AB=AC. 求证: ∠B =∠C.
A
B
C
D
证明:
作顶角的平分线AD,
则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
【方法二】:作顶角的平分线
在△BAD和△CAD中
想一想:由△BAD≌ △CAD,除了可以得到∠B =∠C之外,你还可以得到哪些相等的线段和相等的角?
解:∵ △BAD≌ △CAD,
∴BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90° .
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
A
B
C
D
定理:等腰三角形的两底角相等(等边对等角).
A
C
B
如图,在△ABC中,
∵ AB=AC(已知),
∴ ∠B=∠C(等边对等角).
总结归纳
A
C
B
D
1
2
∵ AB=AC, ∠1=∠2(已知),
∴ BD=CD,AD⊥BC(三线合一).
∵ AB=AC, BD=CD (已知),
∴ ∠1=∠2,AD⊥BC(三线合一).
∵ AB=AC,AD⊥BC(已知),
∴ BD=CD,∠1=∠2(三线合一).
如图,在△ABC中,
推论:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,
求△ABC各角的度数.
(1)图中相等的角共( )对;
∠A=∠ABD,
∠C=∠BDC=∠ABC;
A. 3对 B. 4对 C. 5对 D. 6对
D
A
B
C
D
x
2x
2x
(2)设∠A=x,请把△ABC的内角和用含 x 的式子表示出来.
∵ ∠A+ ∠ABC+ ∠C=180 °,
∴ x+2x+2x=180 °.
x
x
解:∵AB=AC,BD=BC=AD,
∴ ∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x .
从而∠ABC= ∠C= ∠BDC=2x .
∴∠A+∠ABC+∠C=x+2x+2x=180°.
解得x=36°.
在含多个等腰三角形的图形中求角时,常常利用方程思想,通过内角、外角之间的关系进行转化求解.
归纳
∴∠A=36°,∠ABC=∠C=72°.
A
B
C
D
x
2x
2x
x
x
例2 已知:如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、∠CAD的度数.
解:在△ABC中,
∵AB=AC,
∴∠B=∠C(等边对等角).
∴∠B=∠C = 12 (180°-∠BAC)
?
= 40°
∵AD⊥BC,
∴∠BAD=∠CAD =50°(三线合一).
A
B
D
C
例3 如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=28°,且AD=AE,
求∠EDC的度数.
解:∵AB=AC,AD⊥BC,
∴∠DAE=∠BAD=28°.
∵AD=AE,
∴∠ADE = 12 ×(180°-∠DAE)?= 12?×( 180° - 28°)?=76°.
∴∠EDC=90° -∠ADE=90°-76°=14°.
?
随堂练习
1. 等腰三角形一个底角为70°,它的顶角为______.
2. 等腰三角形一个角为70°,它的另外两个角为_________________________.
3. 等腰三角形一个角为110°,它的另外两个角为______________.
① 顶角+2×底角=180°
② 顶角=180°?2×底角
?
③ 底角=(180°?顶角)÷2
?
④0°< 顶角 < 180°
【结论】:在等腰三角形中,
40 °
35 °,35 °
70°,40°或55°,55°
⑤0° < 底角 < 90°
4. 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=40°.
求:(1)∠ADC的大小;
(2)∠BAD的大小.
解:(1)∵AB=AC,D是BC边上的中点,
∴AD⊥BC .
即∠ADC=90°;
(2)∵∠B=40°,
∴∠BAD=50°.
5. 如图,在△ABC中,AB=BC=AD,BD=CD,求∠ABC的度数.
解:∵BD=CD,
∴∠BCD=∠CBD.
设∠BCD=∠CBD=x.
∵AB=BC=AD,
∴∠ABD=∠ADB=∠BCD+∠CBD=2x,∠A=∠C=x.
∴∠ABC=3x.
∵∠A+∠ABC+∠C=180°,
∴5x=180° .
解得x=36° .
∴∠ABC=108°.
6. 已知:如图,在△ABC中,AB=AD=DC,∠BAD=30°.
试求∠B和∠C的度数.
解:∵AB=AD=DC,
∴在△ABD中,
∠B=∠ADB=12 ×(180°-30°)=75° .
∵AD=DC,
∴在△ADC中,∠C=12×∠ADB=37.5°.
∴∠B=75°,∠C=37.5°.
?
课堂小结
等腰三角形的性质
等边对等角
三线合一
等腰三角形的两个底角相等
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.
数学思想:分类讨论
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
