2021-2022学年华东师大版八年级数学下册16.4.1零指数幂与负整数指数幂课件(17张)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学下册16.4.1零指数幂与负整数指数幂课件(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 414.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第16章 分式
16.4.1 零指数幂与负整数指数幂
认真思考 积极主动
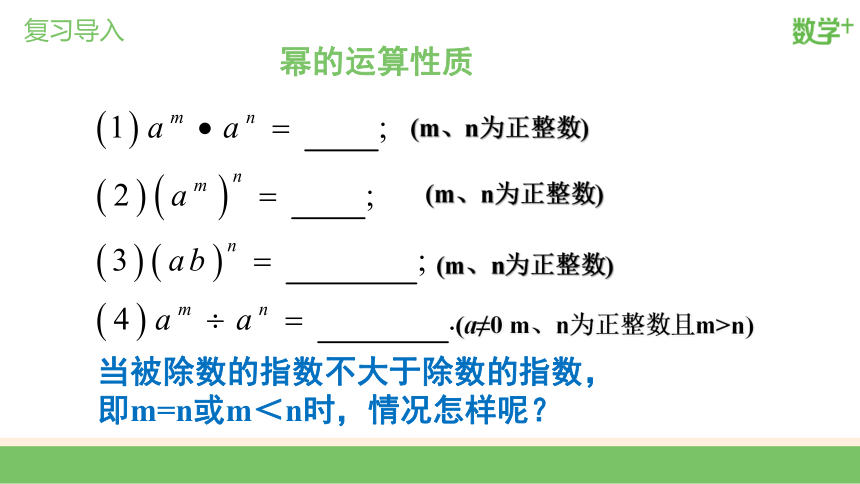
幂的运算性质
(m、n为正整数)
(m、n为正整数)
(m、n为正整数)
(a≠0 m、n为正整数且m>n)
复习导入
当被除数的指数不大于除数的指数,
即m=n或m<n时,情况怎样呢?
学习目标
零整数幂和负整数指数幂的意义;
科学计数法的应用。
新课探究
1.被除数的指数等于除数的指数的情况:
①仿照同底数幂的除法公式来计算,则
②由除法的意义可知,则
新课探究
任何不等于零的数的零次幂等于1.
零的零次幂
没有意义!
一.零指数幂的意义
1.判断题:
×
√
√
√
√
×
( )
( )
( )
( )
( )
( )
随堂练习
1
-1
1
1
无意义
8
0
3.(x-2020)0=1成立的条件是 .
4.当x 时,(x+5)0无意义.
随堂练习
新课探究
2.被除数的指数小于除数的指数的情况:
①仿照同底数幂的除法公式来计算,则
②由约分可知,则
新课探究
二.负整数指数幂的意义
任何不等于零的数的-n (n为正整数)次幂,等于这个数的n 次幂的倒数.
例1 计算:
例题讲解
例2 用小数表示下列各数:
例题讲解
课本20页第1题
牛刀小试
新课探究
三.幂的运算性质
(m、n为正整数)
(m、n为正整数)
(m、n为正整数)
(a≠0 m、n为正整数且m>n)
零指数幂和负整数幂是否符合运算性质?m,n只是整数可以吗?
新课探究
例如:取m=2,n=-3.检验性质1:
所以,性质1成立。
类似地,我们可以检验幂的其他运算性质的正确性。
你有哪些收获?
课堂小结
你有哪些疑惑?
课后作业
书本第21页1,2。
认真作业 勇于探索
下课啦
第16章 分式
16.4.1 零指数幂与负整数指数幂
认真思考 积极主动
幂的运算性质
(m、n为正整数)
(m、n为正整数)
(m、n为正整数)
(a≠0 m、n为正整数且m>n)
复习导入
当被除数的指数不大于除数的指数,
即m=n或m<n时,情况怎样呢?
学习目标
零整数幂和负整数指数幂的意义;
科学计数法的应用。
新课探究
1.被除数的指数等于除数的指数的情况:
①仿照同底数幂的除法公式来计算,则
②由除法的意义可知,则
新课探究
任何不等于零的数的零次幂等于1.
零的零次幂
没有意义!
一.零指数幂的意义
1.判断题:
×
√
√
√
√
×
( )
( )
( )
( )
( )
( )
随堂练习
1
-1
1
1
无意义
8
0
3.(x-2020)0=1成立的条件是 .
4.当x 时,(x+5)0无意义.
随堂练习
新课探究
2.被除数的指数小于除数的指数的情况:
①仿照同底数幂的除法公式来计算,则
②由约分可知,则
新课探究
二.负整数指数幂的意义
任何不等于零的数的-n (n为正整数)次幂,等于这个数的n 次幂的倒数.
例1 计算:
例题讲解
例2 用小数表示下列各数:
例题讲解
课本20页第1题
牛刀小试
新课探究
三.幂的运算性质
(m、n为正整数)
(m、n为正整数)
(m、n为正整数)
(a≠0 m、n为正整数且m>n)
零指数幂和负整数幂是否符合运算性质?m,n只是整数可以吗?
新课探究
例如:取m=2,n=-3.检验性质1:
所以,性质1成立。
类似地,我们可以检验幂的其他运算性质的正确性。
你有哪些收获?
课堂小结
你有哪些疑惑?
课后作业
书本第21页1,2。
认真作业 勇于探索
下课啦
