2021-2022学年人教版七年级数学下册5.1.2垂线(2)课件(14张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.1.2垂线(2)课件(14张) |
|
|
| 格式 | pptx | ||
| 文件大小 | 256.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
5.1.2 垂 线
5.1 相交线
( 第 2 课时 )
5.1.2 垂 线
会用垂直性质来说理.
能用垂线段最短解决实际问题.
能量直线外一点到直线的距离.
【学习目标】
( 第 2 课时 )
新知探究
(1)你所画的直线是垂直于直线 l 吗?为什么?
(2)过直线l上的一点 P 画l的垂线,这样的垂线能画几条
(3)从作图过程中,你得出什么结论
.P
l
问题:如下图过点 P 画直线 l 的垂线。
P
l
.
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.(教材P5)
问题:从垂线的性质你想到了哪些问题?
(1)“在同一平面内”可以去掉吗,请举例说明。
(2)“过一点”中的点与直线有些什么情况?
(3)结合之前所学知识,你怎样理解“有且只有”的意思
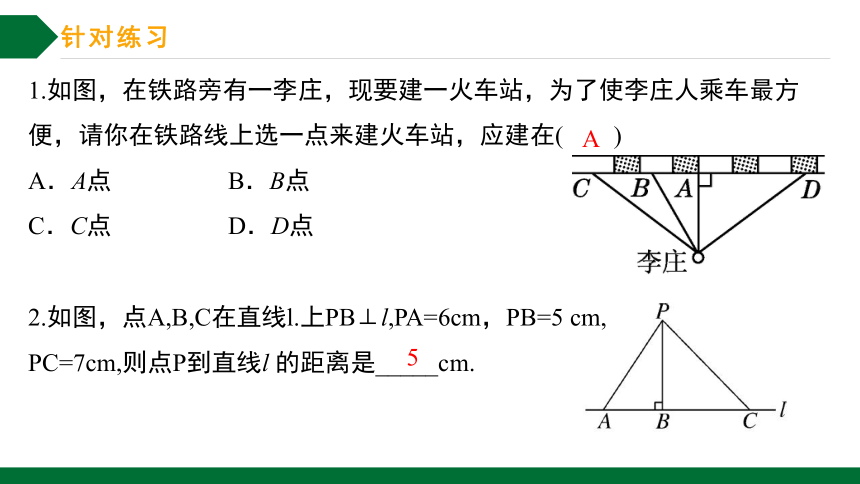
如图,连接直线 l 外一点A与直线上各点的线段.
思考下列问题:
(1) 线段AB, AC, AD , AE谁最短?
(2) 请用自己的句话表示这个结论吗?
(3) 结合线段,你联想到什么结论。
C
D
E
l
B
A
连接直线外一点与直线上各点的所有线段中垂线段最短.
简单说成:垂线段最短.(教材P5)
从直线外一点到这条直线的垂线段的长度叫做这点到直线的距离.(教材P5)
C
D
E
l
B
A
垂线段AD的长度叫做点A到直线 l 的距离.
针对练习
1.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点
C.C点 D.D点
A
2.如图,点A,B,C在直线l.上PB⊥l,PA=6cm,PB=5 cm,
PC=7cm,则点P到直线l 的距离是_____cm.
5
典例讲解
例.如图,码头、火车站分别位于A,B 两点,直线a 和 b分别表示铁路与河流.
(1)从火车站到码头怎样走最近 画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近 画图并说明理由.
课堂小结
①在同一平面内,过一点有且只有一条直线与已知直线垂直.
②垂线段最短.
垂 线
定 义
画法
性质
点到直线的距离
①∵∠AOD=90°,∴AB⊥CD.
②∵ AB⊥CD , ∴ ∠AOD=90° .
三步法(贴、移、画),两类.
A
C
O
B
D
C
D
E
l
B
A
点到这条直线的垂线段的长度
巩固练习
1.在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
C
2.下列说法中,正确的有( )
①过两点有且只有一条直线;②连接两点的线段叫做两点的距离;③两点之间,垂线最短;④若AB=BC,则点B是线段AC的中点.
A.1个 B.2个 C.3个 D.4个
A
3.如图,在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为______cm,点B到直线AC的距离为______cm,点C到直线AB的距离为______cm.
4
3
2.4
4.如图,三角形ABC中,∠C=90°,AC=3,点P可以在直线BC上自由移动,则AP的长不可能是 ( )
A.2.5 B.3 C.4 D.5
A
4.如图, AC⊥BC, ∠CDB=90° ,线段AC、BC、CD中最短的是 ( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
3.如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
C
5.已知三角形ABC中,BC=6,AC=3,CP⊥AB,垂足为P,则CP的长可能是( )
A.2 B.4 C.5 D.7
A
6.点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离( )
A.等于4 cm B.等于2 cm C.小于2 cm D.不大于2 cm
D
5.1.2 垂 线
5.1 相交线
( 第 2 课时 )
5.1.2 垂 线
会用垂直性质来说理.
能用垂线段最短解决实际问题.
能量直线外一点到直线的距离.
【学习目标】
( 第 2 课时 )
新知探究
(1)你所画的直线是垂直于直线 l 吗?为什么?
(2)过直线l上的一点 P 画l的垂线,这样的垂线能画几条
(3)从作图过程中,你得出什么结论
.P
l
问题:如下图过点 P 画直线 l 的垂线。
P
l
.
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.(教材P5)
问题:从垂线的性质你想到了哪些问题?
(1)“在同一平面内”可以去掉吗,请举例说明。
(2)“过一点”中的点与直线有些什么情况?
(3)结合之前所学知识,你怎样理解“有且只有”的意思
如图,连接直线 l 外一点A与直线上各点的线段.
思考下列问题:
(1) 线段AB, AC, AD , AE谁最短?
(2) 请用自己的句话表示这个结论吗?
(3) 结合线段,你联想到什么结论。
C
D
E
l
B
A
连接直线外一点与直线上各点的所有线段中垂线段最短.
简单说成:垂线段最短.(教材P5)
从直线外一点到这条直线的垂线段的长度叫做这点到直线的距离.(教材P5)
C
D
E
l
B
A
垂线段AD的长度叫做点A到直线 l 的距离.
针对练习
1.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点
C.C点 D.D点
A
2.如图,点A,B,C在直线l.上PB⊥l,PA=6cm,PB=5 cm,
PC=7cm,则点P到直线l 的距离是_____cm.
5
典例讲解
例.如图,码头、火车站分别位于A,B 两点,直线a 和 b分别表示铁路与河流.
(1)从火车站到码头怎样走最近 画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近 画图并说明理由.
课堂小结
①在同一平面内,过一点有且只有一条直线与已知直线垂直.
②垂线段最短.
垂 线
定 义
画法
性质
点到直线的距离
①∵∠AOD=90°,∴AB⊥CD.
②∵ AB⊥CD , ∴ ∠AOD=90° .
三步法(贴、移、画),两类.
A
C
O
B
D
C
D
E
l
B
A
点到这条直线的垂线段的长度
巩固练习
1.在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
C
2.下列说法中,正确的有( )
①过两点有且只有一条直线;②连接两点的线段叫做两点的距离;③两点之间,垂线最短;④若AB=BC,则点B是线段AC的中点.
A.1个 B.2个 C.3个 D.4个
A
3.如图,在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为______cm,点B到直线AC的距离为______cm,点C到直线AB的距离为______cm.
4
3
2.4
4.如图,三角形ABC中,∠C=90°,AC=3,点P可以在直线BC上自由移动,则AP的长不可能是 ( )
A.2.5 B.3 C.4 D.5
A
4.如图, AC⊥BC, ∠CDB=90° ,线段AC、BC、CD中最短的是 ( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
3.如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
C
5.已知三角形ABC中,BC=6,AC=3,CP⊥AB,垂足为P,则CP的长可能是( )
A.2 B.4 C.5 D.7
A
6.点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离( )
A.等于4 cm B.等于2 cm C.小于2 cm D.不大于2 cm
D
